フーリエ級数展開が自身と一致することの証明：ジョルダン・ルベーグの定理

フーリエ級数展開の係数の求め方はネットに載っていますので, 忘れたときにはお手持ちの端末で検索すれば見つけられますし, 証明を知らなくてもフーリエ級数展開はできます. フーリエ級数展開は実用的な数学操作ですし, 信号解析等に使いたい方は, 証明を省略しても特段問題はないでしょう.

このページは「証明をやらずに公式を使うなんて, そんな横着なことはできない」と考える方向けです.

いざネット上を探してみると, 「フーリエ級数展開が元の関数と一致することの証明」についての解説記事は多くないよう.

ここでは上記内容について, 分かりやすい証明を目指します. ただし1ページで全部やろうとしたので長いです. よろしくお願いします.

マクローリン展開とフーリエ級数展開についての復習

まずは復習からです.

とある関数を \( x^n \) の無限級数で表したものが「マクローリン展開」であり, sin と cos の無限級数で表したものが「フーリエ級数展開」です.

sin関数 と cos関数は周期性を持っているので, フーリエ級数展開で扱われる関数は周期性を持った関数に限定されます.

式で書くと, マクローリン展開, フーリエ級数展開とは, 関数 \( f(x) \) と, 周期 \( 2 \pi \) を持つ関数 \( g(x) \) を, それぞれ

$$ f(x) = \sum_{n=0}^{\infty} A_n x^n $$

$$ g(x) = \frac{a_n}{2} + \sum_{n=1}^{\infty} (a_n \cos{nx} + b_n \sin{nx} ) $$

のように展開することを指します. \( A_n \), \( a_n \), \( b_n \) はそれぞれ各項の係数を表す数列で, 以下になることが知られています.

$$ A_n = \frac{ f^{(n)} (0)}{n!} $$

$$ a_n = \frac{1}{ \pi } \int_{-\pi}^{\pi} f(t) \cos{nt} dt $$

$$ b_n = \frac{1}{ \pi } \int_{-\pi}^{\pi} f(t) \sin{nt} dt $$

マクローリン展開はどんな関数に対しても実行できるわけではなく, 「マクローリン展開が実行できる関数」をちゃんと調べようとすると「テイラーの定理」なるものを導き, その後, 「テイラーの定理が無限大の極限でも成り立つ」ことを示さねばなりません. これについては以下の記事で解説しました.

テイラー展開, マクローリン展開とは何か？

フーリエ級数展開の各項の係数が上の式のように表されることの証明は, マクローリン展開のときよりも複雑です. 次章ではまず, 証明の方向性を述べます.

証明の方針

以下では, フーリエ級数の第\( n \)項までの和 (第\( n \)部分和 \( = S_n \) ) が \( n \rightarrow \infty \) において元の関数 \( f(x) \) に一致することを示します. これが示せれば, フーリエ級数展開が元の関数と一致することの証明となります.

周期 \( 2 \pi \) の区分的に滑らかな連続関数 \( f(x) \) について,

$$ f(x)= \lim_{n \to \infty} S_n (x) $$

が成立することをジョルダン・ルベーグの定理と言います. 即ち, 本記事のゴールはジョルダン・ルベーグの定理を示すことです.

ジョルダン・ルベーグの定理を示すために必要なのが, リーマン・ルベーグの定理です (後述します). また, 式変形を行っていくときには「ディリクレ核」という式を使うとスムーズに式変形ができるので, この「ディリクレ核」についても紹介します.

文字だけではごちゃごちゃして何を言っているかサッパリだと思いますので, 図解しました. 下図をご覧ください.

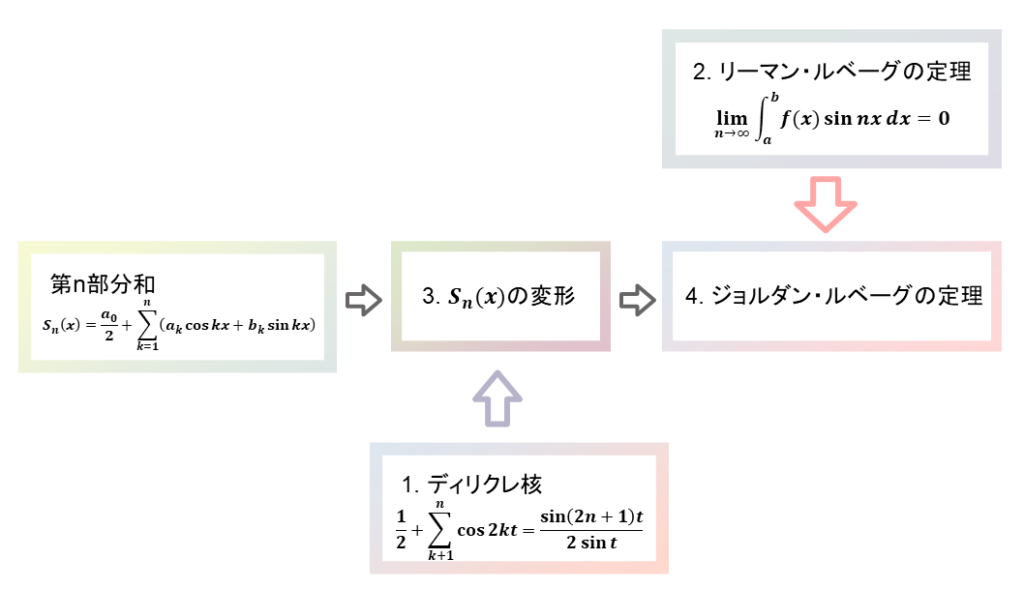
導出フローの図において, 1., 2., . . . と番号を振っています. 以下では, 必要になる語句の解説をした後, この番号の順に証明を進めます.

証明

0. 語句解説

(読み飛ばして頂いて問題ありません. 分からぬ語句がありましたら戻ってきて下さい. また, 以下全て実数で考えていきます.)

・区間 \( [a, b] \)

\( a \) 以上, \( b \) 以下の区間.

・連続, 区分的に連続

連続とは, 関数の図を描いたときに, どこまで拡大しても線が繋がっていることを意味します.

また, 区分的に連続, とは所々途切れている (不連続である)けれども, 途切れている数は有限個である場合を指します.

・不連続点

連続でない点.

なお本記事では, \( x \) が \( f(x) \) の不連続点ならば,

$$ f(x) = \frac{f(x+0) + f(x-0)}{2} $$

と解釈します. \( f(x+0) \) はプラス側から \( x \) に近づけた極限値, \( f(x-0) \) はマイナス側から近づけた極限値です.

・滑らか, 区分的に滑らか

滑らかとは, 関数の図を描いたときに, どこまで拡大してもが線がカクカクしていないことを意味します. 正確に言えば, 「微分可能であること」が「滑らかである」ことと同値で, 「何階連続微分できるか」が「滑らかさ」を指します. 区分的に滑らかである, とは有限個の例外を除いて, 滑らかであることです.

・有界

範囲に限界があること（詳しくは Google先生にお任せします）.

1. ディリクレ核

ディリクレ核とは, 以下の級数を指します.

$$ \frac{1}{2} + \sum_{k=1}^{n} \cos{2kt} $$

このディリクレ核は

$$ \frac{1}{2} + \sum_{k=1}^{n} \cos{2kt} = \frac{ \sin{(2n+1) t } }{2 \sin{t} } \;\;\; \cdots \; (1) $$

と変形することができ, これを使うと後の計算が容易になります. 以下では, 式(1)を帰納法で証明します.

─┘─┘─┘─┘─┘ (証明) ─┘─┘─┘─┘─┘

\( n=1 \) のとき

\begin{eqnarray} (左辺) \times \sin{t} &=& \frac{1}{2} \sin{t} + \cos{2t} \sin{t} \\ &=& \frac{1}{2} \sin{t} + \frac{1}{2} ( \sin{3t} -\sin{t} ) \\ &=& \frac{1}{2} \sin{3t} \end{eqnarray}

となり成立.

\( n=m \) のときに成立すると仮定すると, \( n=m \) のときは,

\begin{eqnarray} &\;& \left( \frac{1}{2} + \sum_{k=1}^{m} \cos{2kt} +\cos{2(m+1)t} \right) \sin{t} \\ &\;& = \frac{1}{2} \sin{(2m+1)t} + \cos{2(m+1)t} \cdot \sin{t} \\ &\;& = \frac{1}{2} \sin{(2m+1)t} + \frac{1}{2} \left\{ \sin{(2m+3)t} -\sin{(2m+1)t} \right\} \\ &\;& = \frac{1}{2} \sin{(2m+3)t} \end{eqnarray}

が得られ, \( n=m+1 \) でも成り立つことが分かる.

よって, 式(1)は成り立つ.

─┘─┘─┘─┘─┘ (証明終了) ─┘─┘─┘─┘─┘

リーマン・ルベーグの定理

次に示すのはリーマン・ルベーグの定理です.

証明してきます.

─┘─┘─┘─┘─┘ (証明) ─┘─┘─┘─┘─┘

\( y= 2 \pi (x-a) / (b-a) \) とおけば, \( x= (b-a) \cdot y \; / \; (2 \pi) +a \) であり,

\begin{eqnarray} &\;& \int_{a}^{b} f(x) \sin{nx} \\ &\;& = \int_{0}^{2 \pi} f \left( \frac{b-a}{2 \pi} y +a \right) \sin{ \left\{ n (\frac{b-a}{2 \pi} y +a ) \right\} } dy \end{eqnarray}

と積分区間が \( [0, 2 \pi ] \) に帰着できるので, 以下では \( [a, b]= [0, 2 \pi ] \) として考える.

また, \( \cos{nx} \) の場合も同様に考えられるので,

$$ \int_{0}^{2 \pi} f(x) \sin{nx} dx \rightarrow 0 \;\; (n \rightarrow \infty) $$

を示せばよい.

積分区間を分割することで,

\begin{eqnarray} &\;& \int_{0}^{2 \pi} f(x) \sin{nx} dx \\ &\;& = \sum_{p=0}^{n-1} \left( \int_{2p \pi /n}^{(2p+1) \pi /n} + \int_{(2p+1) \pi /n}^{2(p+1) \pi /n} \right) f(x) \sin{nx} dx \end{eqnarray}

とみなす.

ここで, \( x= y + \pi /n \) とおいて,

\begin{eqnarray} &\;& \int_{(2p+1) \pi /n}^{2(p+1) \pi /n} f(x) \sin{nx} dx \\ &\;& = \int_{2p \pi /n}^{(2p+1) \pi /n} f \left( y+ \frac{\pi}{n} \right) \sin{(ny + \pi)} dy \\ &\;& = \; – \int_{2p \pi /n}^{(2p+1) \pi /n} f \left( y+ \frac{\pi}{n} \right) \sin{ny} dy \end{eqnarray}

と変形すると,

\begin{eqnarray} &\;& \int_{0}^{2 \pi} f(x) \sin{nx} dx \\ &\;& = \sum_{p=0}^{n-1} \int_{2p \pi /n}^{(2p+1) \pi /n} \left( f(y) -f \left( y+ \frac{\pi}{n} \right) \right\} \sin{ny} dy \end{eqnarray}

となり,

\begin{eqnarray} &\;& \left| f( x ) \sin{nx} dx \right| \\ &\;& \leq \sum_{p=0}^{n-1} \int_{2p \pi /n}^{(2P+1) \pi /n} \left| f(y) – f \left( y+ \frac{\pi}{n} \right) \right| \left| \sin{ny} \right| dy \\ &\;& \leq \int_{0}^{2 \pi} \left| f(y) – f \left( y+ \frac{\pi}{n} \right) \right| dy \end{eqnarray}

を得る.

右辺の積分は \( f(x) \) に不連続点がなければ, 積分 \( \int \) と極限計算 \( \lim \) の交換が可能なので（有界区間上の \( f(x) \) が一様収束するときに交換可能, こちらに詳しく書かれています（外部リンクです））

\begin{eqnarray} &\;& \lim_{n \to \infty} \left| \int_{0}^{2 \pi} f(x) \sin{nx} dx \right| \\ &\;& \leq \lim_{n \to \infty} \int_{0}^{2 \pi} \left| f(y) – f \left( y+ \frac{\pi}{n} \right) \right| dy \\ &\;& = \int_{0}^{2 \pi} \lim_{n \to \infty} \left| f(y) – f \left( y+ \frac{\pi}{n} \right) \right| dy \ & =0 \end{eqnarray}

よって,

$$ \lim_{n \to \infty} \int_{0}^{2 \pi} f(x) \sin{nx} dx = 0 $$

─┘─┘─┘─┘─┘ (証明終了) ─┘─┘─┘─┘─┘

リーマン・ルベーグの証明の流れをおさらいしますと,

1. 考える対象を \( \lim_{n \to \infty} \int_{0}^{2 \pi} f(x) \sin{nx} dx = 0 \) へ変換
2. 積分区間を分割, 変数変換し, 極限値が \( 0 \) である \( f(y) – f \left( y+ \frac{\pi}{n} \right) \) を作る
3. 極限の計算 ( \( \lim_{ \; n \to \infty} \) ) と 積分 ( \( \int_{0}^{2 \pi} \) ) の交換

となります. ここまでが準備段階です.

3. 第n部分和の式変形

実数全体で定義され, 周期 \( 2 \pi \) である区分的に滑らかな関数 \( f(x) \) について, フーリエ級数の第\( n \)部分和 \( S_n \) は, 以下で定義されます.

$$ S_n (x) = \frac{a_0}{2} + \sum_{k=1}^{n} \left( a_k \cos{kx} + b_k \sin{kx} \right) $$

これを後のジョルダン・ルベーグの定理の証明に使いやすいように変形していきます.

まず, \( S_n (x) \) に係数を代入しましょう.

\begin{eqnarray} & S_n (x) = \frac{1}{2 \pi} \int_{- \pi}^{\pi} f(\xi) d \xi \ & + \frac{1}{2 \pi} \sum_{k=1}^{n} \int_{- \pi}^{\pi} f(\xi) \left( \cos{k \xi} \cos{kx} + \sin{k \xi} \sin{kx} \right) d \xi \end{eqnarray}

三角関数の加法定理

$$ \cos{k \xi} \cos{kx} + \sin{k \xi} \sin{kx} = \cos{k(x- \xi )} $$

を使ってまとめます.

$$ S_n (x) = \frac{1}{\pi} \int_{- \pi}^{\pi} f(\xi) \left\{ \frac{1}{2} + \sum_{k=1}^{n} \cos{k(x- \xi )} \right\} d \xi \cdots (2) $$

ここでディリクレ核を用いた変形, 式(1) を使います. 式(1) において, \( t= (x – \xi )/2 \) として, 式(2) に適用すると, 以下の式が得られます.

$$ S_n (x) = \frac{1}{2 \pi} \int_{- \pi}^{\pi} f( \xi ) \frac{\sin{\frac{(2n+1)(x-\xi)}{2} } }{\sin{\frac{x- \xi }{2} } } d \xi \cdots (3) $$

ここで, \( \xi = x + 2 t \) とおくと, 積分の中身が少し綺麗になります.

$$ S_n (x) = \frac{1}{\pi} \int_{-(x+\pi)/2}^{-(x-\pi)/2} f(x+2t) \frac{\sin{(2n+1)t}}{\sin{t}} dt \cdots (4) $$

\( f(x) \) は周期 \( 2 \pi \) の関数なので, \( f(x+ 2t) \) は \( t \) については周期 \( \pi \) の関数です. また,

\begin{eqnarray} \frac{\sin{(2n+1)t}}{\sin{t}} &=& \frac{\sin{(2nt)}\cos{t}}{\sin{t}} + \frac{\cos{(2nt)}\sin{t}}{\sin{t}} \\ &=& \sin{(2nt)} \frac{1}{\tan{t}} + \cos{(2nt)} \end{eqnarray}

であり, \( n \) は自然数なので, \( \sin{(2n+1)t} / \sin{t} \) は \( t \) について周期 \( \pi \). よって, 式(4)の被積分関数の周期は \( \pi \) です. 積分範囲も丁度 \( \pi \) なので, 積分区間を任意にスライドさせても積分結果は同じになります.

$$ S_n (x) = \frac{1}{\pi} \int_{- \pi /2}^{\pi /2} f(x+2t) \frac{\sin{(2n+1)t}}{\sin{t}} dt $$

また, \( t \; \rightarrow \; – t \) と変数変換すると,

\begin{eqnarray} & \int_{- \pi /2}^{0} f(x+2t) \frac{\sin{(2n+1)t}}{\sin{t}} dt \ & = \int_{0}^{\pi /2} f(x-2t) \frac{\sin{(2n+1)t}}{\sin{t}} dt \end{eqnarray}

なので,

$$ S_n (x) = \frac{1}{\pi} \int_{0}^{\pi /2} \left( f(x+2t) – f(x-2t) \right) \frac{\sin{(2n+1) t}}{\sin{t}} dt \cdots (5) $$

と表すことができます.

さらに, ディリクレ核の式(1)より,

\begin{eqnarray} \int_{0}^{2 \pi} \frac{\sin{(2n+1)t}}{\sin{t}} dt &=& \int_{0}^{2 \pi} \left( 1+ 2 \sum_{k=1}^{n} \cos{2kt} \right) dt \\ &=& \frac{\pi}{2} \end{eqnarray}

であることから,

$$ f(x) = \frac{1}{\pi} \int_{0}^{\pi /2} \frac{\sin{(2n+1)t}}{\sin{t}} \left( 2 f(x) \right) \; dt \cdots (6) $$

と表すことができます. 最後に, 式(5)と式(6)より,

\begin{eqnarray} &\;& \pi \left( S_n (x) – f(x) \right) \\ &\;& = \int_{0}^{\pi /2} \frac{\sin{(2n+1)t}}{\sin{t}} \left( f(x+2t) + f(x-2t) – 2 f(x) \right) \; dt \cdots (7) \end{eqnarray}

となり, すべての準備が整いました.

簡単に流れを確認しますと,

1. 三角関数の加法定理を用いて, ディリクレ核を作る
2. ディリクレ核を利用して整理
3. 被積分関数の周期と積分範囲が同じことを使って, 積分区間を変更
4. \( f(x) \) を変形して, \( S_n (x) – f(x) \; \) を作る

といった具合です. では得られた式(7)を無限大に飛ばしましょう.

4. ジョルダン・ルベーグの定理

─┘─┘─┘─┘─┘ (証明) ─┘─┘─┘─┘─┘

式(7)より,

\begin{eqnarray} &\;& \pi \left( S_n (x) – f(x) \right) \\ &\;& = \int_{0}^{\pi /2} \sin{(2n+1)t} \; g(t) dt \cdots (8) \\ &\;& \\ &\;& \left( g(t) = \left( \; f(x+2t) + f(x-2t) – 2 f(x) \; \right) / \sin{t} \right) \end{eqnarray}

ここで \( f(x) \) は実数全体で定義された区分的に滑らかな関数である. \( [0, \pi ] \) で \( g(t) \) が区分的に連続ならば, リーマン・ルベーグの定理より, \( \lim_{ \; n \to \infty} \pi \left( S_n (x) – f(x) \right) = 0 \) が示せるので, 以下では, リーマン・ルベーグの定理を適用するために \( g(t) \) の区分的連続性を調べる. \( g(t) \) は \( t=0 \) で分母が \( 0 \) なので, \( t \rightarrow 0 \) における連続性を調べる必要がある (他の区間では区分的に連続である).

\begin{eqnarray} &\;& \lim_{t \to 0} g(t) \\ &\;& = \lim_{t \to 0} \left( \frac{f(x+t) -f(x)}{\sin{(t/2)}} + \frac{f(x-t) -f(x)}{\sin{(t/2)}} \right) \\ &\;& = \lim_{t \to 0} \left\{ \left( \frac{f(x+t) -f(x)}{t} + \frac{f(x-t) -f(x)}{t} \right) \frac{t/2}{\sin{(t/2)}} \cdot 2 \right\} \end{eqnarray}

ここで, 各項の極限値は

$$ \lim_{t \to 0} \frac{t/2}{\sin{(t/2)}} =1 $$

$$ \lim_{t \to 0} \frac{f(x+t) -f(x)}{t} = f’ (t) | _{ \; t=x} $$

$$ \lim_{t \to 0} \frac{f(x-t) -f(x)}{t} = \; – f’ (t) | _{ \; t=x} $$

となる.

よって, リーマン・ルベーグの定理の適用条件 ( \( t \rightarrow 0 \) における \( g(t) \) が有限値となる条件)は \( f’ (t) | _{ \; t=x} \) が発散しないことであり, これは \( f(x) \) が微分可能であることと同値である.

\( f(x) \) は実数全体で区分的に滑らかなので, \( [0, \pi ] \)で微分可能であり, 式(8)にはリーマン・ルベーグの定理が適用できる. よって,

$$ \lim_{n \to \infty} \left( S_n (x) – f(x) \right) =0 $$

─┘─┘─┘─┘─┘ (証明終了) ─┘─┘─┘─┘─┘

これにて, \( f(x) \) と, \( \lim_{n \to \infty} S_n (x) \) が一致することが分かりました. 細かな条件は付きますが, フーリエ級数展開した多項式は, 確かに元の関数と一致するわけです.

心置きなくフーリエ級数展開を使ってあげてください.

まとめ

ご覧頂きありがとうございました.

2020年に元の記事を書いたのですが, 2022年に見直してみると, 間違いがたくさんあり, 訂正しました.

本記事がフーリエ級数展開に関する理解の一助となれば幸いです.