ここではフーリエ級数展開からフーリエ変換の導出までの流れを概説します. 詳細は各リンクをご参照ください.
フーリエ級数展開
概要
フーリエ級数展開はマクローリン展開と並べて眺めると理解が容易になります.
マクローリン展開は「とある関数を \(x^n\) (\(n\) は整数) の多項式に変換する操作」でした.
\begin{eqnarray} f(x)= \sum_{n=0}^{\infty} \frac{f^{(n)} (0)}{n!} x^n \end{eqnarray}
任意の関数を別の関数の線形和に変換する操作はマクローリン展開だけではありません. 「三角関数の線形和に変換する」ことも可能で, これがフーリエ級数展開です.
$$ f(x) = \frac{a_0}{2} + \sum_{n=1}^{\infty} ( a_n \cos{nx} + b_n \sin{nx} ) $$
$$ a_n = \frac{1}{ \pi } \int_{-\pi}^{\pi} f(t) \cos{nt} dt, \;\;(n=0, 1, 2, 3, \cdots)$$
$$ b_n = \frac{1}{ \pi } \int_{-\pi}^{\pi} f(t) \sin{nt} dt, \;\; (n=0, 1, 2, 3, \cdots) $$
\( a_n \), \( b_n \) は各項の係数であり, それぞれ cos関数と sin関数にくっついているので, \( a_n \) をフーリエ余弦係数, \( b_n \) をフーリエ正弦係数と呼びます.
フーリエ級数展開は三角関数で展開する関係上, 三角関数の持つ周期性に縛られます. 後述する方法で回避できますが, 基本的には「周期 \(2\pi\) の周期関数」でなければ, フーリエ級数展開はできません.
フーリエ級数展開とは何か? (マクローリン展開とのアナロジーでざっくり解説)
証明
上記の係数を決定することで, フーリエ級数展開ができます. 実用上はそれだけで十分なのですが, 証明をせずに公式を使うのは気持ち悪い, という方もいらっしゃるでしょう.
フーリエ級数展開が元の関数と一致することを証明するのは実はかなり大変で, 本サイトでは以下のような流れで証明しました.
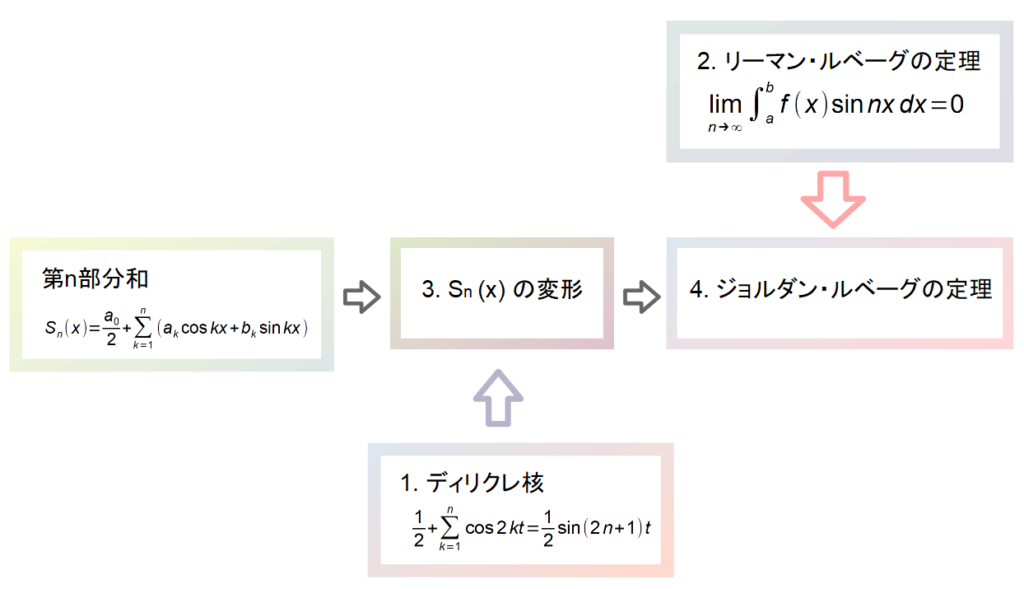
フーリエ級数展開が自身と一致することの証明:ジョルダン・ルベーグの定理
様々なフーリエ級数展開
三角関数は周期性を持つため, 「周期 \(2\pi\) の周期関数」にしか使えない, というルールがあるのですが, 元の関数に手を加えたり, 変数変換をうまく使うことで「非周期関数」や「周期が \(2\pi\) でない関数」においてもフーリエ級数展開ができます.
また, オイラーの公式を使うことで, フーリエ級数展開をもっと綺麗に書くことができます. これを指数関数型の(もしくは, 複素形式の)フーリエ級数展開と呼びます.
指数関数型のフーリエ級数展開を導入する理由は「美の追求」では勿論なく, 後述のフーリエ変換の前準備です.
フーリエの積分公式
フーリエ級数展開は「とある関数を三角関数の無限線形和(級数)に変換する」という操作でした. 級数とは「離散的な値の和」なのですが, 限定的な状況下においては「連続する値の和」で変換することもできます. 「連続する値の和」とは何かというと, それはまさしく「積分」です.
フーリエの積分公式(三角関数型)
\( f(x) \in L^1 (\mathbb{R}) \) かつ, 区分的に滑らかであるとき,
$$ f(x) = \frac{1}{\pi} \int_{0}^{\infty} \bigg( \int_{- \infty}^{ \infty } f( \xi ) \cos{ \omega (x- \xi )} \; d \xi \bigg) d \omega $$
が成り立つ.
「フーリエの積分公式」とは「とある関数を三角関数の積分で表す方法」を指します.
フーリエの積分公式がどうやって導出されるのかは以下の記事をご覧ください.
フーリエ変換
定義
上記「指数関数型(複素形式)のフーリエ級数展開」と「フーリエ積分」を組み合わせると, 「指数関数型のフーリエ積分」が出来上がります.
$$ f(x) = \frac{1}{2 \pi} \int_{- \infty}^{\infty} \bigg[ \int_{- \infty}^{\infty} f( \xi ) \; e^{- i \omega \xi } \; d \xi \; \bigg] e^{i \omega x } d \omega $$
この中の
$$ \int_{- \infty}^{\infty} f( \xi ) \, e^{- i \omega \xi } \, d \xi $$
の部分を「フーリエ変換」と呼びます. これがフーリエ変換の定義です.
フーリエ変換
$$ \mathcal{F}[f] \, (\omega) = \int_{- \infty}^{\infty} f( \xi ) \; e^{- i \omega \xi } \; d \xi $$
フーリエ級数展開の係数に対応するのが, フーリエ積分におけるフーリエ変換の部分です. 両者を並べてじっくり眺めまわすとちょっと分かりやすくなります.
\begin{eqnarray} f(x) &=& \frac{1}{2 \pi} \int_{- \infty}^{\infty} \bigg[ \int_{- \infty}^{\infty} f( \xi ) \; e^{- i \omega \xi } \; d \xi \; \bigg] e^{i \omega x } d \omega \\ f(x) &=& \frac{1}{2 \pi} \sum_{m= – \infty}^{\infty} \bigg( \int_{- \pi}^{\pi} f(\xi ) e^{-im \xi } d \xi \bigg) e^{imx} \end{eqnarray}
詳しくは以下の記事をご参照ください.
フーリエ変換とは何か?指数関数型のフーリエ積分とフーリエ変換の定義
性質
フーリエ変換
$$ \mathcal{F}[f] \, (\omega) = \int_{- \infty}^{\infty} f( \xi ) \; e^{- i \omega \xi } \; d \xi $$
に対し, 以下に示す
$$ \mathcal{F}^{-1}[f] \, (x) = \frac{1}{2 \pi} \int_{- \infty}^{\infty} f( \xi ) \, e^{- i x \xi } \, d \xi $$
が, フーリエ逆変換です. 前に係数が付いていたり, 変数が入れ替わったりしています.
とある関数をフーリエ変換し, さらに逆フーリエ変換すると元の関数に戻ります. 便利な操作ですが, 本当にそうなるのかは以下の記事をご参照ください.
まとめ
以上, フーリエ変換についてでした.
本稿ではフーリエ変換の定義までを足早に解説したわけですが, 「フーリエ変換が何の役に立つのか」に関して一切触れませんでした.
実用上, フーリエ変換は「波の表示において, 時間と周波数を変換する道具」です. それが具体的に何を意味するのか, に関しましては, 実際にフーリエ変換が使われる場面で解説させていただきます.