当サイトは複素数がどのように応用されているのか?何の役に立つのか?に焦点を当て, 高校数学を修めた方向けにお話ししていきます.
日常生活で複素数に触れることは稀ですし, 頻繁に複素数を使った計算をする人はもっと稀です. 使わないと複素数の知識, 公式は頭の中からどんどん欠落していきます.
このページは複素数の基本を簡単に紹介し, 当サイト内のリンクをまとめます. 複素数の基本的な性質を忘れてしまったときに活用していただければ幸いです.
複素数, 虚数とは?
「2乗して負の値になる数」を『虚数』と呼びます. 「ルート(√ )の中が負になる数」と言い換えても良いでしょう.
虚数を用いることで数字の世界は実数世界から更に拡がります. 虚数を包含することで拡張された数が『複素数』です.
複素数が提唱されたのは16世紀ごろで, 負の値が認められたすぐ後です. 幾何学に比べれば大変新しい学問分野であると言えます.
複素数を考える上で, 『複素平面』(別名『ガウス平面』)という考え方は大変便利です. これまで実数という直線上にしかなかった数を, 複素数と言う平面上の数として考えます.
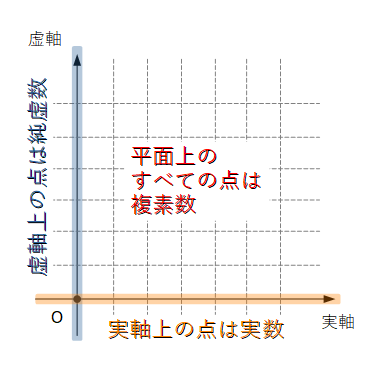
複素平面の何が便利かと言うと, 「平面上の座標の回転を簡単に表現できること」です. 複素数の極形式を使えば, 複素平面上の座標の回転は「複素数の掛け算」で表されます.
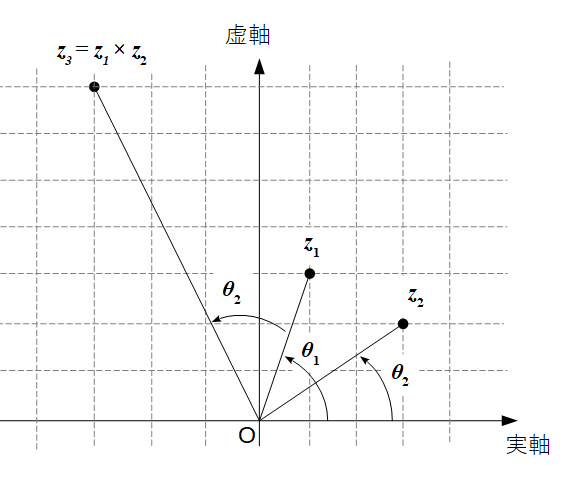
\( z_1 = r_1 (\cos{\theta _1} +i \sin{\theta _1} ) \) と \( z_2 = r_2 (\cos{\theta _2} +i \sin{\theta _2} ) \) という2つの複素数の掛け算を三角関数の加法定理を使って整理すると,
\begin{eqnarray} z_1 \times z_2 = r_1 r_2 \; \left( \, \cos{(\theta _1 + \theta _2)} + i \sin{(\theta _1 + \theta _2)} \, \right) \end{eqnarray}
となり, 座標上の点の回転と拡大を表していることが分かります.
オイラーの公式
オイラーの公式は複素数が他の学問分野に応用されるきっかけとなりました.
$$ e^{i \theta} = \cos{\theta} + i \sin{\theta} $$
この奇妙で美しい公式は, 導いたオイラー自身も意図しなかった効果を有し, 複素数に関する様々な問題を解決して, それらの関係性を明確にしました.
オイラーの公式は理解が難しい概念の1つ. オイラーの公式を理解する近道は指数関数と三角関数の定義に立ち返ることです.
複素指数関数の定義を考え、オイラーの公式を導出 (証明)する
オイラーの公式が「数学界の至宝」とまで称されるのは, この公式が, 複素数の実世界への応用に大きく貢献したからです.
波動を扱う多くの分野(量子力学, 電磁気, 結晶構造解析など)において, 波動の扱いを容易にし, フーリエ変換を導くことで, 信号解析の分野にも寄与しました.
まとめ
複素数の基礎を簡単にまとめました. 複素数の基本的な性質を忘れてしまったときに活用していただければ幸いです.