複素電力に複素共役が使われるのはなぜか？

今回のテーマは複素電力です. 複素電力は, 有効電力や無効電力, 位相差などを1つにまとめた便利な概念ですが, 定義や構造が分かりにくくなっています.

その定義を見たとき, 誰もが感じる疑問は「なぜ複素共役が用いられるのか？」ということでしょう. 本稿では, その疑問に応えていくことを目指します.

有効電力・無効電力

複素電力の話に入る前に関連する概念を抑えておきます.

交流回路にはコイルやキャパシタという要素が登場しますが, 理想的なコイルやキャパシタは電力を一時的に蓄積するだけで, 電力を消費する（熱や光に変換する）ことはありません. こうした特性から蓄積素子とも呼ばれます.

対して, 抵抗は電力を消費します.

ゆえに, 交流回路において電源が送り出す電力は, 「抵抗によって消費される電力」と「蓄積素子との間を行き来するだけで消費されない電力」に分けられます. 前者が「有効電力」の成分, 後者が「無効電力」の成分です.

蓄積素子が蓄積する電力と放出する電力の量は等しいため, 1周期の中で平均を取れば, 無効電力の成分は零になります.

数式で見る有効電力・無効電力

上で有効電力と無効電力の概念を大まかに説明しましたが, 次は「有効電力と無効電力の定義」を数式で見てみましょう.

交流回路における電圧, 電流を以下のように置きます.

\begin{eqnarray} v &=& \sqrt{2} V \sin{(\omega t- \phi)} \;\;\;\; \cdots \;\; (1) \\ i &=& \sqrt{2} I \sin{(\omega t- \phi -\theta)} \\ &=& \sqrt{2} I \left\{ \cos \theta \sin{(\omega t -\phi)} – \sin{\theta} \cos{(\omega t -\phi)} \right\} \;\;\; \cdots \;\; (2) \end{eqnarray}

ここで \(V\), \(I\) はそれぞれ電圧と電流の実効値, \(\omega\) は電源の角周波数, \(\phi\) は電圧の初期位相, \(\theta\) は電圧と電流の位相差を表します. 電流は加法定理で展開しました.

瞬時電力 \(p\) は電圧と電流の積であり, 以下のように表されます.

\begin{eqnarray} p=VI \cos\theta \left\{ 1-\cos{2(\omega t -\phi)} \right\} -VI \sin \theta \sin{2(\omega t -\phi)} \;\;\;\; \cdots \;\; (3) \end{eqnarray}

式中 \(\left\{ 1-\cos{2(\omega t -\phi)} \right\}\) の係数である \(VI \cos\theta\) が有効電力, \(\sin{2(\omega t -\phi)}\) の係数である \(VI \sin \theta\) が無効電力です.

有効電力・無効電力は, 「電力」と呼ばれますが, 実際には瞬時電力でも平均電力でもなく, 「瞬時電力の1成分の係数」です. ただし, 式(3) について1周期分の平均値を取ると, 有効電力と全く同じ値になるため, こちらを「有効電力」と呼ぶこともあります. この場合の有効電力は平均電力を意味します.

また, 電圧と電流それぞれの実効値を掛けた \(VI\) を皮相電力と呼びます.

有効電力, 無効電力については「有効電力と無効電力」で詳しく解説しました.

複素共役

続いて, 「複素共役」とは何だったか, について復習します.

複素共役とは, 「ある複素数の実部はそのままに, 虚部のみ \((-1)\) を掛けた複素数」のことです.

例えば, \(\dot{z}=\sqrt{3}+j\) という複素数の複素共役は \(\overline{\dot{z}}=\sqrt{3}-j\) になります.

極形式でも見てみましょう. 先ほどの \(z\) を極形式で表せば,

\begin{eqnarray} \dot{z}=2(\cos{\frac{\pi}{6}}+j\sin{\frac{\pi}{6}}) \;\;\;\; \cdots \;\; (4) \end{eqnarray}

ですが, この複素共役は,

\begin{eqnarray} \overline{\dot{z}} &=& 2(\cos{\frac{\pi}{6}}-j\sin{\frac{\pi}{6}}) \\ &=& 2(\cos \left( {-\frac{\pi}{6}} \right) +j\sin \left( {-\frac{\pi}{6}} \right) ) \;\;\;\; \cdots \;\; (5) \end{eqnarray}

となります. 即ち, 「複素共役を取る」という操作を極形式で見ると, 「位相に \((-1)\) を掛ける」という操作と同じものであると分かります.

「複素共役を掛ける」という操作

次に, 「複素共役を掛ける」とはどういうことなのか見ていきます.

大きさ \(1\) の2つの複素数 \(\dot{z}_1=\cos{\theta_1}+j\sin{\theta_1}\), \(\dot{z}_2=\cos{\theta_2}+j\sin{\theta_2}\) があったとき, この2数をそのまま掛けることを複素平面上で見ると下図のようになります.

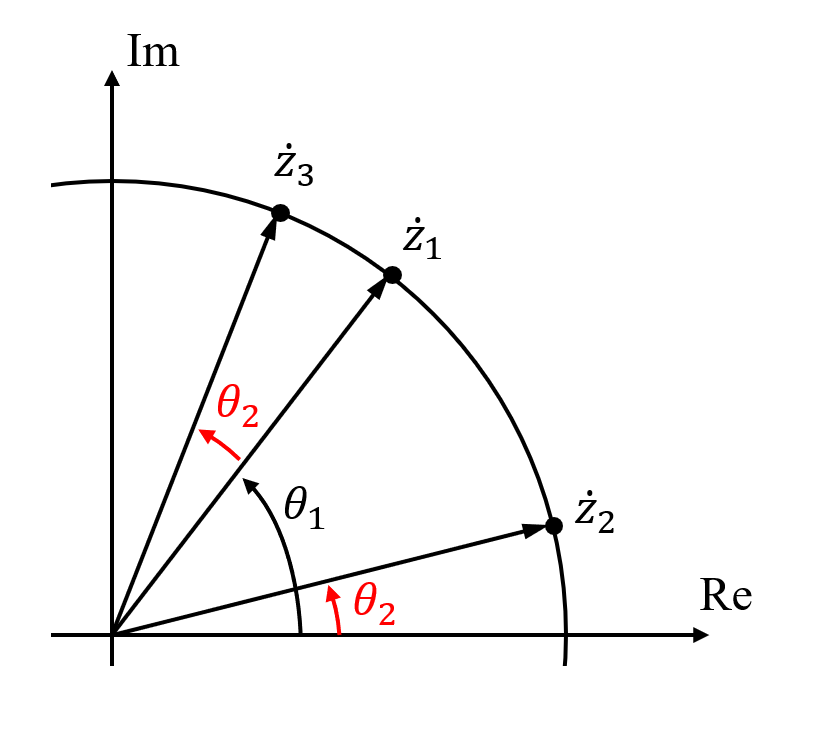
\(\dot{z}_1\) と \(\dot{z}_2\) の積である \(\dot{z}_3\) の位相は, \(\dot{z}_1\) と \(\dot{z}_2\) の位相の和になります.

対して, \(\dot{z}_2\) の複素共役である \(\overline{\dot{z}_2}\) を掛けると, 下図のようになります.

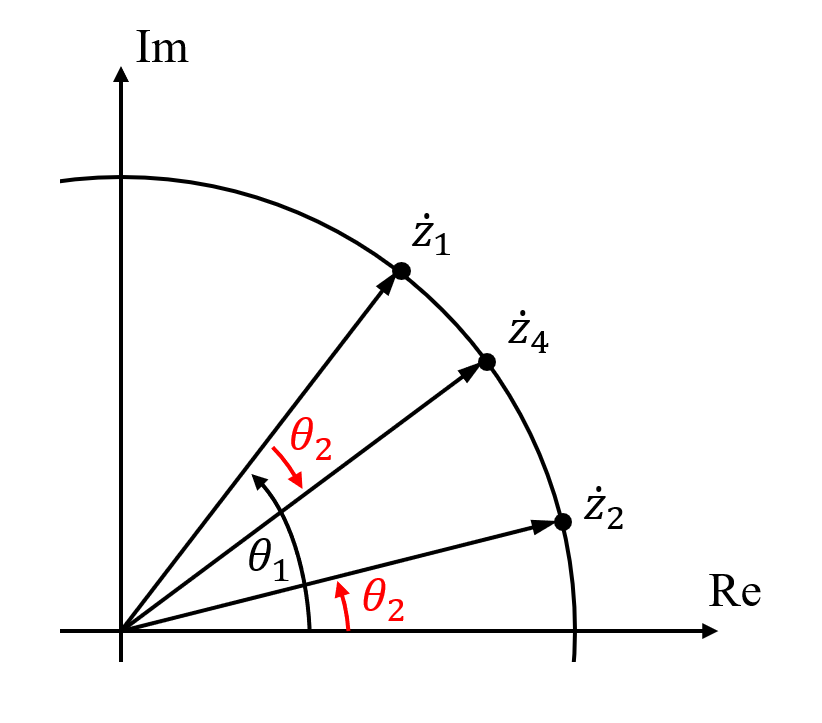
掛けてできた \(\dot{z}_4\) の位相は, \(\theta_1-\theta_2\) になっています. つまり, 「複素共役を掛ける」という操作を極座標で眺めれば, 「2数の位相差を取る」という操作であることが分かります.

また, ここでは大きさ \(1\) 同士の複素数を掛けたので大きさは変わりませんでしたが, 最終的にできる複素数の大きさは元の2数の大きさを掛けたものになります.

複素電力

ここから本題です. 複素電力の定義について触れていきます.

フェーザ表示した電圧及び電流を \(\dot{V}\), \(\dot{I}\) とすると, 複素電力 \(\dot{P}\) は以下で定義されます.

\begin{eqnarray} \dot{P}=\dot{V} \cdot \overline{\dot{I}} \;\;\;\; \cdots \;\; (6) \end{eqnarray}

複素電力とは「フェーザ表示した電圧に, フェーザ表示した電流の『複素共役』を掛けたもの」です.

複素電力の構造

複素電力の中身について, もう少し詳しく見ていきましょう.

電圧と電流をそれぞれフェーザ表示し,

\begin{eqnarray} \dot{V}= Ve^{j\theta_1} \;\;\;\; \cdots \;\; (7) \end{eqnarray}

\begin{eqnarray} \dot{I}= Ie^{j\theta_2} \;\;\;\; \cdots \;\; (8) \end{eqnarray}

と置くと, 複素電力は次のように表せます.

\begin{eqnarray} \dot{P}= VIe^{j(\theta_1 – \theta_2)} = VIe^{j\theta} &\;& \;\;\; \cdots \;\; (9) \\ \left( \theta=\theta_1 – \theta_2 \right) &\;& \end{eqnarray}

つまり, 複素電力とは, 「大きさが皮相電力, 位相が電圧-電流間の位相差である複素数」になっていることが分かります.

また, 指数関数部分をオイラーの公式で展開すると, 以下の形になります.

\begin{eqnarray} \dot{P}= VI \cos \theta + j VI \sin \theta \;\;\;\; \cdots \;\; (10) \end{eqnarray}

つまり, 実部は有効電力, 虚部は無効電力になっています.

\begin{eqnarray} \dot{P}= P_e +jP_r \;\;\;\; \cdots \;\; (11) \end{eqnarray}

式(11)を複素平面で表すと, こういうことです.

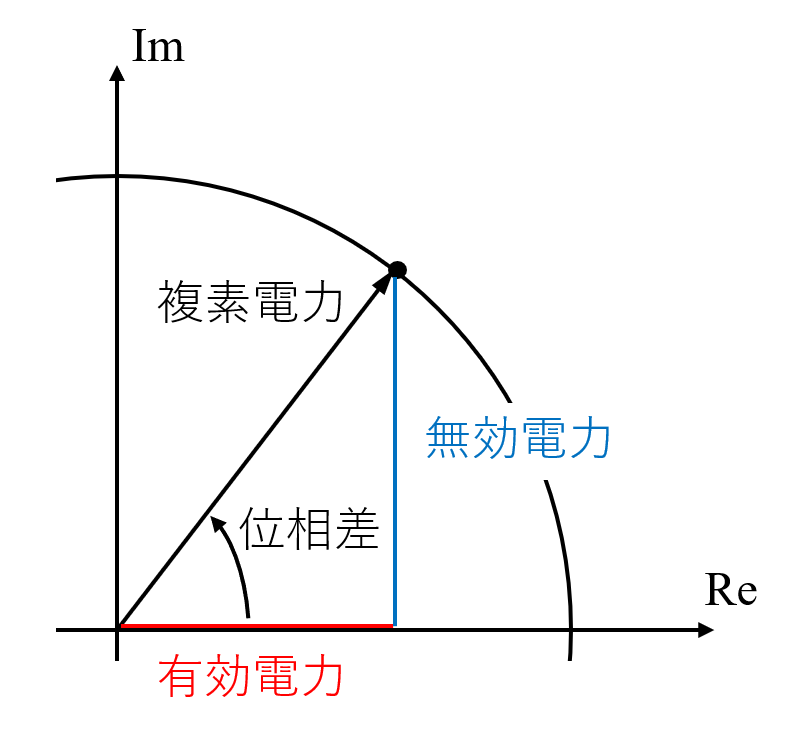
まとめると, 複素電力とは, 有効電力・無効電力・皮相電力・位相差などを複素平面上で一つに統合し, 扱いやすくした概念だと言えます.

様々な電力

中学からここまでに習ってきた『電力』をまとめて並べて見比べてみようと思います.

直流回路では, 電力・電圧・電流・抵抗の間に以下のような関係が成り立ちました.

\begin{eqnarray} P=V I=RI \cdot I = R I^2 \;\;\;\; \cdots \;\; (12) \end{eqnarray}

このような対応関係は交流回路においても各瞬時で成り立ちます.

\begin{eqnarray} p=v i=z_{ins} \cdot i \cdot i = z_{ins} \cdot i^2 \;\;\;\; \cdots \;\; (13) \end{eqnarray}

ただし, ここで出てくるインピーダンス \(z_{ins}\) は電圧や電流の位相情報をダイレクトに取り込んでいるため, 大変複雑で分かりにくい形をしています. 試しに, 式(1), (2) の形で表される電圧と電流からインピーダンスを計算すれば, 以下のようになります.

\begin{eqnarray} z_{ins} = \frac{V \sin{(\omega t- \phi)}}{I \sin{(\omega t- \phi -\theta)}} \;\;\;\; \cdots \;\; (14) \end{eqnarray}

この \(z_{ins}\) からは素子の情報を取り出すことができませんし, \(z_{ins}\) を用いた計算は大変面倒です.

一方, 交流回路をある程度長い時間で眺めたとき, 消費される電力（有効電力）は, 式(12), (13)と異なる形をしています.

\begin{eqnarray} P_e=VI \cos \theta \;\;\;\; \cdots \;\; (15) \end{eqnarray}

これは瞬時電力の中に含まれていた「無効電力」の成分がキャンセルされたためです.

最後に複素電力です.

\begin{eqnarray} \dot{P} = \dot{V} \overline{\dot{I}} = \dot{Z} \dot{I} \cdot \overline{\dot{I}} = \dot{Z} | \dot{I} |^2 \;\;\;\; \cdots \;\; (16) \end{eqnarray}

複素電力は直流電力や交流電力瞬時値が持っていた電圧・電流などとの対応関係を保持しています. また, 複素インピーダンスは大変扱いやすいシンプルな構造を持っているため, 電力に関する計算を簡単にしてくれます.

なぜ複素共役を掛けるのか？

ここまでの内容をまとめると, 複素電力には以下のような性質があります.

・直流回路と同じような, 電力・電圧・電流・インピーダンスの対応関係を持ち, 計算が簡単.

・有効電力と無効電力両方の情報を持ち, 両者の大きさが一目で分かる.

複素電力の定義の中に複素共役が登場する理由を端的に述べるならば, 上記のような性質を複素電力に持たせたかったからだと言えます. 複素共役ではない電流と電圧を掛け合わせただけでは, 上記2つの性質は得られません.

有効電力（\(P_e=VI \cos \theta\)）, 無効電力（\(P_r=VI \sin \theta\)）のどちらの定義にも位相差（\(\theta\)）が登場しますが, 「複素共役を掛ける」という操作は, この「位相差」を取り出すために用いられました. 複素共役を掛けることで意味のある物理量を導出しているのです.

まとめ

ご覧いただきありがとうございました.

本稿は, 以前に執筆した複素電力に関する記事における私の誤りをとある先生にご指摘いただき, 再度執筆したものです. ご指摘いただけたこと, この場を借りて御礼申し上げます.