閉路方程式の対称性と相反定理

前回に引き続き, 閉路電流や閉路方程式に関する記事です.

今回は, 閉路方程式が持つ対称性を紹介しつつ, この対称性を使って相反定理（可逆定理）を証明していきます.

復習：閉路電流法

まずは閉路電流法の復習から始めていきましょう.

閉路電流法とは, 枝電流を閉路電流で置き換えることで回路を流れる電流を算出する解析方法でした.

手順は以下の通りです.

1. 閉路を還流する電流を仮定する.
2. キルヒホッフの電圧則から閉路方程式を導出する.
3. 解く.

ここでは （閉路1周における電圧降下の合計）=（閉路1周における起電力の合計）という形になる式を閉路方程式と呼んでいます.

閉路電流法の厳密な説明には線形代数の知識が必要になるため, 高校までの物理ではふわっとした議論しかなされていませんでした. 閉路電流を行列で定義し, 補枝電流との関係を明らかにすると, 閉路電流と補枝電流は全く同じものを表していることが分かります. このあたりのことは前回記事で説明しました.

「閉路電流法と補木枝電流」

例題：キャンベルブリッジ

復習も兼ねて, 閉路電流法の例題を解いてみます. 図1をご覧ください.

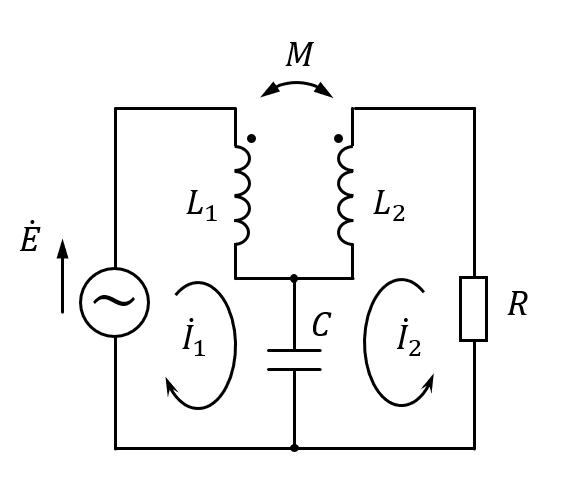
図1に示しますのは, キャンベルブリッジと呼ばれる周波数測定回路です.

「ブリッジ」と呼ばれる回路は中学や高校でも幾つか登場しました. ブリッジ回路には様々な種類があります.

ホイートストンブリッジは抵抗を計測するための回路で, 測定器に流れる電流を零にすることで測定器の内部抵抗を無視し, 精度良く抵抗値を算出できるという回路でした.

同様にマクスウェルブリッジという回路もあります. こちらは未知のインダクタンスを測定するための回路です.

そして, 図1のキャンベルブリッジは入力された交流電圧の周波数を測定するための回路です. 相互インダクタンスの大きさを可変にし, 抵抗（計測器）に流れる電流を零にすることで, そのときの周波数を正確に算出できます.

キャンベルブリッジの閉路方程式

それでは, 図1のキャンベルブリッジにおいて抵抗 R に流れる電流が零になるように調整し, そのときの相互インダクタンス \(M\) と 容量 \(C\) の値から, 電源周波数を算出してみましょう.

閉路電流 \(\dot{I}_2=0\) を解いて, そのときの \(\omega\) を求めます.

まずは, 図1 で設定した閉路電流に沿って, 閉路方程式を立てます.

\begin{eqnarray} \begin{array} \; \left( j\omega L_1+\frac{1}{j\omega C} \right) \dot{I}_1+\left( j\omega M+\frac{1}{j\omega C} \right) \dot{I}_2=\dot{E} \\ \; \left( j\omega M+\frac{1}{j\omega C} \right) \dot{I}_1+\left( j\omega L_2+R+\frac{1}{j\omega C} \right) \dot{I}_2=0 \end{array} \;\;\; \cdots (1) \end{eqnarray}

この閉路方程式を行列表示すれば以下のようになります.

\begin{eqnarray} \left[ \begin{array}{cc} j\omega L_1+\frac{1}{j\omega C} & j\omega M+\frac{1}{j\omega C} \\ j\omega M+\frac{1}{j\omega C} & j\omega L_2+R+\frac{1}{j\omega C} \end{array} \right] \left[ \begin{array}{rr} \dot{I}_1 \\ \dot{I}_2 \end{array} \right]=\left[ \begin{array}{rr} \dot{E} \\ 0 \end{array} \right] \;\;\; \cdots (2) \end{eqnarray}

\(\dot{I}_1\), \(\dot{I}_2\) は一般に零でないので, この係数行列は逆行列を持つはずです. ここで, 係数行列を \(A\) とすると, \(\dot{I}_2\) は以下のように表せます.

\begin{eqnarray} \dot{I}_2=|A|^{-1} \left( j \omega M+\frac{1}{j \omega C} \right) \dot{E} \;\;\; \cdots (3) \end{eqnarray}

\(|A|\) と \(\dot{E}\) は零ではないので, \(\dot{I}_2=0\) となる条件は,

\begin{eqnarray} j \omega M+1/(j \omega C)=0 \;\;\; \cdots (4) \end{eqnarray}

\(\omega\) について解けば, このときの周波数は, \(\omega=1/\sqrt{MC}\) であることが分かりました.

上記のように, 閉路方程式を導出し係数行列の逆行列を左から作用させれば, 閉路電流を機械的に求めることができます.

閉路方程式における係数行列の対称性

式(2)の行列表示した閉路方程式を見ると係数行列 \(A\) が対称（対角行列）になっていますが, これは偶然ではありません.

式(2)は \(2\times2\) の係数行列を持つ閉路方程式ですが, \(3\times3\)以上の閉路方程式（つまり, 独立な閉路が3つ以上存在する回路における閉路方程式）においても, 係数行列は一般に対称です. これを示していきましょう.

電源 \(\dot{E}_k\), 抵抗 \(R_k\), インダクタ \(L_k\), キャパシタ \(C_k\) を含む枝k を仮定します. このとき, この枝の両端の電圧 \(\dot{V}_k\) と枝電流 \(\dot{I}_k\) の関係は以下のように表されます.

\begin{eqnarray} \dot{V}_k=\dot{E}_k+\left( R_k+j\omega L_k+\frac{1}{j\omega C_k} \right) \dot{I}_k \;\;\; \cdots (5) \end{eqnarray}

ここで, 後の議論のために, 複素ベクトルを以下のように定義しておきます.

\begin{eqnarray} \dot{{\boldsymbol V}}=\left[ \begin{array}{cc} \; \dot{V}_1 \\ \vdots \\ \dot{V}_b \end{array} \right] , \; \dot{{\boldsymbol E}}=\left[ \begin{array}{cc} \; \dot{E}_1 \\ \vdots \\ \dot{E}_b \end{array} \right] , \; \dot{{\boldsymbol I}}=\left[ \begin{array}{cc} \; \dot{I}_1 \\ \vdots \\ \dot{I}_b \end{array} \right] , \; \dot{{\boldsymbol I}}_{loop}=\left[ \begin{array}{cc} \; \dot{I}^1 \\ \vdots \\ \dot{I}^b \end{array} \right] \end{eqnarray}

ここで, 下付き数字が付与された電流（\(\dot{I}_k\)）は枝電流, 上付き数字が付与された電流（\(\dot{I}^k\)）は閉路電流を表します.

このように定義すると, 回路全体の電流-電圧特性を以下のように表すことができます.

\begin{eqnarray} \dot{{\boldsymbol V}}= \dot{{\boldsymbol E}}-Z_x \dot{{\boldsymbol I}} \;\;\; \cdots (6) \end{eqnarray}

ここで, \(Z_x\) は対角行列であり, 中身は以下のようになっています.

\begin{eqnarray} Z_x &=& \left[ \begin{array}{rrr} \dot{z}_{11} & \; & 0 \\ \; & \ddots & \; \\ 0 & \; & \dot{z}_{bb} \end{array} \right] , \\ \; \\ \; &{ \rm{\;} }& \; \dot{z}_{kk}=R_{kk}+j\omega L_{kk}+\frac{1}{j\omega C_{kk} } \;\; ( 1 \leq k \leq b, k \in \mathbb{Z} ) \end{eqnarray}

また, 前回扱った「枝電流と閉路電流の関係」, 及びキルヒホッフの電圧則より,

\begin{eqnarray} \dot{{\boldsymbol I}}=B^T \dot{{\boldsymbol I}}_{loop} \;\;\; \cdots (7) \end{eqnarray}

\begin{eqnarray} B \dot{{\boldsymbol V}}={\boldsymbol 0} \;\;\; \cdots (8) \end{eqnarray}

であり, この関係式を用いて式(6)を変形すると, 以下のように閉路方程式が導出されます.

\begin{eqnarray} \dot{{\boldsymbol V}} &=& \dot{{\boldsymbol E}}-Z_x B^T \dot{{\boldsymbol I}}_{loop} \\ B \dot{{\boldsymbol V}} &=& B \dot{{\boldsymbol E}}-BZ_x B^T \dot{{\boldsymbol I}}_{loop} \\ BZ_x B^T \dot{{\boldsymbol I}}_{loop} &=& B \dot{{\boldsymbol E}} \;\;\; \cdots (9) \end{eqnarray}

ここで, \((B Z_x B^T)^T=B Z_x B^T \) であることから, 閉路方程式の係数行列は対称性を持つことが示されました.

ここまでは相互誘導がない場合を考えましたが, 相互誘導がある場合にも対称になっていることが確認できます.

例えば, 枝1と枝2のインダクタ間に相互誘導を考えると, \(Z_x\) には,

\begin{eqnarray} Z_x =\left[ \begin{array}{rrrrr} j\omega L_1 & j\omega M & \; & \; 0 \\ j\omega M & j\omega L_2 & \; & \; & \; \\ \; & \; & \dot{z}_{33} & \; & \; \\ \; & \; & \; & \ddots & \; \\ 0 & \; & \; & \; & \dot{z}_{bb} \end{array} \right] \;\;\; \cdots (10) \end{eqnarray}

のように, 対称に誘導成分が表れます. どのように枝を選んでも相互誘導の成分が対称に表れることは変わりなく, 係数行列は必ず対称です.

また, 上記から係数行列の対角成分には相互誘導以外のインピーダンスが表れ, 相互誘導の効果は対角成分以外の場所に表れることが分かります.

相反定理

閉路方程式の係数行列が対称であれば, 閉路方程式を立てるときに間違いに気付きやすくなります. しかし, それだけではありません.

可逆定理とも呼ばれる「相反定理」は閉路方程式の係数行列が対称であることを利用して導出することが可能です. ちょっとやってみましょう.

\(m\)個の電圧源を持つ回路

電圧源 \(\dot{E}_1\), \(\cdots\), \(\dot{E}_m\) を含む回路で閉路方程式を立てることを考えます. 1つの枝に複数の電圧源が存在する場合は合成して 1つの電圧源と考えることができるため, 1つの枝に含まれる電圧源の数は 1つ以下としておきましょう.

今回は, 電圧源 \(\dot{E}_k\) に流れる電流を閉路電流 \(\dot{I}_k\) として選びます. 「補木枝の数 \(\leq\) 電圧源の数」であればこれで閉路方程式が完成しますが, 一般には方程式の数が足りていません. 1次独立な解を算出するためには, この他の独立な閉路が必要です.

そこで, 電源を含まず, 既に選ばれている閉路とは独立な閉路の閉路電流 \(\dot{I}_{m+1}\), \(\cdots\), \(\dot{I}_l\) を補い, 閉路方程式を立てることとします.

\(m\) は電圧源の数, \(l\) は補木枝の数です. このように閉路電流を選べば, 閉路方程式は以下のように表されます.

\begin{eqnarray} \left[ \begin{array}{rr} z_{11} & z_{12} \\ z_{21} & z_{22} \end{array} \right] \; \left[ \begin{array}{r} \dot{{\boldsymbol I}}_1 \\ \dot{{\boldsymbol I}}_2 \end{array} \right]=\left[ \begin{array}{c} \dot{{\boldsymbol E}}_1 \\ \dot{{\boldsymbol 0}} \end{array} \right] \;\;\; \cdots (11) \end{eqnarray}

ここで, \(z_{11}\), \(z_{12}\), \(z_{21}\), \(z_{22}\) は係数行列の部分行列で, それぞれ \(m\times m\), \(m\times (l-m)\), \((l-m)\times m\), \((l-m)\times (l-m)\) の大きさを持っています. \(\dot{{\boldsymbol I}}_1\), \(\dot{{\boldsymbol I}}_2\), \(\dot{{\boldsymbol E}}_1\), \(\dot{{\boldsymbol 0}}\) はそれぞれベクトルであることにご注意ください.

式(11)から, \(\dot{{\boldsymbol I}}_2\) を消去すると,

\begin{eqnarray} \dot{{\boldsymbol E}}_1 = \left( z_{11}-z_{12}{z_{22}}^{-1} z_{21} \right) \dot{{\boldsymbol I}}_1 \;\;\; \cdots (12) \end{eqnarray}

となります. \( \dot{{\boldsymbol E}}_1 \) と \( \dot{{\boldsymbol I}}_1 \) を関係付ける行列を \(Z\) とし,

\begin{eqnarray} Z = z_{11}-z_{12}{z_{22}}^{-1} z_{21} \;\;\; \cdots (13) \end{eqnarray}

とすれば, 「閉路方程式の対称性」から, \(z_{11}\) と \(z_{22}\) は対角行列で, \({z_{12}}^T=z_{21}\) なので, \(Z\) も対称であることが分かります.

m端子対回路

状況を整理してみましょう.

今, \(m\)個の電圧源を持つ回路において, それぞれの電圧源を流れる電流 \( \dot{{\boldsymbol I}}_1\) と 電圧 \( \dot{{\boldsymbol E}}_1 \) の関係が, 行列 \(Z\) を用いて, 式(12) 及び 式(13) のように表されることが分かりました. 電圧源を外部に引き出した図3 のような回路を考えるとイメージしやすいですが, これはまさしく, 「m端子対回路」を表しています.

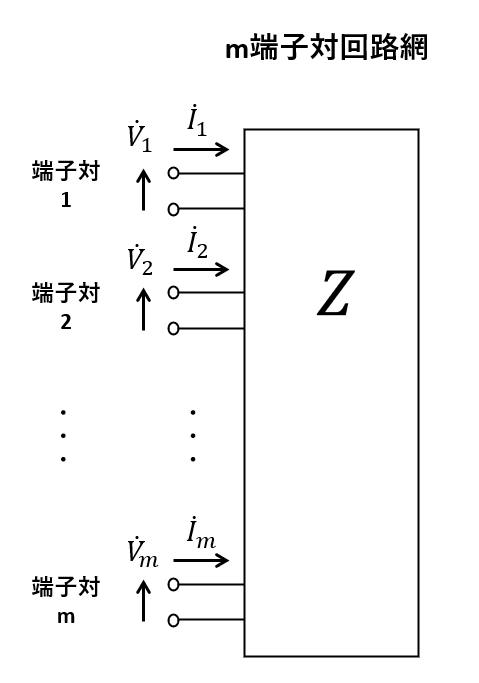
ここで登場した \(Z\) とは, \(m\)個存在する端子対における電圧と電流を関係付ける行列であり, それは要するに「インピーダンス行列」です. つまり, m端子対回路のインピーダンス行列は対称性を持つことが分かりました.

さらに, 「対角行列の逆行列も対角行列である」ので, インピーダンス行列の逆行列であるアドミタンス行列も対称性を持ちます.

m端子対回路やインピーダンス行列については, 以下のリンクをご参照ください.

「n端子対回路網の行列表現とZ行列・F行列・S行列の相互変換」

2端子対回路における相反定理

ここまでは m端子対回路について考えてきましたが, ここからは 2端子対回路に話を絞ります. 下図のような 2端子対回路において, 各端子対における電流と電圧の関係を表してみましょう.

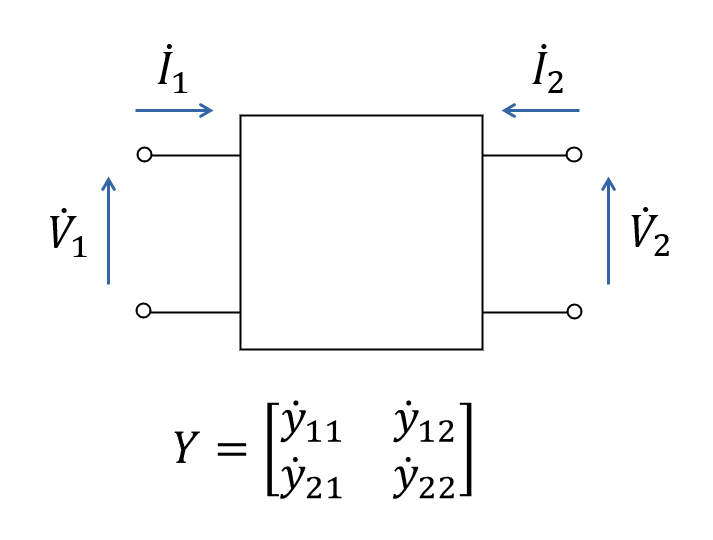
\begin{eqnarray} \left[ \begin{array}{cc} \; \dot{I}_1 \\ \; \dot{I}_2 \end{array} \right]=\left[ \begin{array}{cc} \; \dot{y}_{11} & \dot{y}_{12} \\ \; \dot{y}_{21} & \dot{y}_{22} \end{array} \right] \; \left[ \begin{array}{cc} \; \dot{V}_1 \\ \; \dot{V}_2 \end{array} \right] \;\;\; \cdots (14) \end{eqnarray}

式(14) では, 式(11) の場合と異なり, \(\dot{I}_1\), \(\dot{I}_2\), \(\dot{V}_1\), \(\dot{V}_2\) はベクトルではないことにご注意下さい.

この回路のポート2 を短絡（\(\dot{V}_2=0\)）して, ポート1 に電圧源 \(\dot{E}_R\) を接続すると, 式(14)より, ポート2 を流れる電流は,

\begin{eqnarray} \dot{I}_2=\dot{y}_{21} \dot{E}_R \;\;\; \cdots (15) \end{eqnarray}

となります. 同様に, ポート1 を短絡（\(\dot{V}_1=0\)）して, ポート2 に電圧源 \(\dot{E}_R\) を接続すると, ポート1 を流れる電流は, 以下のようになります.

\begin{eqnarray} \dot{I}_1=\dot{y}_{12} \dot{E}_R \;\;\; \cdots (16) \end{eqnarray}

先ほど示した「m端子対回路のアドミタンス行列は対称性を持つ」ということから, \(\dot{y}_{12}=\dot{y}_{21}\) なので, このとき, 式(15) におけるポート2 と式(16) におけるポート1 には同じ大きさの電流が流れていることが分かります. よって, 次のことが言えます.

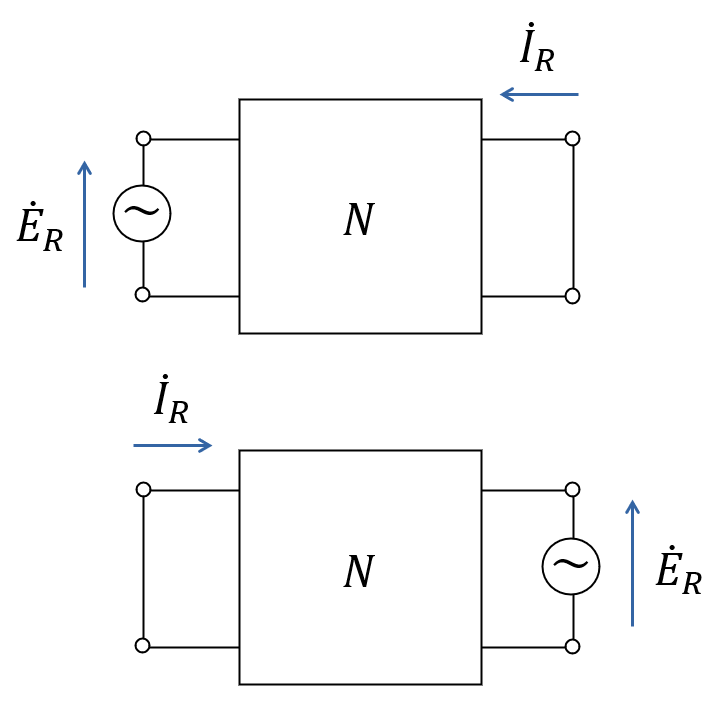
「2端子対回路において『電圧源の位置』と『電流』を交換することができる」.

これが相反定理です.

文章だと分かりにくいですが, 図にすると少し分かりやすくなります. 下図は相反定理を表した図です. この \(N\) が 2端子対回路網であれば, 上の回路と下の回路のような電圧源位置の交換が実行できます.

様々な相反定理の表現

相反定理には様々な表現があります.

式(14)の 2端子対回路において,

・ポート2 を短絡させ, ポート1 に電圧源 \(\dot{E}_{a}\) を接続したとき, ポート2 に流れる電流を \(\dot{I}_{a}\)
・ポート1 を短絡させ, ポート2 に電圧源 \(\dot{E}_{b}\) を接続したとき, ポート1 に流れる電流を \(\dot{I}_{b}\)

とすれば, \(\dot{y}_{12}=\dot{y}_{21}\) より, 以下の関係が導かれます.

\begin{eqnarray} \frac{\dot{E}_a}{\dot{I}_a}=\frac{\dot{E}_b}{\dot{I}_b} \;\;\; \cdots (17) \end{eqnarray}

これもまた相反定理です. こちらの表現の方が広い範囲をカバーしています.

どちらの表現においても, その元となっているのは「\(\dot{y}_{12}=\dot{y}_{21}\)」. つまり, 「インピーダンス（アドミタンス）行列が対称性を持つ」という事実です.

\(\dot{A}\dot{D}-\dot{B}\dot{C}=1\)

インピーダンス行列の対称性は, F行列の持つ有益な性質を導出します.

F行列もインピーダンス行列と同じく 2端子対回路における電圧と電流を関係付ける行列です. 詳しくは「2端子対回路網概説」をご参照ください.

F行列 \(F=\left[ \begin{array}{rr} \dot{A} & \dot{B} \\ \dot{C} & \dot{D} \end{array} \right]\) は上述の 2端子対回路における電流, 電圧と以下の関係を持ちます.

\begin{eqnarray} \; \left[ \begin{array}{cc} \; \dot{V}_1 \\ \; \dot{I}_1 \end{array} \right]=\left[ \begin{array}{cc} \; \dot{A} \; & \dot{B} \\ \; \dot{C} \; & \dot{D} \end{array} \right] \left[ \begin{array}{cc} \; \dot{V}_2 \\ \; \dot{I}_2 \end{array} \right] \;\;\; \cdots (18) \end{eqnarray}

また, インピーダンス行列とは次の関係によって, 相互に変換することが可能です.

\begin{eqnarray} \, \dot{A} &=& \frac{ \dot{z}_{11} }{ \dot{z}_{21} } \\ \, \\ \, \dot{B} &=& \frac{ \dot{z}_{11} \dot{z}_{22} – \dot{z}_{12} \dot{z}_{21} }{ \dot{z}_{21} } = \frac{ |Z| }{ \dot{z}_{21} } \\ \, \\ \, \dot{C} &=& \frac{ 1 }{ \dot{z}_{21} } \\ \, \\ \, \dot{D} &=& \frac{ \dot{z}_{22} }{ \dot{z}_{21} } \end{eqnarray}

インピーダンス行列の成分を使って \(|F|=\dot{A}\dot{D}-\dot{B}\dot{C}\) を計算すると,

\begin{eqnarray} \; |F| = \frac{\dot{z}_{11}}{\dot{z}_{21}} \cdot \frac{\dot{z}_{22}}{\dot{z}_{21}}-\frac{\dot{z}_{11}\dot{z}_{22}-\dot{z}_{12}\dot{z}_{21}}{\dot{z}_{21}} \cdot \frac{1}{\dot{z}_{21}} = \frac{\dot{z}_{12}\dot{z}_{21}}{{\dot{z}_{21}}^2} = \frac{\dot{z}_{12}}{\dot{z}_{21}} \end{eqnarray}

となりますが, インピーダンス行列の対称性から \(\dot{z}_{12}=\dot{z}_{21}\) なので, \(|F|=1\) となります.

これを使えば, 式(18) の左側から F行列の逆行列を掛けることで, 入力端と出力端を容易に交換することができます.

\begin{eqnarray} \left[ \begin{array} \; \dot{V}_2 \\ \; \dot{I}_2 \end{array} \right]=\left[ \begin{array}{cc} \; \dot{D} & -\dot{B} \\ \; -\dot{C} & \dot{A} \end{array} \right] \left[ \begin{array} \; \dot{V}_1 \\ \; \dot{I}_1 \end{array} \right] \;\;\; \cdots (19) \end{eqnarray}

F行列のこうした性質も「インピーダンス行列の対称性」から導かれています.

まとめ

最後までご覧いただきありがとうございます.

今回の内容をまとめますと, 以下のようになります.

(i). 閉路方程式の係数行列は対称性を持つ
(ii). (i)から, m端子対回路におけるインピーダンス行列の対称性が導かれる
(iii). (ii)から, 2端子対回路における相反定理が導かれる

今回は 2端子対回路における相反定理を扱いましたが, 次回はこれをさらに拡張してテレゲンの相反定理を紹介します. どうぞよろしくお願いします.