2端子対回路概説

回路の解析や設計において, 2端子対回路（4端子回路）は大変便利な概念です.

本稿は「2端子対回路網, 回路網行列とは何か？」, 「\(F\)行列, \(Z\)行列, \(Y\)行列の相互変換」, 「回路の接続」など, 2端子対回路に関する内容を網羅的に概説します.

2端子対回路網とは

端子とは回路の中のある 1点を指し, 端子対とは「端子 2つを合わせて 1組にしたもの」を表します.

端子対には条件があり, 端子対を構成する 2つの端子において, 片方の端子に電流が入り込むのなら, もう片方の端子からは同じ大きさの電流が出て行かなければなりません.

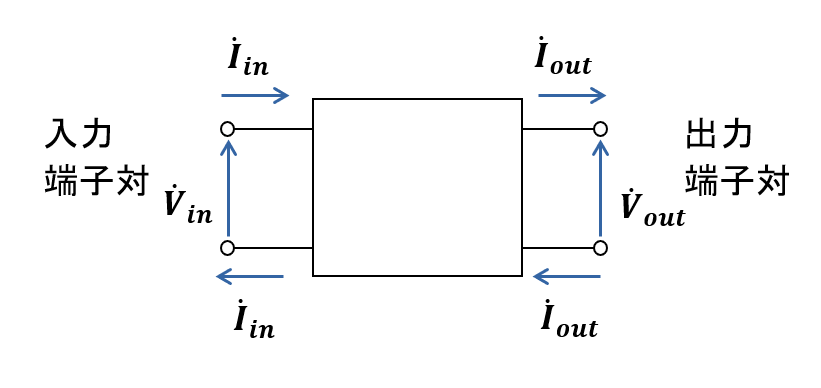
例えば, 電源の入力端子と出力端子は端子対になっています. 他にもコンセントに挿すプラグの 2つの突起は端子対です.

この端子対 2つで囲まれた, 端子を 4つ持つ回路網を「2端子対回路網」と呼びます. コンセントと電化製品を繋ぐ「電源ケーブル」は, 両端が端子対なので, 2端子対回路網と言えます.

2端子対回路網は, 私たちが普段目にする電化製品の中に多数存在するため, 2端子対回路網の単位で回路を切り分けると, 回路の解析や設計が簡単になります.

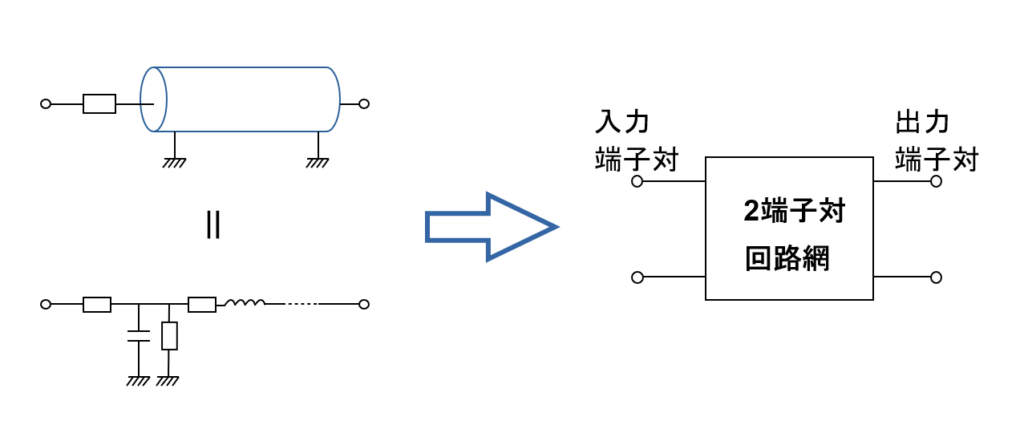
2端子対回路網を描くときは一般に, 左側に入力端子対, 右側に出力端子対を取ります. 回路網の構成要素が線形素子（電流が電圧に比例する回路部品. キャパシタやコイルや純抵抗）だけならば入力端子対と出力端子対は入れ替えても問題ありません. 見る方向が逆になるだけです.

非線形素子（ダイオードやトランジスタや電源）が含まれるときには入力と出力を勝手に入れ替えることはできません.

2端子対回路網は 4つの端子で構成される回路網であるため, 「4端子回路網」と呼ぶこともあります. 英語で端子対は「ポート（port）」なので, 「2ポート回路網」と呼ばれることもありますが, 同じものです.

4端子行列（\(F\)行列）

2端子対回路という考え方は, 中学 1年生で習う「関数」と同じように考えるとイメージしやすいでしょう.

関数（函数）とは, 「とある入力に依存した出力をする箱」です. 例えば, 1次関数は \( x \) という入力に対して \( y=ax + b \) という出力を返します.

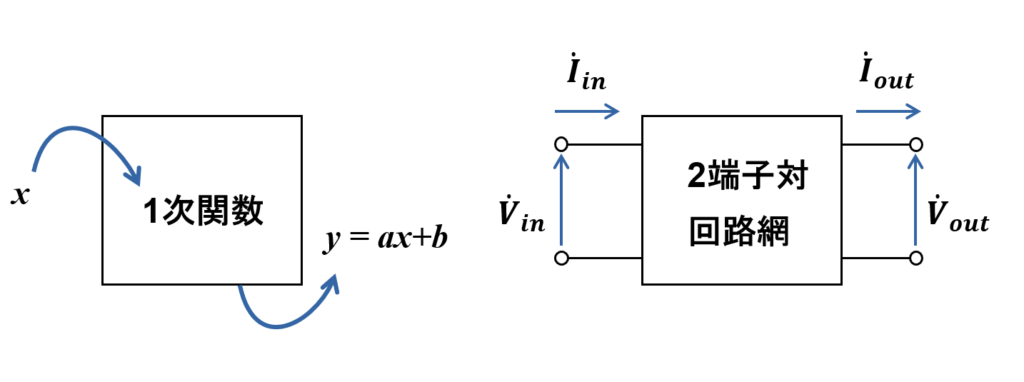
2端子対回路には 2つの入力と, 2つの出力があります. 入力電圧 \( \dot{V_{in}} \) , 入力電流 \( \dot{I_{in}} \) , 出力電圧 \( \dot{V}_{out} \) , 出力電流 \( \dot{I}_{out} \) （電流も電圧もフェーザ表示）です.

回路が現実に存在し, 入力電圧と入力電流が決まっているなら, 出力電圧と出力電流は当然 1つの値に決まります. 逆もまた然り. 出力の 2つが決まっていれば, 入力の 2つも決まるはずです.

回路が線形素子のみで構成されているとき, 入力と出力の関係は, 4つの複素数 \( \dot{A} \) , \( \dot{B} \) , \( \dot{C} \) , \( \dot{D} \) を使って以下のように表せることが知られています.

\begin{eqnarray} \left\{ \begin{array} \, \dot{V}_{in} = \dot{A} \, \dot{V}_{out} + \dot{B} \, \dot{I}_{out} \; \cdots \; (1) \\ \, \dot{I}_{in} = \dot{C} \, \dot{V}_{out} + \dot{D} \, \dot{I}_{out} \; \cdots \; (2) \end{array} \right. \end{eqnarray}

4元1次の連立方程式が出来ました. 係数 \( \dot{A} \) , \( \dot{B} \) , \( \dot{C} \) , \( \dot{D} \) 及び, 変数 \( \dot{V}_{in} \) , \( \dot{I}_{in} \) , \( \dot{V}_{out} \) , \( \dot{I}_{out} \) の8つの内どれか6つが分かれば, 残りの2つを自動的に求められる連立方程式です.

この連立方程式は行列の形で表すこともできます.

\begin{eqnarray} \left[ \begin{array} \, \dot{V}_{in} \\ \, \dot{I}_{in} \end{array} \right] = \left[ \begin{array}{rr} \dot{A} & \dot{B} \\ \dot{C} & \dot{D} \end{array} \right] \, \left[ \begin{array} \, \dot{V}_{out} \\ \, \dot{I}_{out} \end{array} \right] \end{eqnarray}

上記の手順で導かれる, 回路に固有の（入出力電圧, 電流の大きさや周波数に依存しない）行列 \begin{eqnarray} F= \left[ \begin{array}{rr} \dot{A} & \dot{B} \\ \dot{C} & \dot{D} \end{array} \right] \end{eqnarray} を「4端子行列」, または「\(F\)行列」と呼びます.

この \( F \) は Four-terminal の \( F \) だと言う人もいれば, Fondamental（基本的な）の \( F \) だと言う人もいます.

\(F\)行列を求める

回路網を構成する素子が線形素子のみの場合, \(F\)行列は入出力の電圧や電流の大きさ, 及び周波数に依存しない, という特徴があります. よって, \(F\)行列が既知であれば, 「入力から出力」, 「出力から入力」が簡単に計算できて便利です.

そして, 入出力に依存しないという性質を用いることで \(F\)行列は簡単に求められます.

\(F\)行列の求め方

ここからは \(F\)行列の求め方を解説していきます.

まず, 出力端子対を開放（則ち, 出力端子に無限大の大きさの抵抗を挿入）して入力端子対に一定の交流電圧を印加し, 出力端子対に掛かる電圧を測定します.

出力端子対が開放されているので, 出力端子対に電流は流れず（\( \dot{I}_{out} = 0 \)）, 式(1) はこうなります.

$$ \, \dot{V}_{in} = \dot{A} \, \dot{V}_{out} \; \cdots \; (1)^{\prime} $$

式(1)\(^{\prime} \) において入力電圧を出力電圧で割れば \(\dot{A}\) を求めることが可能です.

次は \(\dot{B}\) を求めるため, 出力端子対を短絡（出力端子を導線で接続）して, 入力端子対に掛かる電圧と出力端子対に流れる電流を測定します.

出力端子対が短絡されているので, 出力端子対には電位差が存在せず（\( \dot{V}_{out} = 0\)）, 式(1) はこう.

$$ \, \dot{V}_{in} = \dot{B} \, \dot{I}_{out} \; \cdots \; (1)^{\prime \prime} $$

式(1)\(^{\prime \prime}\) の入力電圧を出力電流で割れば \(\dot{B}\) が求められます.

\(\dot{A}\) は電圧を電圧で割って求められる無次元の物理量ですが, \(\dot{B}\) は電圧を電流で割って求めるので単位は \([\mathrm{ \Omega }]\) です. \(\dot{A}\) , \(\dot{B}\) は同じ行列の中にある要素ですが, 単位がそれぞれ異なることにご注意下さい.

上記のような導出方法に由来して, \(\dot{A}\) , \(\dot{B}\) にはそれぞれ 「開放電圧比」, 「短絡伝達インピーダンス」という名前が付けられています.

残りの \(\dot{C}\) , \(\dot{D}\) についても出力端子対を開放したり短絡したりしつつ, 電圧や電流を測定して 式(2) を使うことで求められます. \(\dot{C}\) は開放伝達アドミタンス（単位 \([\mathrm{ S }]\)）, \(D\) は短絡電流比（無次元）という名前です.

求めるときに入力端子の方を開放したり短絡したりできるのならばそうやって求めても問題ありません. 入力端子対と出力端子対は本質的に等価であり, 交換可能です. ただし, 線形素子で構成される回路に限ります.

補足： \(F\)行列の威力

\( F \)行列を求めるプロセスで大事なのは「回路の中身に一切触れていない」ということです.

回路の一部（もしくは全部）をブラックボックス化するこの考え方を使えば, 回路の中身を考えずとも回路の電気的な応答を把握できます.

この考え方は様々な電気測定で応用されます.

ミクロな世界で電子がどういうパスを通って, どこに行く, 何が起こる, ということに対して, マクロな世界に生きる私たちは想像することしかできません. しかし, 試料内部がどのような構造であっても, （内部で線形な応答のみが起こっていると仮定すれば）コイルとキャパシタと抵抗で構成される一意な回路へと置き換えることができます.

コイル, キャパシタ, 抵抗に対応する物理現象を考察することで間接的に物質の内部構造を知ることができるのです.

様々な回路網行列

2端子対回路網を記述する行列は 1種類ではありません. 他にも, 状況によって便利な行列が幾つかあります. 以下では, そのうちの 2つを紹介します.

インピーダンス行列（\(Z\)行列）

左辺に入力電圧と出力電圧, 右辺に入力電流と出力電流を持ってくると, 以下のような行列の式ができます.

\begin{eqnarray} \left[ \begin{array} \, \dot{V}_{in} \\ \, \dot{V}_{out} \end{array} \right] = \left[ \begin{array}{rr} \dot{Z}_{11} & \dot{Z}_{12} \\ \dot{Z}_{21} & \dot{Z}_{22} \end{array} \right] \, \left[ \begin{array} \, \dot{I}_{in} \\ \, \dot{I}_{out} \end{array} \right] \end{eqnarray}

この \(Z = \left[ \begin{array}{rr} \dot{Z}_{11} & \dot{Z}_{12} \\ \dot{Z}_{21} & \dot{Z}_{22} \end{array} \right]\) をインピーダンス行列（\(Z\)行列）と呼びます. \(Z\)行列の要素はすべて単位が \( [\mathrm{ \Omega }] \) です.

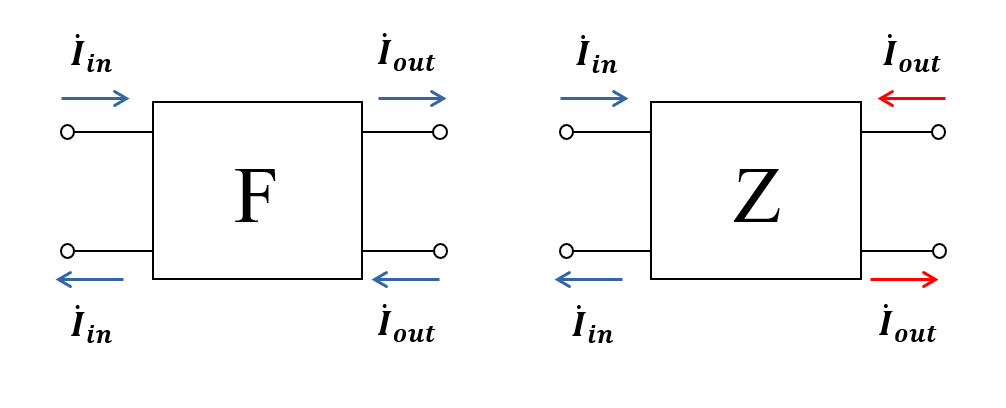
ここで注意なのですが, \(F\)行列を考えるときの出力電流 \( \dot{I}_{out} \) と, \(Z\)行列を考えるときの出力電流 \( \dot{I}_{out} \) は, 向きを逆にして定義しています. これは, 後述する「回路の接続」において, こちらの方が便利だからです.

アドミタンス行列（\(Y\)行列）

同じように, 左辺に入力電流と出力電流, 右辺に入力電圧と出力電圧を持ってくると, 行列要素の単位がすべて [ \( \mathrm{S} \)（ジーメンス）] になるアドミタンス行列（\(Y\)行列）ができます.

\begin{eqnarray} \left[ \begin{array} \, \dot{I}_{in} \\ \, \dot{I}_{out} \end{array} \right] = \left[ \begin{array}{rr} \dot{Y}_{11} & \dot{Y}_{12} \\ \dot{Y}_{21} & \dot{Y}_{22} \end{array} \right] \, \left[ \begin{array} \, \dot{V}_{in} \\ \, \dot{V}_{out} \end{array} \right] \end{eqnarray}

アドミタンス行列を考えるときの電流の向きはインピーダンス行列のときと同じにしています.

各行列の関係と相互変換

名前からも分かる通り, \(Y\)行列とは \(Z\)行列の逆行列のことで, \(Z\)行列と \(Y\)行列は相互に変換可能です.

$$ Y= Z^{-1} = \frac{1}{|Z|} \cdot \left[ \begin{array}{rr} \dot{Z}_{22} & – \dot{Z}_{12} \\ – \dot{Z}_{21} & \dot{Z}_{11} \end{array} \right] $$

\(Z\)行列と \(F\)行列も書き方が違うだけ. 本質的に表しているものは同じなので相互に変換できます.

\(Z\)行列を用いた電流電圧の関係式と, \(F\)行列を用いた式では, 出力電流 \( \dot{I}_{out} \) の向きが異なることに注意しましょう. \(F\)行列を使ったときの電流の向きを正とすると, 以下の式が立てられます.

\begin{eqnarray} \left[ \begin{array} \, \dot{V}_{in} \\ \, \dot{V}_{out} \end{array} \right] = \left[ \begin{array}{rr} \dot{Z}_{11} & \dot{Z}_{12} \\ \dot{Z}_{21} & \dot{Z}_{22} \end{array} \right] \, \left[ \begin{array} \, \dot{I}_{in} \\ \, – \dot{I}_{out} \end{array} \right] \end{eqnarray}

連立方程式の形にすれば,

\begin{eqnarray} \left\{ \begin{array} \, \dot{V}_{in} = Z_{11} \dot{I}_{in} – Z_{12} \dot{I}_{out} \; \cdots \; (3) \\ \, \dot{V}_{out} = Z_{21} \dot{I}_{in} – Z_{22} \dot{I}_{out} \; \cdots \; (4) \end{array} \right. \end{eqnarray}

(1) ~ (4)式を使って \(F\)行列の要素を求めると,

\begin{eqnarray} \, \dot{A} &=& \left( \frac{ \dot{V}_{in} }{ \dot{V}_{out} } \right) _{\dot{I}_{out = 0} } = \frac{ \dot{Z}_{11} }{ \dot{Z}_{21} } \\ \, \dot{B} &=& \left( \frac{ \dot{V}_{in} }{ \dot{I}_{out} } \right) _{\dot{V}_{out = 0} } = \frac{ \dot{Z}_{11} \dot{Z}_{22} – \dot{Z}_{12} \dot{Z}_{21} }{ \dot{Z}_{21} } = \frac{ |Z| }{ \dot{Z}_{21} } \\ \, \dot{C} &=& \left( \frac{ \dot{I}_{in} }{ \dot{V}_{out} } \right) _{\dot{I}_{out = 0} } = \frac{ 1 }{ \dot{Z}_{21} } \\ \, \dot{D} &=& \left( \frac{ \dot{I}_{in} }{ \dot{I}_{out} } \right) _{\dot{V}_{out = 0} } = \frac{ \dot{Z}_{22} }{ \dot{Z}_{21} } \end{eqnarray}

となります.

電流の向きの取り方で符号が反転し, 参考書によっては上記と異なる符号となる場合もありますので, 十分注意してください.

本質的に, \(F, Z, Y\)行列は同じもの（2端子対回路の応答）を表しているため, 相互変換できます. では, なぜ幾つも種類があるかと言うと, それぞれ得意なことが異なるためです.

\(F\)行列は縦続接続, \(Z\)行列は直列接続, \(Y\)行列は並列接続をするとき, 有効に機能します.

2端子対回路網の接続

回路網行列を使うと, 2端子対回路網同士を接続することができます.

\(F\)行列による縦続接続

\(F\)行列を使うことで可能となるのが「縦続接続」です. 下図をご覧ください.

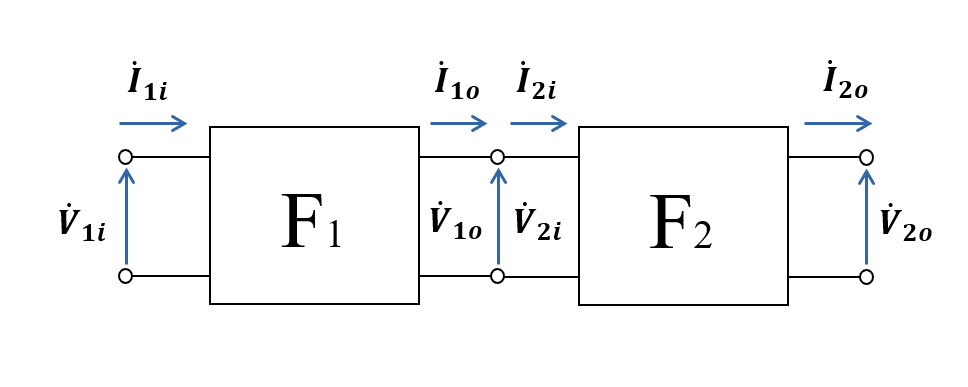
縦続接続とは 2端子対回路網の出力端子対と別の回路網の入力端子対を接続することです.

図中左側の回路網の \(F\)行列を \(F_1 = \left[ \begin{array}{rr} \dot{A}_1 & \dot{B}_1 \\ \dot{C}_1 & \dot{D}_1 \end{array} \right] \), 右側の回路網の \(F\)行列を \(F_2 = \left[ \begin{array}{rr} \dot{A}_2 & \dot{B}_2 \\ \dot{C}_2 & \dot{D}_2 \end{array} \right] \) と置くと, 電流電圧の関係は以下のように表されます.

\begin{eqnarray} \left[ \begin{array} \, \dot{V}_{1i} \\ \, \dot{I}_{1i} \end{array} \right] &=& \left[ \begin{array}{rr} \dot{A}_1 & \dot{B}_1 \\ \dot{C}_1 & \dot{D}_1 \end{array} \right] \, \left[ \begin{array} \, \dot{V}_{1o} \\ \, \dot{I}_{1o} \end{array} \right] \; \cdots \; (5) \\ \rm{ } \\ \left[ \begin{array} \, \dot{V}_{2i} \\ \, \dot{I}_{2i} \end{array} \right] &=& \left[ \begin{array}{rr} \dot{A}_2 & \dot{B}_2 \\ \dot{C}_2 & \dot{D}_2 \end{array} \right] \, \left[ \begin{array} \, \dot{V}_{2o} \\ \, \dot{I}_{2o} \end{array} \right] \; \cdots \; (6) \end{eqnarray}

左側回路網の出力端子対と右側回路網の入力端子対は一致しているので, 電流と電圧についての以下の関係が成り立ちます.

\begin{eqnarray} \left[ \begin{array} \, \dot{V}_{1o} \\ \, \dot{I}_{1o} \end{array} \right] = \left[ \begin{array} \, \dot{V}_{2i} \\ \, \dot{I}_{2i} \end{array} \right] \; \cdots \; (7) \end{eqnarray}

式(5) ~ (7)より, 以下の式が導かれます.

\begin{eqnarray} \left[ \begin{array} \, \dot{V}_{1i} \\ \, \dot{I}_{1i} \end{array} \right] &=& \left[ \begin{array}{rr} \dot{A}_1 & \dot{B}_1 \\ \dot{C}_1 & \dot{D}_1 \end{array} \right] \, \left[ \begin{array}{rr} \dot{A}_2 & \dot{B}_2 \\ \dot{C}_2 & \dot{D}_2 \end{array} \right] \, \left[ \begin{array} \, \dot{V}_{2o} \\ \, \dot{I}_{2o} \end{array} \right] \; \cdots \; (8) \end{eqnarray}

式(8) の意味するところは, 「縦続接続（出力端子対と入力端子対の接続）は \(F\)行列の積で表される」ということです. これは回路を 3つ, 4つと縦続に接続する場合にも適用できます.

\(Z\)行列による直列接続

下図のように 2端子対回路網を接続することを直列接続と呼びます.

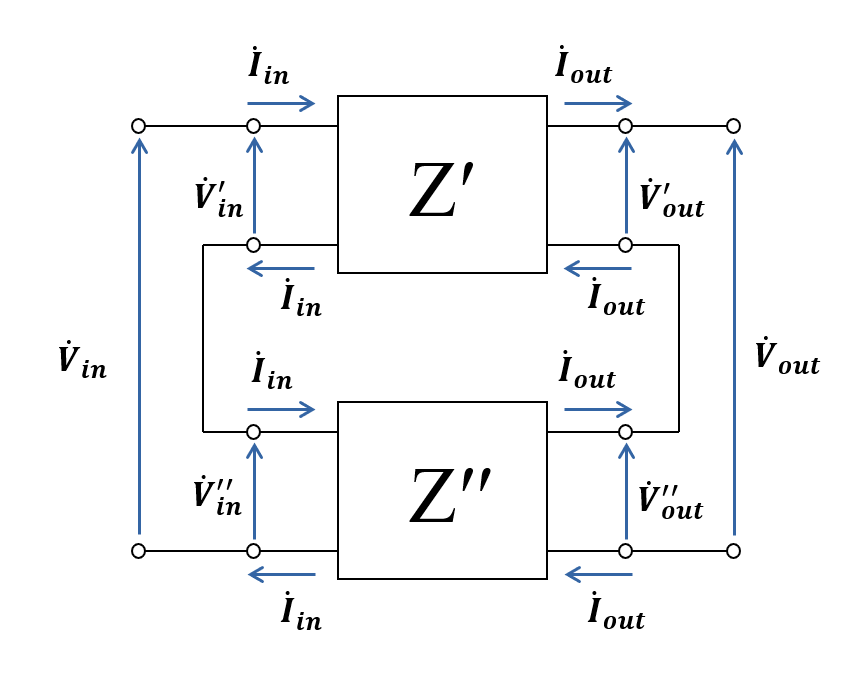
図中右側の端子をすべて消去すれば, 中学までに習った直列接続と同じ形であり, 1端子対回路網における直列接続を拡張した概念であることが分かります.

図中の電圧は以下の関係にあります.

\begin{eqnarray} \left[ \begin{array} \, \dot{V}_{in} \\ \, \dot{V}_{out} \end{array} \right] = \left[ \begin{array} \, \dot{V}_{in}^{\prime} \\ \, \dot{V}_{out}^{\prime} \end{array} \right] \, + \, \left[ \begin{array} \, \dot{V}_{in}^{\prime \prime} \\ \, \dot{V}_{out}^{\prime \prime} \end{array} \right] \; \cdots \; (9) \end{eqnarray}

\(Z\)行列を用いて (9)式を整理すると,

\begin{eqnarray} \left[ \begin{array} \, \dot{V}_{in} \\ \, \dot{V}_{out} \end{array} \right] = Z^{\prime} \, \left[ \begin{array} \, \dot{I}_{in} \\ \, \dot{I}_{out} \end{array} \right] \, + \, Z^{\prime \prime} \, \left[ \begin{array} \, \dot{I}_{in} \\ \, \dot{I}_{out} \end{array} \right] = \left\{ Z^{\prime} \, + \, Z^{\prime \prime} \right\} \, \left[ \begin{array} \, \dot{I}_{in} \\ \, \dot{I}_{out} \end{array} \right] \; \cdots \; (10) \end{eqnarray}

となり, 「2端子対回路網の直列接続は \(Z\)行列の和で表される」ことが分かります.

ここで注意すべきことは, 電流の関係です. 回路の接続前には入力端子対に入る電流と出ていく電流は大きさが同じでしたが, この関係は回路の接続後も保たれていなければなりません. 回路の接続によって入出力電流の関係が崩れる場合は, \(Z\)行列による直列接続の計算はできません.

\(Y\)行列による並列接続

「回路の直列接続が得意なのが \(Z\)行列」ならば, 「並列接続が得意なのが \(Y\)行列」です.

「2端子対回路網の並列接続」とは以下のような接続を指します.

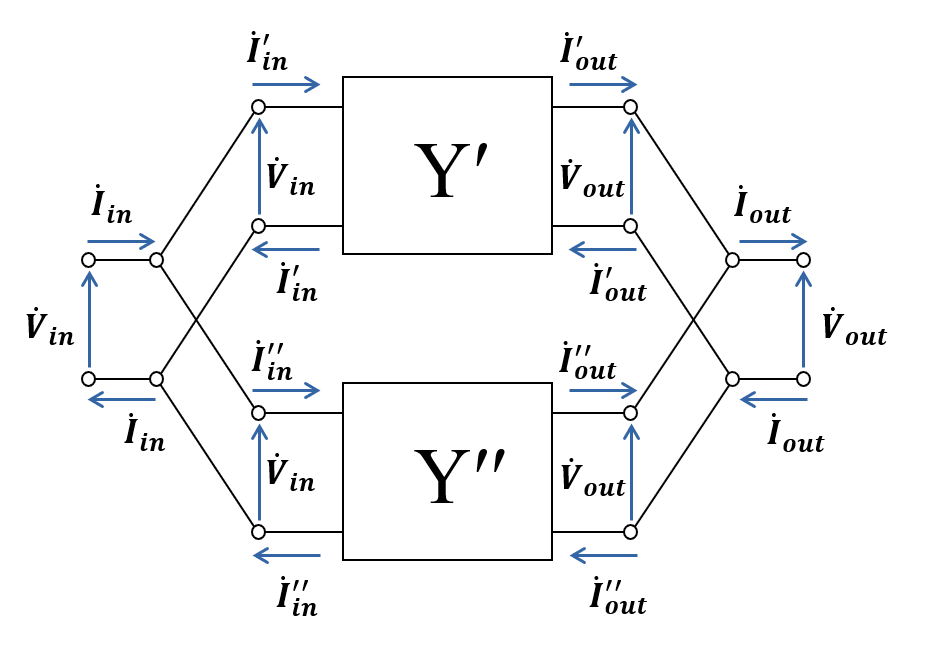
図中電流は以下の関係にあります.

\begin{eqnarray} \left[ \begin{array} \, \dot{I}_{in} \\ \, \dot{I}_{out} \end{array} \right] = \left[ \begin{array} \, \dot{I}_{in}^{\prime} \\ \, \dot{I}_{out}^{\prime} \end{array} \right] \, + \, \left[ \begin{array} \, \dot{I}_{in}^{\prime \prime} \\ \, \dot{I}_{out}^{\prime \prime} \end{array} \right] \; \cdots \; (11) \end{eqnarray}

\(Y\)行列を用いて整理すると,

\begin{eqnarray} \left[ \begin{array} \, \dot{I}_{in} \\ \, \dot{I}_{out} \end{array} \right] = Y^{\prime} \, \left[ \begin{array} \, \dot{V}_{in} \\ \, \dot{V}_{out} \end{array} \right] \, + \, Y^{\prime \prime} \, \left[ \begin{array} \, \dot{V}_{in} \\ \, \dot{V}_{out} \end{array} \right] = \left\{ Y^{\prime} \, + \, Y^{\prime \prime} \right\} \, \left[ \begin{array} \, \dot{V}_{in} \\ \, \dot{V}_{out} \end{array} \right] \; \cdots \; (12) \end{eqnarray}

となります. (11)式は「2端子対回路網の並列接続は \(Y\)行列の和で表される」ことを意味します. \(Y\)行列の並列接続においても \(Z\)行列のときと同じく, 「入出力電流の関係が保たれていること」に注意が必要です.

まとめ

本稿の内容を簡単にまとめます.

1. 2端子対回路網とは, 2つの端子対で囲まれた回路網のこと.
2. 2端子対回路網が線形素子のみで構成されている場合, 回路網をブラックボックスとして, 入出力のみから回路の特性を決めることができる.
3. 2端子対回路の応答を表す各種行列（回路網行列）は, 相互に変換できる.
4. \(F\)行列は縦続接続, \(Z\)行列は直列接続, \(Y\)行列は並列接続を容易にする.