分布定数回路と電信方程式
高校までに習った回路の知識では『電線』を取り扱うことができません. これは, 電線の回路要素が薄く広く分布しているためです.
架空線や海底ケーブルなどを扱うためには「分布定数回路」を用います. 本稿では, 新しく出てきた「分布定数回路」という概念, また, 電信方程式について解説します.
今回の話を理解するためには「極限」と「微分方程式」についての知識が必要です. 分からなくなったらその辺りのことを復習してみてください.
目次
分布定数回路とは
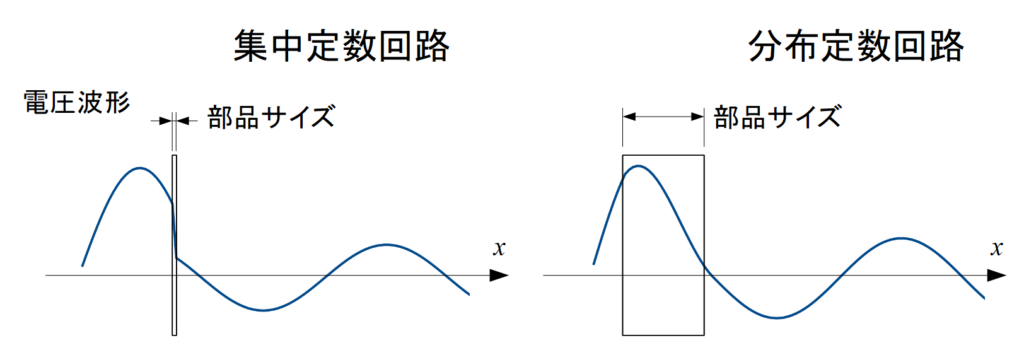
高校までに習ってきた全ての回路は, 入力する交流電圧の波長よりも十分小さなサイズの電子部品で構成されていました.
電圧・電流分布は各部品の中で均一であるとみなすことができ, 部品のサイズは無視できます. このように「電圧・電流の波長 \( \gg \) 部品のサイズ」となる回路を集中定数回路と呼びます.
一方, 架空線(いわゆる『電線』)や海底ケーブルなど, 電圧・電流の波長と同程度のサイズの回路要素を扱う場合, 内部の電圧・電流分布はケーブル全体に渡って均一であるとみなすことができません. ケーブル内部で場所によって電圧・電流の位相が異なるのです.
また, 波長と部品サイズの関係は相対的なものです. 高周波信号を扱う場合には信号の波長がとても短くなるため, 電子部品が小さくても内部の電圧・電流の位相が一様と見なせなくなります.
このように「電圧・電流の波長 \( \approx \) 部品のサイズ」となる回路を分布定数回路と呼びます.
分布定数回路には, 集中定数回路とは異なる扱いが必要です.
LCRで構成される分布定数回路
分布定数回路を数式で取り扱う方法について例を挙げつつ解説していきます.
ここでは, 抵抗 \( r \), インダクタ \( \ell \), キャパシタ \( c \), コンダクタ \( g \)(それぞれ単位長さ当たり) で構成される分布定数回路の例として, 同軸ケーブルについて考えていきましょう.
同軸ケーブルとは電気通信に使われるケーブルです. 断面を見ると, 内側から順に「内部導体」→「絶縁体」→「外部導体」→「保護被覆」が同心円上に配置された構造になっています. 内部導体を覆う外部導体が電磁シールドの役割を果たすため, 外部からの電磁波の影響を受けにくいことが特徴です.
ご家庭ではテレビコンセントとテレビを繋ぐケーブルに用いられます.

A : 保護被覆, B : 外部導体, C : 絶縁体, D : 内部導体(wikipedia 「同軸ケーブル」より)
同軸ケーブルの等価回路は以下のように表されます.
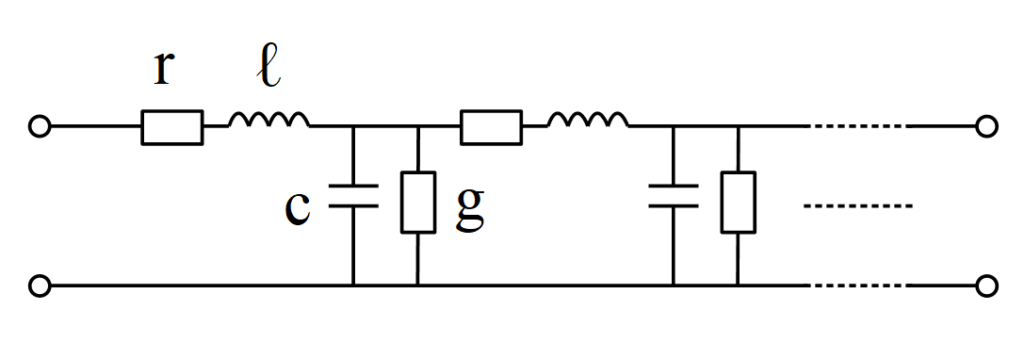
ここで, \( r \), \( \ell \), \( c \), \( g \) は単位長さ当たりの値であり, 上記回路は無限個の要素で構成される「分布定数回路」です.
上記等価回路において \( r \) と \( \ell \) が上の導線には存在して, 下の導線には存在しないことに疑問を持つ方もいらっしゃるかもしれません.
これは等価回路を簡略化したためです. 内部導体と外部導体の材質はほぼ同じなので, 本来は上の導線と同じ抵抗, インダクタが下の導線にも存在します. しかし, 適切に \( r \), \( \ell \) を配置すれば「上下の導線に抵抗とインダクタを分けた場合」も「片方の導線にまとめて描いた場合」も導出される式が同じになります. であれば等価回路図は可能な限りシンプルな方が好ましく, 片方の導線にまとめて描いた, という次第です.
目的と方針
同軸ケーブルの等価回路である上記分布定数回路を数学で扱って参ります.
今回知りたいのは, 「分布定数回路にインプットを与えると, どのようなアウトプットが得られるのか」ということです. 例えば, 集中定数回路要素である純抵抗を流れる電流は \( I=V/R \) のように, 印加電圧と抵抗の値で表すことができます. このように, 分布定数回路における電圧・電流を数式で表したいのです.
この関係を表した式が「電信方程式」で, とりあえずの目標は, この電信方程式を導出することになります.
具体的には, 「入力端子対に電圧 \( \dot{V}_1 \), 電流 \( \dot{I}_1 \) を加えたとき, 入力端子対から距離 \( x \) の位置における電圧 \( \dot{V} (x) \), 電流 \( \dot{I} (x) \) がどのように表されるか」を調べていきます.
無限分割
電信方程式を導出する方法は様々です.
例えば, 「集中定数回路からスタートし, 分割する回数を増やしていく」という方法があります.
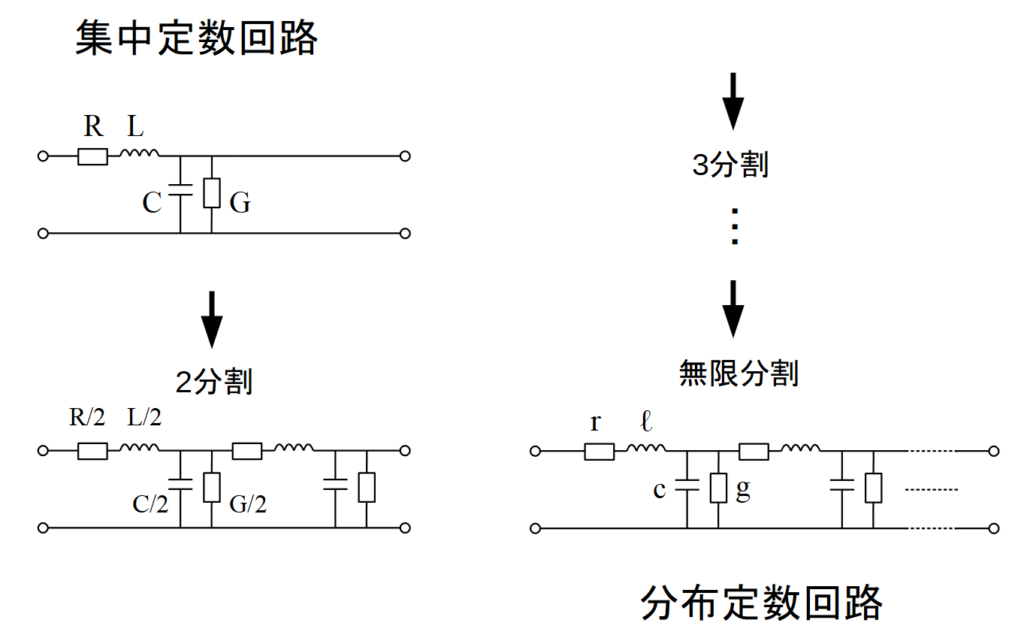
\( R \), \( L \), \( C \), \( G \) で構成される集中定数回路であれば, 入出力電圧, 電流の関係を表すことは難しくありません. これを次々に分割していきます. 2分割, 3分割, \( \cdots \) と繰り返していき, 無限回分割すれば分布定数回路になります. つまり, \(n\)分割したときの電圧・電流を数列で導出し, その数列の極限を考えるわけです.
上記方法でも良いのですが, 今回は簡単のため, 「微小区間」を考え, 「電圧と電流についての連立偏微分方程式を立てて解く」という方針で参ります.
微小区間で方程式を立てる
上記 \( r \), \( \ell \), \( c \), \( g \) から成る分布定数回路において, 時刻 \( t \), 入力端から距離 \( x \) の位置における微小区間 \( \Delta x \) に注目します.
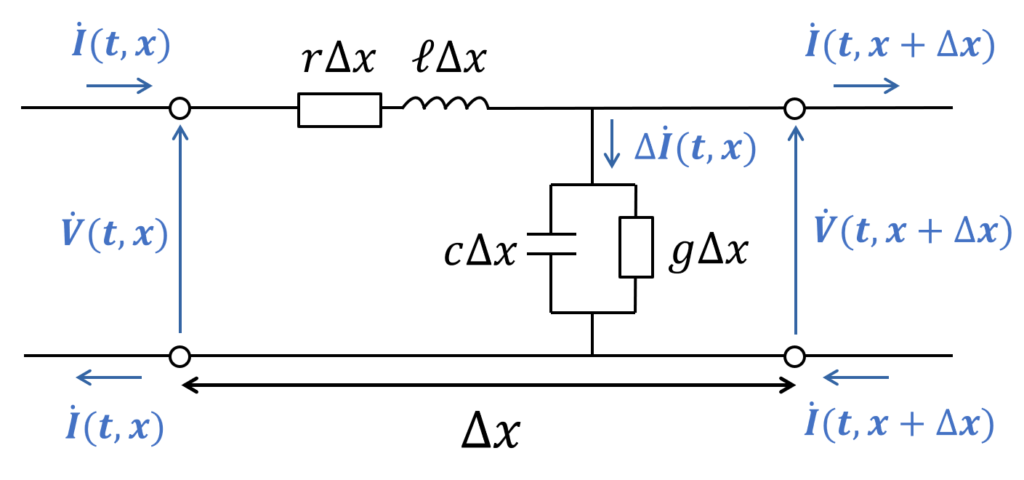
図中の電流, 電圧はすべてフェーザ表示です.
ここで重要なことは「微小区間である」ということです. 微小区間 \( \Delta x \) においては回路要素は波長に比べて十分小さいので, 集中定数とみなすことができます. つまり, 通常の抵抗やキャパシタのように扱うことが可能です.
微小区間 \( \Delta x \) 内に均一に分布している各成分は, 微小区間内のとある 1点に集中し, \( r \, \Delta x \), \( \ell \, \Delta x \), \( c \, \Delta x \), \( g \, \Delta x \) と表せると仮定して考えを進めることができます.
抵抗とインダクタンスの合成インピーダンス \( \dot{z} \Delta x \) は,
$$ \dot{z} \Delta x = (r + j \omega \ell ) \cdot \Delta x $$
キャパシタとコンダクタンスの合成アドミタンス \( \dot{y} \, \Delta x \) は,
$$ \dot{y} \Delta x = (g + j \omega c) \cdot \Delta x $$
ここで, \( \omega \) は角周波数を表します.
キャパシタのアドミタンスが \( j \omega c \cdot \Delta x \) になる理由が良く分からない方は以下の記事をご参照ください.
合成インピーダンスと合成アドミタンスを使うことで, 上記微小区間の回路をより簡略化したものが下の図6です.
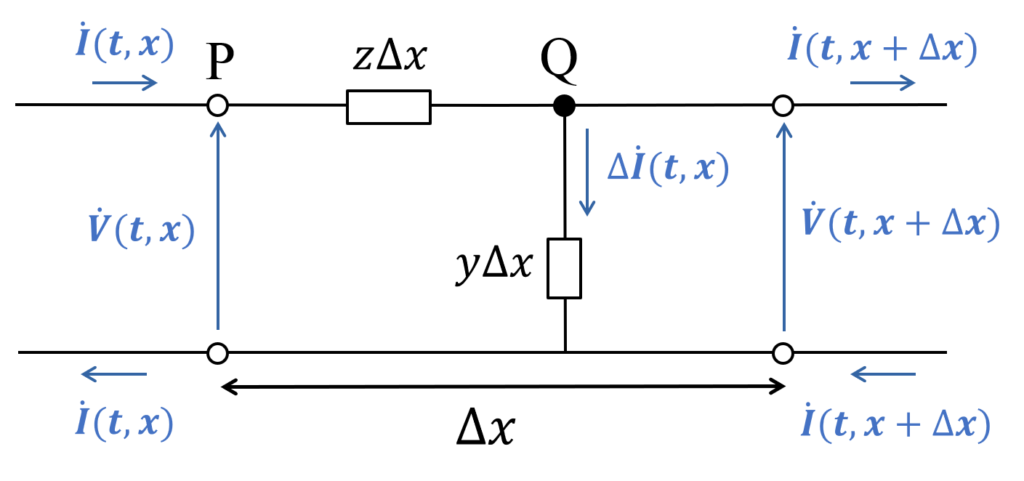
簡略化した分布定数回路を使って電流と電圧の関係式を導出します.
まず, 図中の節点Qに流れ込む(流れ出る)電流の関係に注目すると, 以下の式が立てられます.
\begin{eqnarray} – \Delta \dot{I} (t, x) &=& \dot{I} (t, x) \, – \, \dot{I} (t, x + \Delta x) \\ \rm{ } \\ &=& \dot{y} \Delta x \, \cdot \, \dot{V} (t, x) \; \cdots \; (1) \end{eqnarray}
次に, 図中 PQ間の電圧降下(電位の変化量)を考えると, 以下の式が導かれます.
\begin{eqnarray} – \Delta \dot{V} (t, x) &=& \dot{V} (t, x) \, – \, \dot{V} (t, x+ \Delta x) \\ \rm{ } \\ &=& \dot{z} \Delta x \, \cdot \, \dot{I} (t, x) \; \cdots \; (2) \end{eqnarray}
(1), (2)式の両辺を \( \Delta x \) で割って, \( \Delta x \rightarrow 0 \) の極限を取れば, 偏微分の定義から以下の式が導かれます.
\begin{eqnarray} \left\{ \begin{array} \, – \frac{\partial}{\partial x} \dot{I} (t, x) &=& \dot{y} \, \dot{V} (t, x) \\ \, – \frac{\partial}{\partial x} \dot{V} (t, x) &=& \dot{z} \, \dot{I} (t, x) \end{array} \right. \; \cdots \; (3) \end{eqnarray}
時刻依存性の消去
(3)の連立偏微分方程式を解いていくわけですが, その前に (3)式の時刻依存性が邪魔なので消去します.
電流, 電圧の実効値 \( I \), \( V \) を用いると, フェーザ表示した電流 \( \dot{I} \), 電圧 \( \dot{V} \) は,
\begin{eqnarray} \left\{ \begin{array} \, \dot{I} (t, x) = I \, e^{ \, j \varphi _i } \, e^{ \, j \omega t} \\ \rm{ } \\ \, \dot{V} (t, x) = V \, e^{ \, j \varphi _v } \, e^{ \, j \omega t} \end{array} \right. \; \cdots \; (4) \end{eqnarray}
と表せます( \( \varphi _i \) は電流の初期位相, \( \varphi _v \) は電圧の初期位相, \( t \) は時刻). (3)式の両辺を \( e^{j \omega t} \) で割ると, (3)式中の時刻 \( t \) を消去できます.
\begin{eqnarray} \left\{ \begin{array} \, – \frac{ \mathrm{d} }{ \mathrm{d} x} \dot{I} (x) &=& \dot{y} \, \dot{V} (x) \\ \, – \frac{ \mathrm{d} }{ \mathrm{d} x} \dot{V} (x) &=& \dot{z} \, \dot{I} (x) \end{array} \right. \; \cdots \; (5) \end{eqnarray}
ここで, \( \dot{I} (x) = I \, e^{j \varphi _v} \), \( \dot{V} (x) = V \, e^{j \varphi _v} \) です.
以降の \( \dot{I} (x) \), \( \dot{V} (x) \) は, これまでの \( \dot{I} (t, x) \), \( \dot{V} (t, x) \) とは別のものになりますが, 便宜上同じ文字を使っています. ご注意ください.
方程式を解く 1(電信方程式の導出)
邪魔な時刻を無事に退けることができましたので, (5)式の片方をもう片方に代入して解いていきます.
\begin{eqnarray} \, – \frac{ \mathrm{d} }{ \mathrm{d} x} \left( – \frac{1}{\dot{z}} \, \frac{ \mathrm{d} }{ \mathrm{d} x} \, \dot{V} (x) \right) &=& \dot{y} \, \dot{V} (x) \\ \rm{ } \\ \frac{ \mathrm{d} ^2}{ \mathrm{d} x^2} \dot{V} (x) &=& \dot{z} \dot{y} \, \dot{V} (x) \end{eqnarray}
\( \dot{\gamma} ^2 = \dot{z} \dot{y} \) と置くと,
$$ \frac{ \mathrm{d} ^2}{ \mathrm{d} x^2} \, \dot{V} (x) = \dot{\gamma} ^2 \, \dot{V} (x) \; \cdots \; (6) $$
です.
同様の手順で, 電流についての式も導かれます.
$$ \frac{ \mathrm{d} ^2}{ \mathrm{d} x^2} \, \dot{I} (x) = \dot{\gamma} ^2 \, \dot{I} (x) \; \cdots \; (7) $$
(6), (7)式は, 流体力学や電磁気学に登場する波動方程式そのものです. 電気回路の分野では, これらを電信方程式(または伝送線路方程式)と呼びます.
方程式を解く 2(一般解の導出)
(6), (7)式の一般解は以下のように表されます.
\begin{eqnarray} \dot{V} (x) = A \, e^{- \dot{\gamma} x} + B \, e^{ \dot{\gamma} x} \; \cdots \; (8) \\ \rm{ } \\ \dot{I} (x) = C \, e^{- \dot{\gamma} x} + D \, e^{ \dot{\gamma} x} \; \cdots \; (9) \end{eqnarray}
面倒なので詳しい説明は省きますが, (8), (9)式を (6), (7)式に代入すれば, (8), (9)式が一般解となっていることが分かるはずです.
文字はもう少し減らすことができます. \( C \), \( D \) を \( A \), \( B \) を使って表すことを考えましょう.
(8)式を微分すると,
$$ \frac{ \mathrm{d} \dot{V} }{ \mathrm{d} x} = \; – \dot{\gamma} \, A \, e^{- \dot{\gamma} x} + \dot{\gamma} \, B \, e^{ \dot{\gamma} x } \; \cdots \; (10) $$
(5)式より, \( \dot{I} = \; – \frac{1}{\dot{z}} \, \frac{ \mathrm{d} \dot{V} }{ \mathrm{d} x } \) なので,
\begin{eqnarray} \dot{I} &=& – \frac{1}{\dot{z}} \, \left( – \sqrt{\dot{z} \dot{y}} \, A \, e^{- \dot{\gamma} x} \, + \, \sqrt{\dot{z} \dot{y}} \, B \, e^{ \dot{\gamma} x} \right) \\ \rm{ } \\ &=& \sqrt{ \frac{\dot{y}}{\dot{z}} } \, \left( A \, e^{- \dot{\gamma} x} \, – \, B \, e^{ \dot{\gamma} x} \right) \\ \rm{ } \\ &=& \dot{z}_0 ^{-1} \, \left( A \, e^{- \dot{\gamma} x} \, – \, B \, e^{ \dot{\gamma} x} \right) \; \cdots \; (11) \end{eqnarray}
ここで, \( \dot{z}_0 = \sqrt{ \frac{\dot{z}}{\dot{y}} } \) です.
(9)式と (11)式を比較すると,
$$ C= A \, / \dot{z}_0 \; , \; \; D = -B \, / \dot{z}_0 $$
であることが分かります. よって, 一般解は以下のように表されます.
\begin{eqnarray} \left\{ \begin{array} \, \dot{V} (x) &=& A \, e^{- \dot{\gamma} x} \, + \, B \, e^{ \dot{\gamma} x} \\ \, \dot{I} (x) &=& \dot{z}_0 ^{-1} \; \left( A \, e^{- \dot{\gamma} x} \, – \, B \, e^{ \dot{\gamma} x} \right) \end{array} \right. \; \cdots \; (12) \end{eqnarray}
\( A \), \( B \) を定めるためには 2つの境界条件が必要となります.
双曲線表示
電信方程式の一般解は, 双曲線関数で表すこともできます. こちらも導出してみます.
双曲線関数の定義から,
\begin{eqnarray} \left\{ \begin{array} \, e^{ \dot{\gamma} x} &=& \cosh{ \dot{\gamma} x} \, + \, \sinh{ \dot{\gamma} x} \\ \, e^{ – \dot{\gamma} x} &=& \cosh{ \dot{\gamma} x} \, – \, \sinh{ \dot{\gamma} x} \end{array} \right. \; \cdots \; (13) \end{eqnarray}
また, \( A+B = A^{\prime} \), \( B-A = B^{\prime} \) と置けば,
\begin{eqnarray} \left\{ \begin{array} \, \dot{V} (x) &=& A^{\prime} \cosh{ \dot{\gamma} x} + B^{\prime} \sinh{ \dot{\gamma} x} \\ \, \dot{I} (x) &=& – z_0 ^{-1} \; \left( B^{\prime} \cosh{ \dot{\gamma} x} + A^{\prime} \sinh{ \dot{\gamma} x} \right) \end{array} \right. \; \cdots \; (14) \end{eqnarray}
と表されます. 上記 (14)式が双曲線関数表示です. 指数関数表示でも双曲線関数表示でも意味するところは同じで, どちらも電圧(電流)を入力端からの距離 \( x \) の関数で表したものです.
指数関数表示と双曲線関数表示は用途によって使い分けましょう.
境界条件付き電信方程式
一般解である (12)式は 2つの未定定数( \( A \), \( B \) )を持ち, 特殊解を求めるためには 2つの境界条件が必要です. 以下では, 境界条件の簡単な場合について特殊解を考えてみます.
端点の電圧, 電流が分かっている場合
\( x=0 \) において, 電圧 \( \dot{V}_1 \), 電流 \( \dot{I}_1 \) とすると,
$$ \dot{V}_1 = A+B \; , \;\; \dot{I}_1 = \dot{z}_0 ^{-1} \, \left( A-B \right) $$
$$ A= \left( \dot{V}_1 + \dot{z}_0 \dot{I}_1 \right) /2 \; , \;\; B = \left( \dot{V}_1 -\dot{z}_0 \dot{I}_1 \right) /2 $$
よって,
\begin{eqnarray} \left\{ \begin{array} \, \dot{V} (x) &=& \frac{1}{2} \, \dot{V}_1 \, \left( e^{ \dot{\gamma} x} + e^{ – \dot{\gamma} x} \right) \, – \, \frac{1}{2} \, \dot{z}_0 \dot{I}_1 \, \left( e^{ \dot{\gamma} x} – e^{ – \dot{\gamma} x} \right) \\ \, \dot{I} (x) &=& – \frac{1}{2} \, \dot{z}_0 ^{-1} \dot{V}_1 \, \left( e^{ \dot{\gamma} x} \, – \, e^{ – \dot{\gamma} x} \right) + \frac{1}{2} \, \dot{I}_1 \, \left( e^{ \dot{\gamma} x} + e^{ – \dot{\gamma} x} \right) \end{array} \right. \; \cdots \; (15) \end{eqnarray}
これを双曲線表示すると,
\begin{eqnarray} \left\{ \begin{array} \, \dot{V} (x) &=& \dot{V}_1 \, \cosh{ \dot{\gamma} x} \, – \, \dot{z}_0 \dot{I}_1 \, \sinh{ \dot{\gamma} x} \\ \, \dot{I} (x) &=& – \dot{z}_0 ^{-1} \dot{V}_1 \, \sinh{ \dot{\gamma} x} \, + \, \dot{I}_1 \, \cosh{ \dot{\gamma} x} \end{array} \right. \; \cdots \; (16) \end{eqnarray}
となり, 少し見やすくなります.
さらに, 線路内に反射が存在しないことが分かっている場合は, もっと簡単に表すことができます.
\begin{eqnarray} \left\{ \begin{array} \, \dot{V} (x) &=& \, \dot{V}_1 \, e^{ – \dot{\gamma} x} \, \\ \, \dot{I} (x) &=& \, \dot{z}_0 ^{-1} \, \dot{V}_1 \, e^{ – \dot{\gamma} x} \, \end{array} \right. \; \cdots \; (17) \end{eqnarray}
反射については次の記事で詳しく説明します.
まとめ
以上, 分布定数回路でした.
後半は式変形ばかりで分かりにくかったかもしれません. 以下今回のまとめです.
- 微小区間を考えて連立微分方程式を解くと, 分布定数回路内の電圧・電流を入力端からの距離の関数で表せる(電信方程式).
- 電信方程式は, 双曲線関数で表すこともできる.
- 入力端にかかる電圧・電流が分かっている場合には, 解が 1つに定まり, 線路内の電圧・電流を決定できる.

