電信方程式：線路内の反射波について

前回は電信方程式の一般解を導出しました.

今回は解の中身を詳しく見つつ, 線路（分布定数回路）内で起きていることを見ていきます.

電信方程式の解は 2つの項の和で出来ており, それぞれ「入射波」, 「反射波」と呼ばれます.

なぜそう呼ばれるのか？そして, 反射波はどこから来るのか？が今回のメイントピックです.

復習：電信方程式とは

まずは前回記事（以下リンク）で導出したことを簡単にまとめていきます.

分布定数回路と電信方程式

架空線（いわゆる『電線』）や海底ケーブル, 同軸ケーブルなど, 内部を伝わる電圧（電流）の波形が, 部品（「ケーブル」など）のサイズと同程度である回路を扱うとき, 部品内部の電圧（電流）分布は一様ではなく, 高校までに習った回路の知識では太刀打ちできません.

高校までに習った回路は, 「回路内部の電圧（電流）波形が部品内部で線形と見なせるような回路」 =「集中定数回路」でした.

海底ケーブルのような「大きな」回路部品を扱うためには『分布定数回路』という考え方が必要となります.

分布定数回路とは, 有限値で有限個の回路要素で構成されるわけではなく, 回路要素が空間的に薄く広く分布している回路です. 例として, L, C, R で構成される均一な電線は以下のような分布定数回路として表されます.

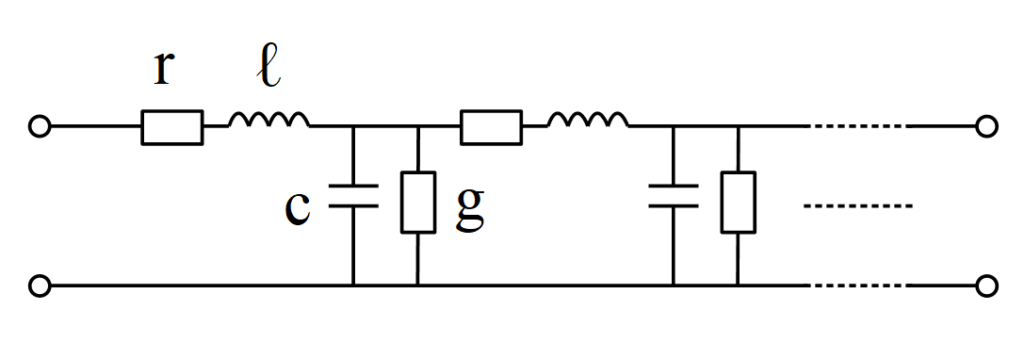
\(r , \ell , c , g \) はそれぞれ単位長さあたりの抵抗, インダクタンス, キャパシタンス, コンダクタンスです.

原点Oからの距離を \(x\) とすると, 分布定数回路内部の電圧 \( \dot{V} (x) \), 電流 \( \dot{I} (x) \) は以下の式を満たすことが導かれます.

\begin{eqnarray} \left\{ \begin{array} \, \frac{ \mathrm{d} ^2}{ \mathrm{d} x^2} \, \dot{V} (x) = \dot{\gamma} ^2 \, \dot{V} (x) \\ \, \frac{ \mathrm{d} ^2}{ \mathrm{d} x^2} \, \dot{I} (x) = \dot{\gamma} ^2 \, \dot{I} (x) \end{array} \right. \; \cdots \; (1) \\ \rm{ } \\ \rm{ } \, \left( \dot{\gamma} ^2 = \dot{z} \dot{y} \right) \end{eqnarray}

ここで, \( \dot{z}=r + j \omega \ell\), \( \dot{y}= g + j \omega c \) であり, \(j\) は虚数単位, \( \omega \) は入力電圧信号の角周波数です.

式(1) は電信方程式（telegraph equation, または伝送線路方程式）と呼ばれます.

式(1) の一般解は以下.

\begin{eqnarray} \left\{ \begin{array} \, \dot{V} (x) &=& \dot{A} \, e^{- \dot{\gamma} x} \, + \, \dot{B} \, e^{ \dot{\gamma} x} \\ \, \dot{I} (x) &=& \dot{z}_0 ^{-1} \; \left( \dot{A} \, e^{- \dot{\gamma} x} \, – \, \dot{B} \, e^{ \dot{\gamma} x} \right) \end{array} \right. \; \cdots \; (2) \\ \rm{ } \\ \rm{ } \, \left( \dot{z}_0 = \sqrt{ \dot{z} / \dot{y} } \right) \end{eqnarray}

一般解の表し方は指数関数型と双曲線関数型がありますが, ここでは指数関数型で表しています.

\(\dot{z}_0\) は「特性インピーダンス」という名前が付けられており, 後で大事になる概念です.

また, \( \dot{\gamma} \) （伝搬定数）を \( \dot{\gamma} = \alpha + j \beta\) （\(\alpha, \beta\) は実数）と分解して, \(\alpha\) を減衰定数, \(\beta\) を位相定数 と呼びます.

ここまで復習でした.

入射波と反射波

電信方程式は時刻に依存しません. 原点からの距離のみで電圧・電流の波形を表したものです.

時刻を加えたものが以下になります.

\begin{eqnarray} \left\{ \begin{array} \, \dot{V} (t, x) &=& \, \left( \dot{A} \, e^{- \dot{\gamma} x} \, + \, \dot{B} \, e^{ \dot{\gamma} x} \right) \, e^{j \omega t} \\ \, \dot{I} (t, x) &=& \dot{z}_0 ^{-1} \; \left( \dot{A} \, e^{- \dot{\gamma} x} \, – \, \dot{B} \, e^{ \dot{\gamma} x} \right) \, e^{j \omega t} \end{array} \right. \; \cdots \; (3) \end{eqnarray}

注意して頂きたいこととして, 電信方程式中の電圧, 電流はすべてフェーザ表示です. よって, 現実世界で観測される電圧, 電流の形を表しているわけではありません.

現実世界で観測される電圧・電流は, \(\dot{A}=|\dot{A}| \, e^{j \phi _{\dot{A}} }, \dot{B}=|\dot{B}| \, e^{j \phi _{\dot{B}} }, \dot{z}_0 =| \dot{z}_0 | \, e^{j \theta}\) とすると, 以下のように表されます.

\begin{eqnarray} \left\{ \begin{array} \, V (t, x) &=& \, \sqrt{2} \, |\dot{A}| \, e^{- \alpha x} \, \cos{ \left( \omega t – \beta x + \phi _{A} \right) } \\ &\rm{ }& + \sqrt{2} \, |\dot{B}| \, e^{ \alpha x} \, \cos{ \left( \omega t + \beta x + \phi _{B} \right) } \\ \, I (t, x) &=& \sqrt{2} \, |\dot{A} / \dot{z}_0 | \, e^{- \alpha x} \, \cos{ \left( \omega t – \beta x + \phi _A – \theta \right) } \\ &\rm{ }& – \sqrt{2} \, |\dot{B} / \dot{z}_0 | \, e^{ \alpha x} \, \cos{ \left( \omega t + \beta x + \phi _B – \theta \right) } \end{array} \right. \; \cdots \; (4) \end{eqnarray}

現実世界の波形とフェーザ表示の関係について詳しくは以下をご参照ください.

正弦波のフェーザ表示（複素数表示）

ここからは, 波形を視覚的に見ていきたいので, フェーザ表示ではなく, 三角関数で波を表していきます. フェーザ表示された複素電圧との混同を避けるために, 現実世界で観測される電圧, 電流については, \(V, I\) とドットなしで表記しました.

また, 電流も電圧も似たような形をしているので, 考えるのは電圧のみに限定しましょう.

式 (4) を見ると, 分布定数回路内部の電圧は 第1項 \(\sqrt{2} \, |\dot{A}| \, e^{- \alpha x} \, \cos{ \left( \omega t – \beta x + \phi _A \right) }\) と 第2項 \(\sqrt{2} \, |\dot{B}| \, e^{ \alpha x} \, \cos{ \left( \omega t + \beta x + \phi _{B} \right) }\) の波の足し合わせで表されることが分かります.

とある時刻における電圧の第1項, 第2項を, 位置 \(x\) に対して表示すると, それぞれ以下のような形になります.

また, 電圧の第1項の時間変化を追ってみたいと思います.

電圧の第1項について, \(x\) 軸に原点からの距離 \(x\), \(y\) 軸に電圧の瞬時値を取り, 時刻を変化させながら波の形状を追っていくと以下のようになります.

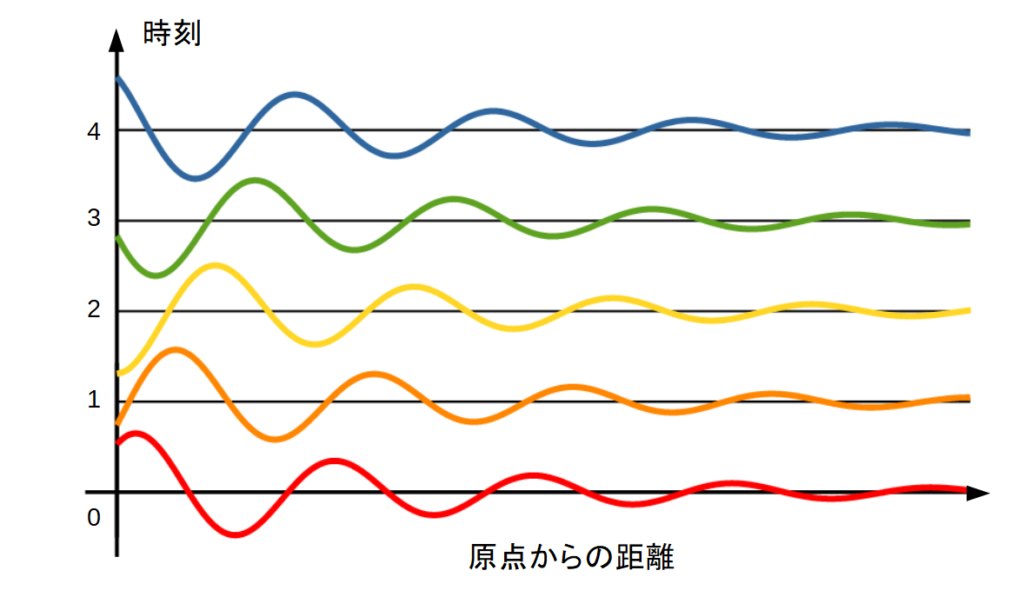
時間経過に対し, 波形は \(x\) の正の向きに移り行くことがお分かり頂けたでしょうか. このことから第1項は「入射波」もしくは「前進波」と呼ばれます.

一方, 第2項について, 先ほどと同様の軸を取って表示すると, 以下のようになります.

こちらは時間経過に対して \(x\) の負の向きに移動していることが分かるかと. この波を「反射波」と呼びます. 「後退波」とはあまり呼ばないようです.

以上まとめると, 均一な分布定数回路の中を伝搬する電圧は, 前進する波と後退する波の足し合わせになっていることが分かります.

線路定数の意味

三角関数で表された波の式を眺めると, 線路定数 \(\alpha, \beta, \dot{z}_0\) が物理的に何を意味するか, が分かってきます.

\(\alpha\) は波（入射波 or 反射波）が単位距離進んだとき, 波の振幅がどれだけ減衰するか, を表します. そのため, 名前もそのものズバリ, 減衰定数です.

\(\beta\) は波の初期位相を決めます. こちらもそのままです.

\(\dot{z}_0\) （特性インピーダンス）の定義は均一な分布定数回路内部における 「（単位長さあたりのインピーダンス / 単位長さあたりのアドミタンス）の 1/2乗」 です.

$$ \dot{z}_0 = \left( \dot{z} / \dot{y} \right) ^{1/2} \; \cdots \; (5) $$

また, 特性インピーダンスの大きさは 「線路内のとある位置における電圧と電流の大きさの比」になっています.

$$ | \dot{z}_0 | \, = \, | \dot{V} (x) | \, / \, | \dot{I} (x) | \; \cdots \; (6) $$

「結局, 特性インピーダンスとは何なのか」 という問いに一言で答えることは難しいのですが, 大まかに言えば, 「線路内のある一点における電圧と電流の比」と言えるかと. もちろんこれは正確な表現ではありません.

特性インピーダンスは「反射」や「整合」を考えるときに大切になります. どう大事になるのか, 以下で解説します.

数式で眺める反射波

電信方程式の一般解は入射波と反射波の足し合わせであることが分かりましたが, では, 反射波はどのように生じるのでしょうか？

任意点の反射係数とインピーダンス

ここからは簡単のため, 再びフェーザ表示で考えていきます.

反射波について考えるため, 反射係数 \(\dot{m}\) を導入しましょう. 反射係数 \(\dot{m}\) は, とある地点 \(x\) における電圧の入射波と反射波の大きさの比で定義される複素数です.

$$ \dot{m} (x) = \frac{\dot{B} \, e^{ \dot{\gamma} x}}{\dot{A} \, e^{- \dot{\gamma} x}} = \frac{\dot{B}}{\dot{A}} \, e^{2 \dot{\gamma} x} \; \cdots \; (7) $$

反射係数の大きさが 1 より大きいということは反射波の大きさの方が入射波より大きい場合を表し, 1 より小さいということは反射波の方が小さい場合を表します. また, \(\dot{m} (x) =0\) とは, 反射波が存在しないことを表します.

式 (2) より, 電流の反射係数は \( – \dot{m} (x) \) です.

また, 任意点のインピーダンス \(\dot{z} (x)\) を以下のように定めます.

$$ \dot{z} (x) = \frac{\dot{V} (x)}{\dot{I} (x)} = \frac{\dot{A} \, e^{- \dot{\gamma} x} \, + \dot{B} \, e^{ \dot{\gamma} x}}{\dot{A} \, e^{- \dot{\gamma} x} \, – \dot{B} \, e^{ \dot{\gamma} x}} \, \dot{z}_0 \; \cdots \; (8) $$

線路内で反射が存在しない場合

式 (7), (8) より, 任意点における反射係数とインピーダンスの間には以下のような関係が成立します.

$$ \dot{m} (x) = \frac{ \dot{z} \, (x) \; – \dot{z}_0 }{ \dot{z} (x) \; + \dot{z}_0 } \; \cdots \; (9) $$

「線路（分布定数回路）の中に反射波が存在しない」を言い換えれば, 「すべての \(x\) について, \(m (x) =0\)」ということです. 式 (9) より, そうなるための必要十分条件は,

$$ \dot{z} (x) = \dot{z}_0 \; \cdots \; (10) $$

となることだと分かります. つまり, 線路内の各点におけるインピーダンスが特性インピーダンスと等しく, それがずっと続くような（均一な）線路内では, 反射が生じません.

負荷との反射：インピーダンスマッチング

次に, 均一な分布定数回路に任意の負荷を接続した場合を考えます.

ここでは終端（\(x=L\)）にインピーダンス \(\dot{Z}_T\) を接続した分布定数回路を考えましょう. つまり, 下図のような状態です.

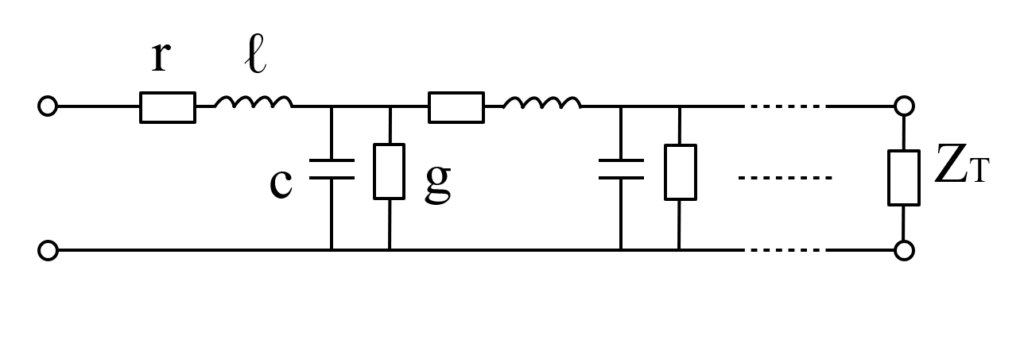
式 (9) より, 負荷を接続した点（\(x = L\)）におけるインピーダンスと反射係数の関係は以下のように表されます.

$$ \dot{m} (L) = \frac{\dot{Z}_T \; – \dot{z}_0 }{\dot{Z}_T \; + \dot{z}_0 } \; \cdots \; (11) $$

負荷が開放されている場合, \(\dot{Z}_T\) の大きさに比べて \(\dot{z}_0\) は無視できるほど小さいので, \(\dot{m} (L) = 1\) になり, 負荷が短絡されている場合には \(\dot{m} (L) = -1\) となります.

そして \(\dot{Z}_T = \dot{z}_0\) の場合には \(\dot{m} (L) = 0\) になります. このとき負荷は線路に「整合」していると言い, 線路と負荷が整合していると接続点において反射波が生じず, エネルギーを効率的に届けることができます.

「効率的なエネルギーの送信のために負荷を整合させること」を「インピーダンスマッチング」と呼びます.

テレビに信号を伝達する同軸ケーブルなどにおいてもケーブル内に反射波が生じないよう, ケーブルの特性インピーダンスとテレビの入力インピーダンスは 「\(50 \Omega\)」や「\(75 \Omega\)」 に統一されています.

まとめ

以上, 電信方程式と反射波についてでした. 今回の内容をまとめます.

1. 電信方程式の一般解は「入射波」と「反射波」の足し合わせになっている.
2. 反射波は入射波に対して逆向きに進む.
3. 均一な線路の内部では反射が生じない.
4. 「均一な線路の特性インピーダンス」と「その線路に接続された負荷のインピーダンス」が等しい場合, 接続点で反射は生じない.