分布定数回路におけるF行列の導出

本サイトではこれまで, 分布定数回路と電信方程式について話してきました.

電信方程式は, 偏微分方程式で, 波動方程式と似たような形をしています. つまり, 解くのが大変です.

この偏微分方程式にまつわる煩わしい計算を回避し, 回路接続の扱いを容易にするのが, 4端子行列, またの名を F行列です.

本稿では, 分布定数回路における F行列の導出方法を解説していきます.

分布定数回路

まずは分布定数回路についての復習です.

電線や同軸ケーブルに代表される, 「部品サイズが電気信号の波長と同程度か, それ以下」となる電子部品を扱うために必要となるのが, 分布定数回路という考え方です. 分布定数回路内では電圧や, 電流の密度が一定ではなく、オームの法則をそのまま適用することができません.

分布定数回路内の電圧 \( \dot{V} (x)\) , 電流 \( \dot{I} (x)\) は電信方程式によって記述されます.

\begin{eqnarray} \left\{ \begin{array} \, \frac{ \mathrm{d} ^2}{ \mathrm{d} x^2} \dot{V} (x) = \dot{\gamma} ^2 \, \dot{V} (x) \\ \, \frac{ \mathrm{d} ^2}{ \mathrm{d} x^2} \dot{I} (x) = \dot{\gamma} ^2 \, \dot{I} (x) \end{array} \right. \; \cdots \; (1) \\ \rm{ } \\ \rm{ } \, \left( \dot{\gamma} ^2 = \dot{z} \dot{y} \right) \end{eqnarray}

ここで, \(\dot{z}=r + j \omega \ell\), \(\dot{y}= g + j \omega c\) であり, \(j\) は虚数単位, \(\omega\) は入力電圧信号の角周波数, \(r, \ell, c, g\) はそれぞれ単位長さあたりの抵抗, インダクタンス, キャパシタンス, コンダクタンスです.

電信方程式の導出方法や, この式が意味するところの詳細については以下のリンクをご参照ください.

分布定数回路と電信方程式

電信方程式は, 電磁波を扱う「波動方程式」と似た形をしています. つまり, ケーブル中の電圧・電流の伝搬は, 空間を電磁波が伝わる場合と同じように考えられるということです. ただし, 電線は細長い形状をしているため, 1次元の波の伝搬と捉えられます.

入射波と反射波

電信方程式 (1) の一般解は以下のように表せます.

\begin{eqnarray} \left\{ \begin{array} \, \dot{V} (x) &=& \dot{A} \, e^{- \dot{\gamma} x} \, + \, \dot{B} \, e^{ \dot{\gamma} x} \\ \, \dot{I} (x) &=& \dot{z}_0 ^{-1} \; \left( \dot{A} \, e^{- \dot{\gamma} x} \, – \, \dot{B} \, e^{ \dot{\gamma} x} \right) \end{array} \right. \; \cdots \; (2) \\ \rm{ } \\ \rm{ } \, \left( \dot{z}_0 = \sqrt{ \dot{z} / \dot{y} } \right) \end{eqnarray}

電圧も電流も 2つの項の和で表されていて, \(\dot{A} \, e^{- \dot{\gamma} x}\) の項を入射波, \(\dot{B} \, e^{ \dot{\gamma} x}\) の項を反射波と呼びます.

分布定数回路内の反射波について詳しくは以下をご参照ください.

電信方程式：線路内の反射波について

入射波と反射波は進む方向が逆向きで, どちらも進むほどに減衰します.

双曲線関数型の一般解

式(2) では一般解を指数関数で表しましたが, 双曲線関数で表記することも可能です.

\begin{eqnarray} \left\{ \begin{array} \, \dot{V} (x) &=& \dot{A}^{\prime} \cosh{ \dot{\gamma} x} + \dot{B}^{\prime} \sinh{ \dot{\gamma} x} \\ \, \dot{I} (x) &=& – \dot{z}_0 ^{-1} \; \left( \dot{B}^{\prime} \cosh{ \dot{\gamma} x} + \dot{A}^{\prime} \sinh{ \dot{\gamma} x} \right) \end{array} \right. \; \cdots \; (3) \end{eqnarray}

\(\dot{A}^{\prime}\), \(\dot{B}^{\prime}\)は 式(2) に登場した定数と \(\dot{A}+\dot{B} = \dot{A}^{\prime}\), \(\dot{B}-\dot{A} = \dot{B}^{\prime}\) の関係を有します.

式(3) において, 境界条件が 2つ決まっていれば解を 1つに定めることが可能です.

仮に, 入力端の電圧, 電流がそれぞれ \( \dot{V} (0) = \dot{V}_{in} \, \), \(\dot{I} (0) = \dot{V}_{in}\) と分かっていれば, \(\dot{A}^{\prime} = \dot{V}_{in}\), \(\dot{B}^{\prime} = \, – \, \dot{z}_0 \, \dot{I}_{in}\) となるので, 入力端から距離 \(x\) における電圧, 電流は以下のように表されます.

\begin{eqnarray} \left\{ \begin{array} \, \dot{V} (x) &=& \dot{V}_{in} \cosh{ \dot{\gamma} x} \, – \, \dot{z}_0 \, \dot{I}_{in} \sinh{ \dot{\gamma} x} \\ \, \dot{I} (x) &=& \, – \dot{z}_{0} ^{-1} \dot{V}_{in} \sinh{ \dot{\gamma} x} \, + \, \dot{I}_{in} \cosh{ \dot{\gamma} x} \end{array} \right. \; \cdots \; (4) \end{eqnarray}

分布定数回路のF行列

以上復習でした. 以下, 今回のメインとなる 2端子対回路について話します.

2端子対回路

交流信号の取扱いを簡単にするために用いられるのが, 2端子対回路という考え方です. 2端子対回路では, 2つの端子で囲まれた領域をブラックボックスとし, 中身である回路構成要素については考えません. 入出力電圧と電流の関係のみを考察します.

2端子対回路を使えば, 分布定数回路の計算から微分方程式を排し, 行列計算で電流と電圧の関係を記述できるようになります.

早速, 電信方程式を 2端子対回路で置き換えていきましょう.

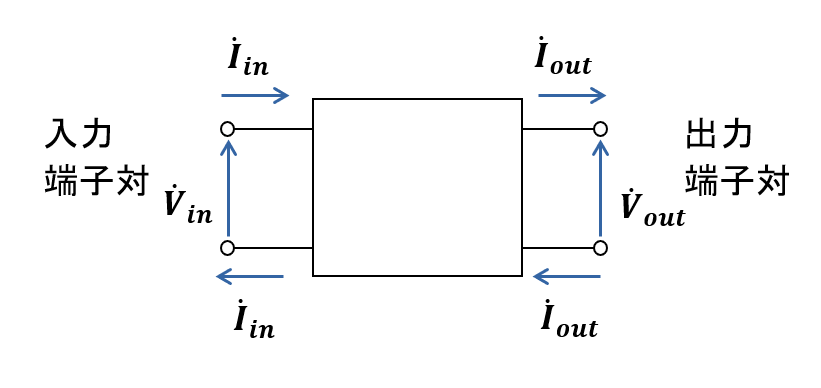
図1 において, 回路を構成する素子がすべて線形素子ならば, 入出力の電圧, 及び電流の関係は以下のように表されます.

\begin{eqnarray} \left[ \begin{array} \, \dot{V}_{in} \\ \, \dot{I}_{in} \end{array} \right] = \left[ \begin{array}{cc} \dot{F}_1 & \dot{F}_2 \\ \dot{F}_3 & \dot{F}_4 \end{array} \right] \, \left[ \begin{array} \, \dot{V}_{out} \\ \, \dot{I}_{out} \end{array} \right] \; \cdots \; (5) \end{eqnarray}

式(5) 中の \(F= \left[ \begin{array}{cc} \dot{F}_1 & \dot{F}_2 \\ \dot{F}_3 & \dot{F}_4 \end{array} \right]\) を 4端子行列, または F行列と呼びます.

2端子対回路や 4端子行列について, 詳しくは以下のリンクをご参照ください.

2端子対回路概説

分布定数回路のF行列

ここで, 改めて入力端の境界条件が分かっているときの電信方程式の解を眺めてみます.

\begin{eqnarray} \left\{ \begin{array} \, \dot{V} (x) &=& \dot{V}_{in} \cosh{ \dot{\gamma} x} \, – \, \dot{z}_0 \, \dot{I}_{in} \sinh{ \dot{\gamma} x} \\ \, \dot{I} (x) &=& \, – \dot{z}_{0} ^{-1} \dot{V}_{in} \sinh{ \dot{\gamma} x} \, + \, \dot{I}_{in} \cosh{ \dot{\gamma} x} \end{array} \right. \; \cdots \; (4) \end{eqnarray}

さらに, 線路の長さが \(L\) で, \(\dot{V} (L) = \dot{V}_{out} \) , \(\dot{I} (L) = \dot{I}_{out} \) とすると,

\begin{eqnarray} \left\{ \begin{array} \, \dot{V}_{out} &=& \dot{V}_{in} \cosh{ \dot{\gamma} L} \, – \, \dot{z}_0 \, \dot{I}_{in} \sinh{ \dot{\gamma} L} \\ \, \dot{I}_{out} &=& \, – \dot{z}_{0} ^{-1} \dot{V}_{in} \sinh{ \dot{\gamma} L} \, + \, \dot{I}_{in} \cosh{ \dot{\gamma} L} \end{array} \right. \; \cdots \; (6) \end{eqnarray}

式(6) を入力電圧 \(\dot{V}_{in}\) , 入力電流 \(\dot{I}_{in}\) について解くと,

\begin{eqnarray} \left\{ \begin{array} \, \dot{V}_{in} &=& \, \cosh{ \dot{\gamma} L} \, \dot{V}_{out} \, + \, \dot{z}_0 \, \sinh{ \dot{\gamma} L} \, \dot{I}_{out} \\ \, \dot{I}_{in} &=& \, \dot{z}_0 ^{-1} \, \sinh{ \dot{\gamma} L} \, \dot{V}_{out} \, + \, \cosh{ \dot{\gamma} L} \, \dot{I}_{out} \end{array} \right. \; \cdots \; (7) \end{eqnarray}

これを行列の形で表示すると, 以下のようになります.

\begin{eqnarray} \left[ \begin{array} \, \dot{V}_{in} \\ \, \dot{I}_{in} \end{array} \right] = \left[ \begin{array}{cc} \, \cosh{ \dot{\gamma} L} & \, z_0 \, \sinh{ \dot{\gamma} L} \\ \, \dot{z}_0 ^{-1} \, \sinh{ \dot{\gamma} L} & \, \cosh{ \dot{\gamma} L} \end{array} \right] \, \left[ \begin{array} \, \dot{V}_{out} \\ \, \dot{I}_{out} \end{array} \right] \; \cdots \; (8) \end{eqnarray}

式(8) を 式(5) と見比べて頂ければ分かる通り, \(\dot{V}_{in}\), \(\dot{I}_{in}\) が入力端の電圧と電流, \(\dot{V}_{out}\), \(\dot{I}_{out}\) が出力端の電圧, 電流と考えれば, 式(8) の \(2 \times 2\) 行列は F行列そのものです.

つまり、長さ \(L\) の分布定数回路の F行列は,

$$ F= \left[ \begin{array}{cc} \, \cosh{ \dot{\gamma} L} & \, \dot{z}_0 \, \sinh{ \dot{\gamma} L} \\ \, \dot{z}_0 ^{-1} \, \sinh{ \dot{\gamma} L} & \, \cosh{ \dot{\gamma} L} \end{array} \right] \; \cdots \; (9) $$

となります.

F行列は, 回路の接続を扱う上で大変便利なツールです. 均一な分布定数回路の F行列は常に式(9) の形で表されるので, 分布定数回路と他の回路が接続されているときは, 式(9) を使って, 回路の接続を計算することができます.

ちなみに, 今回は F行列の成分を双曲線関数で表しましたが, もちろん指数関数で表すことも可能です.

\( \dot{V} (0) = \dot{V}_{in} \, \), \(\dot{I} (0) = \dot{V}_{in}\), \(\dot{V} (L) = \dot{V}_{out} \) , \(\dot{I} (L) = \dot{I}_{out} \) を指数関数型の電信方程式の一般解に代入して整理すれば, F行列の成分は指数関数で表されます.

導出される F行列の成分は, 式(9) に, \( \cosh{\dot{\gamma}L}= \left( e^{\dot{\gamma L}}+e^{\dot{- \gamma L}} \right)/2 \), \( \sinh{\dot{\gamma}L}= \left( e^{\dot{\gamma L}}-e^{\dot{- \gamma L}} \right)/2 \) を代入したものと同じ値です.

まとめ

今回は, 均一な分布定数回路の F行列を導出しました. 分布定数回路と他の回路が接続されている場合にご活用ください.