有効電力と無効電力
交流回路では, 時刻に依存して電源が送り出す電力が変化します. また, 回路の構成によってエネルギーの授受効率が変わってくるため, 直流の場合とは異なる取り扱いが必要です.
これらを上手く扱うため, 「有効電力」・「無効電力」・「力率」という概念が用いられてきました.
本稿では, 交流電力の用語に関する解説記事です. 字面だけの定義ではなく, 本質的な理解を目指します.
Table of Contents
電力とは何か?
中学校で習ったことから一歩ずつ進めていきましょう. そもそも「電力」とは何なのでしょうか?
電力の単位 [ W(ワット)] は, エネルギーの単位である [ J(ジュール)] と, 時間の単位 [ s(秒)] を使って, 以下のように表せます.
\begin{eqnarray} [\rm{W}]=[\rm{J/s}] \end{eqnarray}
つまり, 1秒間に 1J のエネルギーを生み出すのが, 1W の電力です. 電力とは, 単位時間当たりに送達する電気エネルギーの量を表しています.
力学においては, 電力と全く同じ次元を持つ物理量として「仕事率」がありました. 単位時間あたりにどれだけの仕事(エネルギーの送達)をするのか, を表す量が仕事率です.
電力と仕事率の違いですが, 電力は「電荷」の運動によるエネルギー移動のみを取り扱います. 仕事率にはこのような縛りがなく, 「質量」を持つ物体の力学的エネルギー移動, 「磁束」の変化なども扱うことができます.
電圧と電流
電力が仕事率と対応しているように, 電圧や電流も, 力学における物理量と対応関係を考えることができ, 電圧は「力」, 電流は「速度」に対応します.
電圧とは電子を押し出す力, 電流とは電子の動く速度だと考えるとイメージが容易になります. もちろん, 厳密に言えば「電圧と力」, 「電流と速度」の単位の次元はそれぞれ異なりますので, あくまでイメージを容易にするための考え方とご理解ください.
力と速度は掛けると仕事率になりますが, 電圧と電流を掛けると電力になり, 仕事率と同じ次元になるところも似ています.
| 電気回路 | ⇔ | 力学 |
| 電力 [L2MT-3] | ⇔ | 仕事率 [L2MT-3] |
| 電圧 [L2MT-3I-1] | ⇔ | 力 [LMT-2] |
| 電流 [I] | ⇔ | 速さ [LT-1] |
エネルギーの供与・受取・消費・蓄積
ここから交流の話をします.
直流に比べ, 交流回路では考えるべきことが増えます. 具体的にどういった違いがあるのかを見ていきましょう.
瞬時電力と平均電力
直流回路においては, 電力は時刻に依存せず, 負荷が消費するエネルギーは常に一定です.
しかし, 交流回路においては負荷が消費するエネルギーが時刻に対して一定ではありません. そこで, 電力を考えるときには, ある瞬間における電力(瞬時電力)と, ある程度長い時間を平均した電力(平均電力)という概念が必要になってきます.
瞬時電力とは, 「ある時刻 \(t\) における電圧瞬時値と電流瞬時値の積」のことです.
\begin{eqnarray} p(t)=v(t) \cdot i(t) \; [\rm{W}] \end{eqnarray}
一方, 平均電力とは「瞬時電力の1周期分の平均値」を指します. 直流回路においては瞬時電力と平均電力が常に同じ値になりますが, 交流回路では2つは別物です. よって, 交流回路において「電力」を考える場合には, それが瞬時電力なのか, 平均電力なのかを常に考える必要があります.
消費する素子と蓄積する素子
抵抗は電気エネルギーを熱や光に変えて消費し, 回路全体の持つエネルギーを低減させます. 対して, 回路にエネルギーを供給するのが電源です. 抵抗によって失われたエネルギーを電源が供給することで, 回路全体のエネルギーはどの瞬間でも一定に保たれています.
一方, キャパシタやコイルは, 抵抗や電源と別の働きをします.
キャパシタは電源から送られる電気エネルギーを「電荷の位置エネルギー」に, コイルは「磁気エネルギー」にそれぞれ変換します. しかし, こうして蓄えられた電荷や磁界のエネルギーは, その周期の間に回路へと戻されます.
キャパシタやコイルによって生じた電界や磁界のエネルギーは回路外部の何かと相互作用をしない限り消費されません. こうした性質から, キャパシタやコイルなど, 一時的にエネルギーを蓄えるだけでエネルギーを消費しない素子を「蓄積素子」と呼びます.
電力の向き
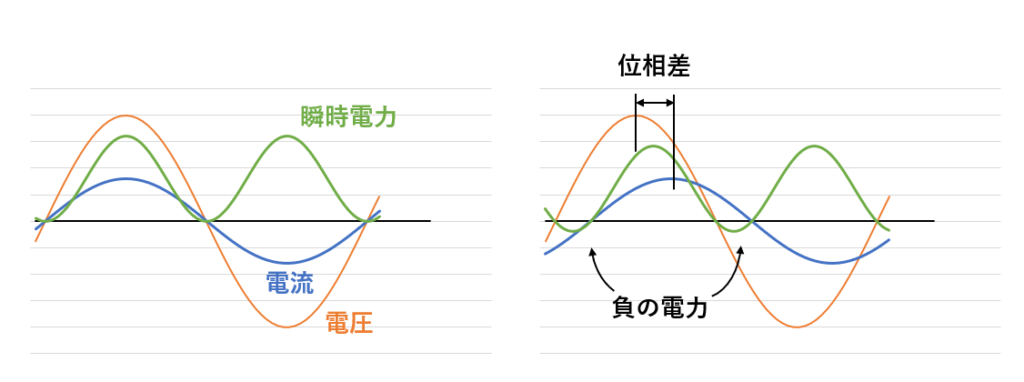
キャパシタとコイルは「エネルギーの蓄積と放出」を繰り返します. この蓄積と放出によって生じるのが, 「電圧と電流の位相のずれ」です.
電圧と電流の位相が揃っている場合, 電源が送り出す電力は常に正の値となります. しかし, キャパシタやコイルによって電圧-電流間の位相がずれると, 電源が送り出す電力が負になる瞬間が現れます.
「電源の送り出す電力が負になる」ということは, 電源が電力を受け取るということを意味します. ここで受け取っている電力は, キャパシタやコイルが電界や磁界として蓄えていたエネルギーです.
有効電力
平均電力は, 「有効電力」や「実効電力」とも呼ばれます. 有効電力という名称は, 後述する「無効電力」と対応したものです.
実際に, 交流回路における有効電力を求めてみましょう.
電圧瞬時値, 電流瞬時値をそれぞれ以下のように置きます.
\begin{eqnarray} v=\sqrt{2}V \sin{(\omega t- \phi)} \;\; [\rm{V}]\end{eqnarray}
\begin{eqnarray} i=\sqrt{2}I \sin{(\omega t- \phi -\theta)} \;\; [\rm{A}] \end{eqnarray}
ここで \(V\), \(I\) はそれぞれ電圧と電流の実効値, \(\omega\) は角周波数, \(\phi\) は初期位相, \(\theta\) は電圧と電流の位相差を表します. 簡単のため, 今回は正弦波を用います. 別の交流波形については考えません.
瞬時電力はこれらの積で表されるので,
\begin{eqnarray} p =vi &=& 2VI \sin{(\omega t- \phi)} \sin{(\omega t- \phi -\theta)} \\ &=& VI \cos{\theta}-VI \cos{(2\omega t-2\phi-\theta)} \;\; [\rm{W}] \end{eqnarray}
となります. 得られた瞬時電力の1周期分の平均値を取ると有効電力が得られるわけですが, 上式の第2項は角周波数\(2\omega\)の正弦波であるため, 平均すると零となり, 第1項のみが残ります. よって, 有効電力 \(P_e\) は,
\begin{eqnarray} P_e = VI \cos{\theta} \;\; [\rm{W}] \end{eqnarray}
です.
有効電力の式中に現れた \(VI\) と \(\cos \theta\) にはそれぞれ名前が付けられており, \(VI\) を「皮相電力」, \(\cos \theta\) を「力率」と呼びます.
力率は, どれだけ効率よく負荷に電力を届けられるかを表す指標です.
力率が小さいと, 負荷で同じ仕事をするにしても, 電源が送り出す電力は余計に大きくなければなりません. 送電する場合, 電流が大きいとその分だけ電力損失が大きくなります. よって, 電力損失を抑えるためには, 力率をできるだけ大きくすることが重要です.
また, 「電源から負荷へ効率よく電力を届ける指標」が力率である, ということを考慮すれば, 力率は負にならないことが分かります. 力率が負になるといういうことは, 電源が継続的にエネルギーを受け取る, ということであり, それは最早電源ではないからです.
また, 蓄積素子であるキャパシタやコイルは電力を消費せず, 電力消費は抵抗で起きているということを考慮すれば, 有効電力とは「抵抗で消費される電力」と言い換えることもできます.
無効電力
上記瞬時電流を加法定理で展開すると次のようになります.
\begin{eqnarray} i=\sqrt{2} I \cos \theta \sin{(\omega t -\phi)}-\sqrt{2} I \sin{\theta} \cos{(\omega t -\phi)} \;\; [\rm{A}] \end{eqnarray}
右辺の第1項 \(i_1\) は電圧 \(v\) と同相, 第2項 \(i_2\) は電圧 \(v\) と直交する成分であることが分かります.
ここで瞬時電力を \(p=v(i_1+i_2)=vi_1+vi_2=p_1 + p_2\) として, \(p_1\) と \(p_2\) をそれぞれ求めてみましょう.
\begin{eqnarray} p_1=VI \cos\theta \left\{ 1-\cos{2(\omega t -\phi)} \right\} \end{eqnarray}
\begin{eqnarray} p_2=-VI \sin \theta \sin{2(\omega t -\phi)} \end{eqnarray}
\(p_1\), \(p_2\) はそれぞれ電圧と電流が同相である電力の成分, 及び電圧と電流の位相が直交する電力の成分です.
\(p_1\) について, 1周期分の平均を取ると有効電力 \(P_e\) と同じ値となり, 抵抗で消費される電力を表していることが分かります. 一方の \(p_2\) は平均値を取ると零となる電力であり, 位相が電圧と直交していることから, 蓄積素子に向かう電力であると理解できます.
\(p_2\) の係数である
\begin{eqnarray} P_r=VI \sin \theta \end{eqnarray}
は, 蓄積素子とのエネルギーのやり取りの大きさを表しており, 「無効電力」と呼ばれます.
有効電力が「抵抗で消費される電力」と見なすことができるのに対し, 無効電力とは「電源と素子の間を行ったり来たりするだけの電力」を表しています.
1点注意したいこととして, 無効電力は瞬時電力でも平均電力でもありません. 「電力の成分に付いている係数」なので, 『電力』という表記さえ正確とは言い難いものです.
また, 上記では有効電力を「交流電力の1成分の平均値」, 無効電力を「交流電力の1成分の係数」であると定義したため, よくよく見てみるとこの2つは対応していません.
両者を綺麗に対応させるためには, 有効電力の定義も無効電力に合わせるべきです. つまり, 有効電力を \(p_1\) の係数部分と定義します. このように定義すると
\begin{eqnarray} p=P_e \left\{ 1-\cos{2(\omega t -\phi)} \right\} – P_r \sin{2(\omega t -\phi)} \end{eqnarray}
となり, 瞬時電力, 有効電力, 無効電力の関係性を1つの式で表現することが可能です.
もちろん, どちらの定義でも有効電力の値は同じになります. 有効電力の定義は書籍によって異なりますのでご注意ください.
まとめ
ここまでご覧いただきありがとうございました.
有効電力, 無効電力というものをそれぞれ総括するならば,
・有効電力:交流回路における電力平均値. 1周期の中で抵抗によって消費される電力.
・無効電力:電源と蓄積素子の間を行き来するだけで, 抵抗によって消費されない電力の大きさ.
となります.
本稿は, サイトをご覧いただいた方から間違いをご指摘いただき, 新たに執筆しました. ご指摘いただけたことに, この場を借りて感謝申し上げます.

