正弦波のフェーザ表示（複素数表示）

正弦波とはその名の通り sin関数の形をした波のこと.

コイルやキャパシタという回路要素は入力された信号を微分, もしくは積分して出力するのですが, コイルやキャパシタを sin関数が通過すると cos関数になってしまい計算が煩雑になってしまいます.

そこで, 微分, または積分しても形の変わらない関数である指数関数を用い, 計算を簡単にします.

正弦波を指数関数と複素数で表現したものが, 「正弦波のフェーザ表示」です. 本稿では, 正弦波のフェーザ表示を導出していきます.

一点注意として, 本サイトではこれまで虚数単位に \( i \) を使ってきましたが, 今回は \( j \) を使います. 電気回路の話に近づいてきて, 今後どこかで電流 \( i \) と虚数単位がバッティングすることを回避するためです.

正弦波のベクトル表示

復習ですが, 正弦波の変位 \( a(t) \) は以下の形式で書き表せます.

$$ a(t) = A_m \, \sin \, ( \omega t + \varphi ) $$

ここで, \( A_m \) は波の振幅, \( \omega \) は角速度, \( t \) は時刻, \( \varphi \) は初期位相です.

正弦波を考えるとき, 下図のような「回転するベクトル」が理解の助けになります.

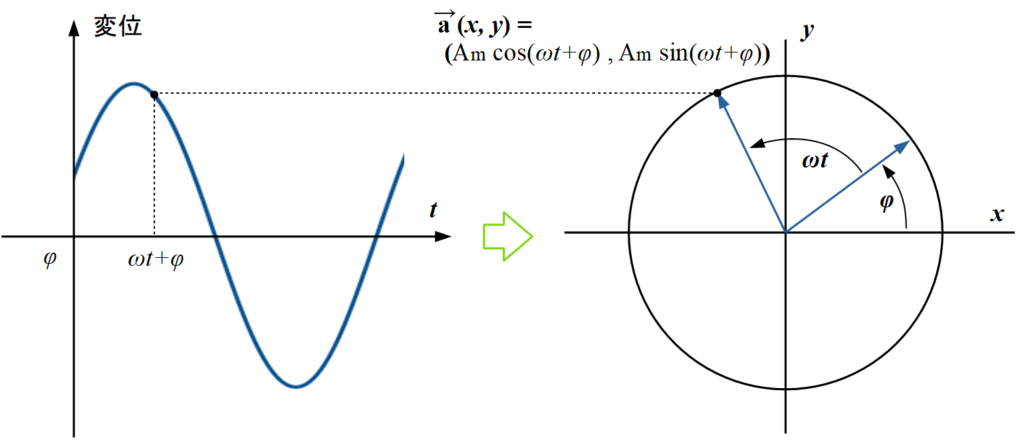
xy座標上に上右図のようなベクトル \( \overrightarrow{a} \) を配置すると, x軸と \( \overrightarrow{a} \) のなす角が位相（ \( \omega t + \varphi \) ）を表し, \( \overrightarrow{a} \) の y座標（すなわち, \( A_m \, \sin \, ( \omega t + \varphi) \) ）が時刻 \( t \) における波の変位を表します.

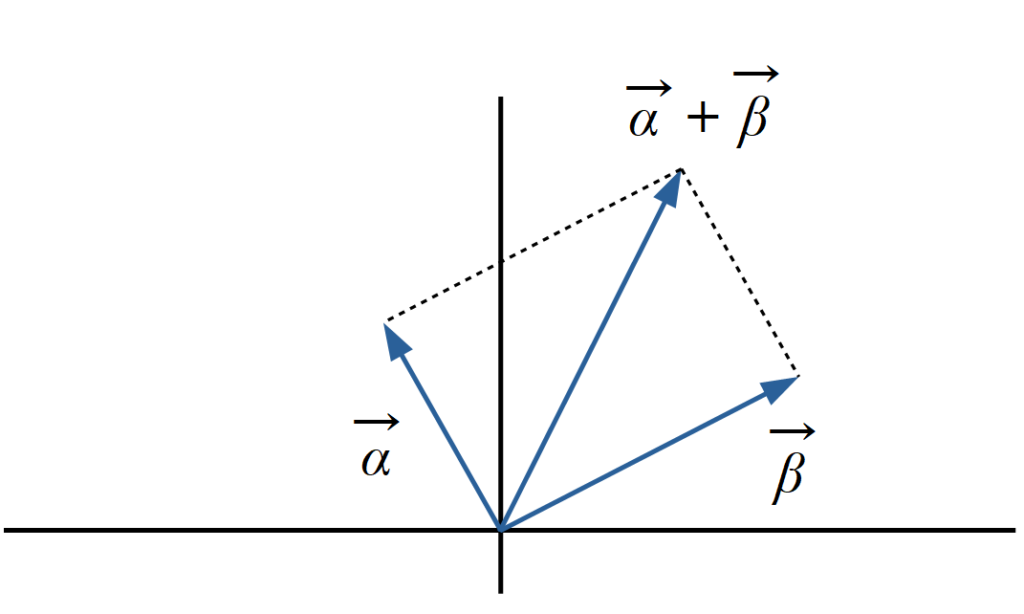
正弦波の変位をベクトルで置き換えると, 同じ角周波数の正弦波同士を足し合わせるときに大変便利です. 変位が \( \overrightarrow{ \alpha } \) の波と \( \overrightarrow{ \beta } \) の波を足し合わせた波の変位は \( \overrightarrow{ \alpha } + \overrightarrow{ \beta } \) になります. 図で描くとさらに分かりやすいです.

正弦波の複素数表示

複素平面上で回転するベクトル

上記の回転するベクトルのイメージにおきまして, 位置ベクトル \( \overrightarrow{a} \) は以下のように表せます.

$$ \overrightarrow{a} \, (x, y) = \left( A_m \, \cos \, ( \omega t + \varphi), \, A_m \, \sin \, ( \omega t + \varphi) \right) $$

x軸, y軸はこちらで勝手に決めた軸の名前なので, 本来何と呼ぼうと自由です. 横軸, 縦軸と呼んでもいいですし, 陽軸, 陰軸でも構いません.

数学の世界には回転を表すのに便利な座標系があります. 「実軸と虚軸」の2つの軸で張られる「複素平面」という座標系なのですが, 今回はこれを使って正弦波を表してみましょう.

複素平面については詳しくは → 複素平面と複素数の基本性質

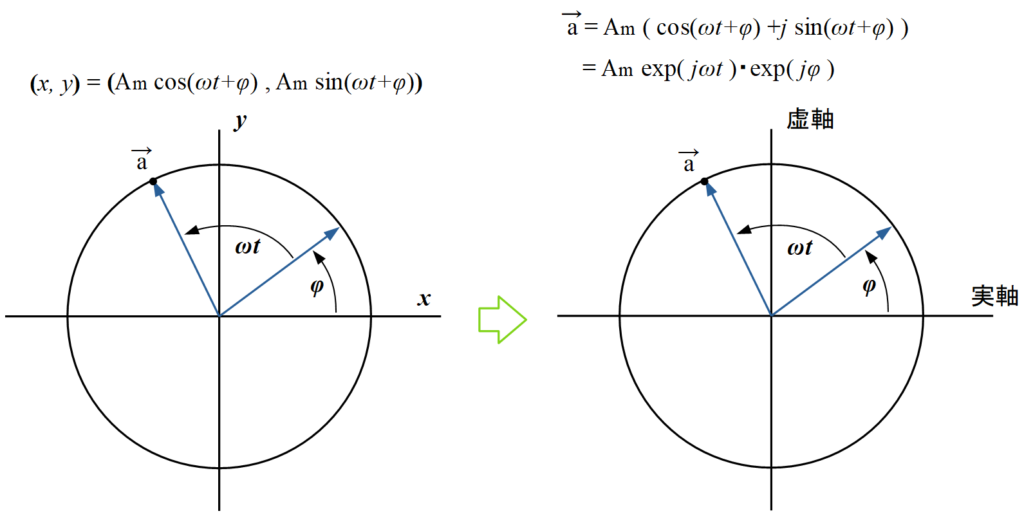
複素平面上にあるベクトル \( \overrightarrow{a} \) を複素形式で書くと, こうです.

$$ \overrightarrow{a} = A_m \, \cos \, ( \omega t + \varphi) + j \, A_m \, \left( \sin \, ( \omega t + \varphi) \right) $$

更に, 複素数の必殺技「オイラーの公式」を使って上式を書き換えると, こう.

$$ \overrightarrow{a} = A_m \, exp ( j \omega t ) \cdot exp ( j \varphi) $$

オイラーの公式について詳しくは → 複素指数関数の定義を考え、オイラーの公式を導出 (証明)する

上式における \( exp ( j \omega t ) \) を除いた

$$ \dot{a} = A_m \, exp ( j \varphi) $$

を「フェーザ」と呼び, このように正弦波を指数関数と複素数で表すことを「正弦波のフェーザ表示（複素数表示）」と呼びます.

正弦波の変位 \( a(t) \) とフェーザ表示した波は以下の関係にあります.

$$ a(t) = \mathrm{Im} ( \dot{a} \cdot exp ( j \omega t ) ) = \mathrm{Im} \left( A_m \, exp ( j \omega t ) \cdot exp ( j \varphi) \right) $$

フェーザ表示の利点

フェーザ表示はベクトル表示と同様に, 同じ角周波数の波ならば, 波の足し合わせを単純な複素数の足し算に帰着できるので便利です.

また, フェーザ表示最大の利点は, フェーザ表示した波の式を微分, もしくは積分したときに関数の形が変わらないことです. 計算がとても簡単になります.

導入でも述べたように, フェーザ表示した正弦波はコイルやキャパシタを通過しても形が変わりません.

こんなことやっていいのか問題

本稿では

1. 正弦波をベクトルで表す
2. ベクトルで表された正弦波を複素平面に置き換える
3. オイラーの公式で指数関数型に変換
4. \( exp ( j \omega t ) \) を除く

という流れでフェーザ表示を導出したわけですが, 特に 2. の部分でこんなことをやっていいのか, という疑問が生じるのは至極当然でしょう.

注意して頂きたいのは, 「フェーザ表示された波」と, 「元の波」は全く別のものである, ということです.

ここでは「三角関数の正弦波」と「複素平面上で回転するベクトル」という本来異なる 2つのものを一対一に対応させました. 「こう考えると矛盾が無いし, 便利だからこう考えることにしよう」という「提案」です.

「一対一に対応させた」というところを補足するために少し変な例を挙げますが、例えば, 「水 1g」と「水 1mL」は「水の密度が 1g/mL」であることを考慮すれば同じものを表していると言えるでしょう. しかし, 重さと体積は別次元のものですし, 同じ式の中で「水 1g + 水 1mL」ができないことは小学生のときに習った通りです.

このように, フェーザ表示した波も元の波と同じものを表していますが, 本来別のものです. 今回の導出過程は, 水の例で言えば, 「密度を使って体積を重さに変換する過程」と同じようなものだと考えればよいでしょう.

また 4. の部分では波の成分から時間依存性を排除しました. これはフェーザで波を扱う時（回路中の電気信号を扱う時など）に, 異なる周波数を持つ波が混在する場合がほとんど無いためだと私自身は理解しております.

以上のことから, 時間依存する（式中に \( t \)を含む）波とフェーザ表示された波を混在させて扱うことはできませんし, フェーザ表示の波だけであったとしても, 異なる周波数の波を混在させることはできません.

補：注意

今回, 正弦波が \( a(t) = A_m \, \sin \, \theta \) と表されるとき, フェーザ表示とは

$$ \dot{a} = A_m \, exp ( j \varphi) $$

のことである. と述べましたが, フェーザ表示を

$$ \dot{a} = \frac{1}{\sqrt{2}} \, A_m \, exp ( j \varphi) $$

と定義する場合もあります.

下の定義は「実効値」に対応しており, 複素電力を考えるときにはこちらの定義の方が計算が楽です. 故に分野によって定義が少々異なります.

「フェーザ」と言われたときは複素指数関数の前に付いている定数が何を表しているのか（振幅 or 実効値）に注意が必要です.

まとめ

正弦波のフェーザ表示を導出いたしました.

大変便利ですが, 複素数が入ってくるため理解が難しい概念です. フェーザ表示を理解が難しいときは図を眺めましょう.