複素数の使い方を忘れてしまったすべての大人達に贈る「複素数の基本性質」です. 複素数初学者も大歓迎. ここでは複素平面, 複素共役と絶対値について話していきます.
複素平面
複素平面とは, 複素数の実部を横軸, 虚部を縦軸に取り, 平面座標上に複素数を記述する幾何表現です.
こういうのは図で見るのが一番分かりやすいです. 下図をご覧ください.
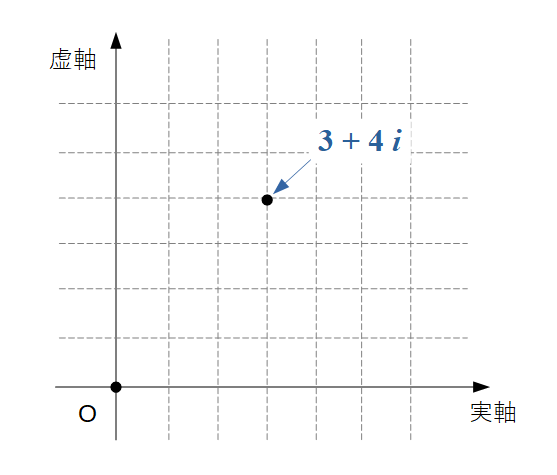
\( 3+4i \) という複素数は複素平面上で上図のように表されます. \(3+4i \) の実部は \( 3 \), 虚部は \( 4 \) です. この \( (3, 4) \) という組み合わせをxy座標上の点 \( (x, y) =(3, 4) \) と対応させます.
複素平面, という呼び方とは別に, 複素数平面, ガウス平面という呼び方もあります. 全部同じ意味です.
軸にも名前が付けられています. 横軸は「実軸」, 縦軸は「虚軸」です. 実軸上の点は虚部がゼロになっているため, すべて実数となり, 虚軸上の点は実部がゼロになっているため, すべて純虚数になります.
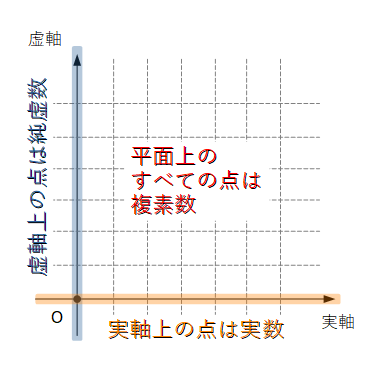
複素平面を考えることで, 以後の複素数に関する諸々を格段に考えやすくなりますし, 複素数や実数, 純虚数との関係が分かりやすくなります. 何より, イメージしにくい複素数を2次元平面上に視覚化することができるようになりました.
複素共役
続いて, 複素共役について解説します.
\( \dot{z}=a+bi \) ( \( a, b \) は実数)という複素数を考えまして, この複素数の虚部にのみ \( (-1) \) を掛けた数, つまり
$$ \overline{ \dot{z} } =a-bi $$
を \( \dot{z} \) の「複素共役」と呼びます. 読み方は「ふくそきょうやく」です.
中学校で, 「分母の有理化」というものを習ったと思いますが, 複素共役はこれに似ています.
\( \frac{1}{ a+ \sqrt{b} } \) ( \( a \) は有理数 \( , b \) は正の有理数) の分母を有理化するためには, \( \frac{1}{ a- \sqrt{b} } \) を掛ければ良いのでした.
$$ \frac{1}{ a+ \sqrt{b} } \times \frac{1}{ a- \sqrt{b} } = \frac{1}{ a^2 – b } $$
同じように, \( (a+b)(a-b) = a^2 -b^2 \) の公式を活用し, \( \overline{ \dot{z} } =a-bi \) という数を \( \dot{z} \) に掛けると, 目出度く虚数単位を消去することができます.
\begin{eqnarray} \dot{z} \times \overline{ \dot{z} } &=& (a+bi)(a-bi) \ &=& a^2 -b^2 \times i^2\ &=& a^2 +b^2 \end{eqnarray}
複素数の絶対値
複素数には, 実数に当然あるべきものがありません.
それは「大きさ」です. 複素数では数の大小を議論することができません.
ただし, 実数の絶対値という概念を拡張し, 複素数に適用することは可能で, 複素数 \( \dot{z} =a+bi \) の絶対値は以下のように定義されます.
$$ | \dot{z} | = \sqrt{a^2 + b^2}$$
実部と虚部をそれぞれ 2乗して足し, ルートを取ったものが, 複素数の絶対値です. 複素数の大小を比較することはできませんが, 複素数の絶対値ならば大小を比較することができます. 複素数の絶対値は複素平面上での原点からの距離に対応します.
また, \( a^2 +b^2 \) は \( \dot{z} \cdot \overline{ \dot{z} } \) でもあるので, 複素数の絶対値を以下のように表すこともできます.
$$ | \dot{z} | = \sqrt{ \dot{z} \cdot \overline{ \dot{z} }}$$
絶対値は複素数を扱う上で, よく出てきます.
まとめ
複素平面, 複素共役, 複素数の絶対値について解説しました.
