複素数, 虚数とは何か？複素数の歴史、虚数単位、複素数の分類

複素数 , 虚数とは？

高等学校で学ぶのは複素数の初歩のみ. これが何の役に立つのか, を高校で学ぶことはありません.

本サイトでは複素数の活用法, 何に利用されるのか, といったあたりに焦点を当てて解説していきたいと思います.

本稿では, 虚数の発見とその基本性質 (虚数単位 \( i \), 実部と虚部)について触れ, 複素世界に触れるための準備と致します.

虚数の歴史

研究者の間では数学自体を目的とする人もいますが, 少なくとも物理学者にとって, 数学とは物理をやっていくための道具です. 虚数も一種の道具であり, 必要だったからこそ発明され, 現代まで発展しました.

では, なぜ虚数を考える必要があったのか？何に必要だったのか？その辺りから.

数の歴史：自然数から無理数まで

人類が最初に知った数は「自然数」です.

自然数を使うことで「物の数を数えること」や「代金の計算」が可能になりました.

ただし,「物の長さ」を測ろうとしたときには問題が生じます. 長さが「目盛りと目盛りの間」にきてしまう. これでは正確な長さを決められません.

そこで考えたのが「小数と分数」です. どちらも「目盛りの間の数」を埋めることができ, より正確な測定が可能となりました.

このときは「長さはこれでよし. 分数を使えば表せない長さなど存在しない. 」そう思っていたことでしょう.

古代ギリシャではピタゴラス教団なる者たちがおりまして,「すべての数は有理数（分数）で表せる」ということを教義の一つとして信奉していました.

しかし, この教義の反例となるのが, 外ならぬピタゴラス自身が発見した「三平方の定理」です. 適当な直角三角形の2辺の長さを決め, 三平方の定理によって残りの1辺の長さを求めると, 辺の長さが分数では表せない場合があることが分かってきました.

教団はこの事実を長らく秘匿しますが, 結局「分数で表せない数」の存在を認めます.

「小数でも表せない数がこの世に存在するとは …. 致し方ない. 2回掛けて \( 2 \) となる数を \( \sqrt{2} \) と表すこととしよう. 小数でも分数でも書き表すことはできないから, 名前は『無理数』だ. 」

以上が紀元前400年頃の話です.

数の歴史：虚数

時は流れて16世紀. 代数学は大きく発展し, 三次方程式の一般解について活発に議論がなされていました.

3つの実数解を持つ3次方程式について解の公式を用いると, 式の途中で負の数の平方根を取る必要があります. 当時は負の数でさえまだ一般に認められていない時代.

「負の数の平方根などナンセンスだ. 何とかこれを回避できないものか」と考えてみるものの, 回避する術はありません.

「仕方ない. 実際には存在しない数だが,『負の数の平方根』を考えよう. 実際には存在しない数だから名前は『虚数』だ！！」

ということで, 以後「虚数」について考えられるようになりました. 発見された当初, 虚数は「解の公式を使ったときに出てきてしまうもの」という意味合いしかなかったのです.

後に虚数について色々と研究され, その有用性が知られることとなりましたが, 最初は「仕方なく導入した」ものでした.

歴史的に見れば, 無理数も虚数も「今までの数だけでは書き表せない数」を書き表すために「致し方なく生まれた」, と言えるでしょう.

複素数, 虚数とは何か？

複素数, 虚数, 純虚数, 虚数単位の定義は互いに重なり合い, 分かりづらいので, ここできっちりさせておきます. まずは虚数単位から見ていきましょう.

虚数単位

数の世界を複素数へと拡張するために「虚数単位 \( i \)」を導入します.

$$i^2 = -1$$

「2乗して \( -1 \) になる数」これが虚数単位 ( imaginary unit ) の定義です.

電気回路の分野では \( i \) と言えば「電流」ですので, \( i \) は電流に譲り, \( j \) で表すこともあります. 意味するところは同じです.

虚数単位を使うと, 虚数を以下のように表すことができます.

$$a+bi \;\; (a \rm{は実数}, \it{b} \rm{は} 0 \rm{でない実数})$$

あまり意識しないことではありますが, 2乗して \( a \) という \( 0 \) でない実数になる数は例外なく2つ存在しており, 虚数単位についても同様です. 即ち, 虚数単位は2つ存在します.

$$i = \pm \sqrt{-1}$$

複素数と虚数

複素数という用語と, 虚数という用語は「別物」なのですが, (昔の筆者のように) 同じものとして扱っている方も多いかと. 実部, 虚部という用語とともに, ちゃんとした定義を復習します.

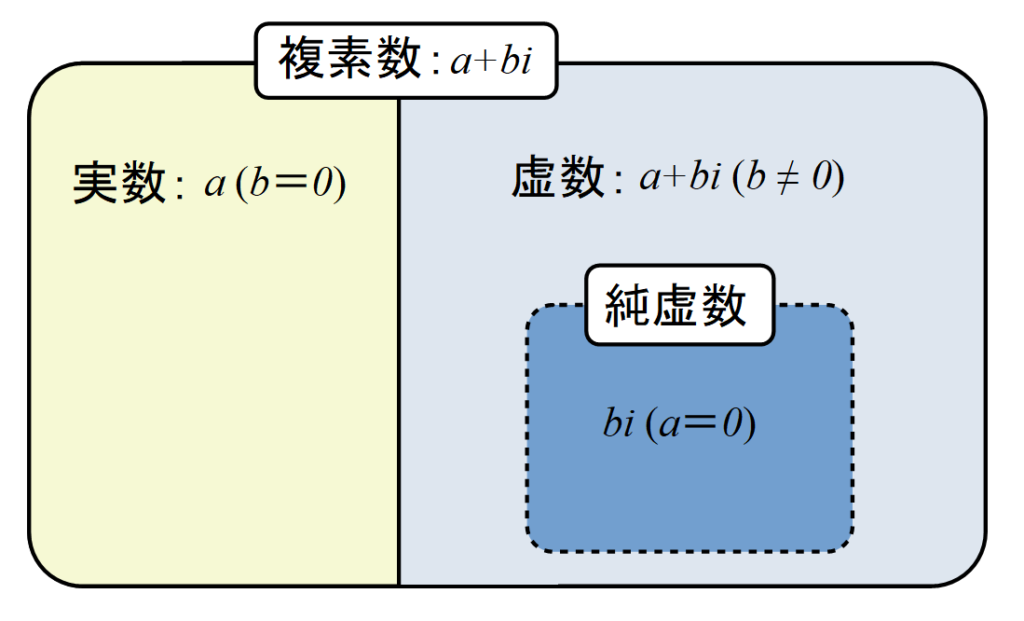
上図をご覧ください. 複素数, 実数, 虚数, 純虚数の関係を表しています.

複素数は,

$$a+bi \;\; (\it{a}, \it{b} \rm{ は実数} )$$

を満たす数です. つまり複素数は実数を包含します.

複素数の \( a \) のところを実部, \( b \) のところを虚部と呼びます.

一方の虚数とは先ほど述べたように, 以下を満たす数のことです.

$$ a+bi \;\; (b \neq 0 ) $$

純虚数の定義はこう.

$$ bi \;\; (b \neq 0) $$

虚数, 純虚数を日本語で説明すると以下のようになります.

厳密には複素数の定義はもっと広いようですが, 電子回路, 波動, フーリエ変換などをやっていくときに上記の定義の外側の複素数を考える必要はあまりないので, 一旦これでやっていきます. もっと厳密な定義が必要になったときには, そのとき考えることにしましょう.

以上です. 虚数と複素数のどちらがどちらなのか, 分からなくなった際には再びこのページを参照して頂ければ幸いです.

まとめ

複素数の基礎でした. 何か忘れてしまったときに使ってやってください.