複素数の極形式と回転

実空間における座標の表し方には, 直交座標表示と極座標表示がありますが, 複素数も, 直交座標で表す方法と極座標で表す方法があります.

複素数を極座標っぽく表すことを極形式と言い, 複素平面上の点の回転等々を考えるのに便利ですので, ここで解説していきます.

三角関数による複素数の表示 (極形式)

複素平面上に下図のような直角三角形OAZを考えます.

複素平面については前回記事で解説しています.

点Zは複素数 $\dot{z} =a+bi$ を表し, 点Aは点Zから実軸に引いた垂線の足なので, OAの長さは $\dot{z}$ の実部を表しています.

斜辺OZの長さを $r$, OZと実軸のなす角を $\theta$ とします.

このとき, 直角三角形OAZについて, 三角関数の定義から,

$$\begin{eqnarray} \cos{\theta} &=& a / r \\ \sin{\theta} &=& b / r \end{eqnarray}$$

です.

$a , b$ を $r$ と $\theta$ で表すと,

$$\begin{eqnarray} a &=& r \cos{\theta} \\ b &=& r \sin{\theta} \end{eqnarray}$$

よって, $z=r \, \left( \cos{\theta} + i \sin{\theta} \right)$ と表すことができ, これを複素数 $\dot{z}$ の極形式と呼びます.

また, 三平方の定理から, $a , b$ と $r$ の間には以下のような関係があることが分かります.

$$a^2 + b^2 = r^2 (\sin^2 \rm{\theta} + \cos^2 \rm{\theta}) = r^2$$

$$r = \sqrt{a^2 + b^2}$$

同様に, 逆三角関数を使うと, $\theta$ を以下のように表すことができます.

$$\frac{b}{a} = \frac{\sin{\theta}}{\cos{\theta}} = \tan{\theta}$$
$$\theta = \arctan{(b \, /a)}$$

回転

$\dot{z_1} = r_1 \, (\cos{\theta _1} +i \sin{\theta _1} )$ と $\dot{z_2} = r_2 \, (\cos{\theta _2} +i \sin{\theta _2} )$ という2つの複素数の掛け算について考えます.

$$\begin{eqnarray} \dot{z_1} \times \dot{z_2} &=& r_1 \times r_2 \times (\cos{\theta _1 + i \sin{\theta _1}}) \times (\cos{\theta _2} + i \sin{\theta _2}) \\ &=& r_1 r_2 \, \left( \cos{\theta _1} \cos{\theta _2} – \sin{\theta _1} \sin{\theta _2} + i \, (\sin{\theta _1} \cos{\theta _2} + \cos{\theta _2} \sin{\theta _1}) \right) \\ &=& r_1 r_2 \, \left( \cos{(\theta _1 + \theta _2) + i \sin{(\theta _1 + \theta _2)}} \right) \end{eqnarray}$$

となりました.

この計算結果を複素平面上で見てみましょう.

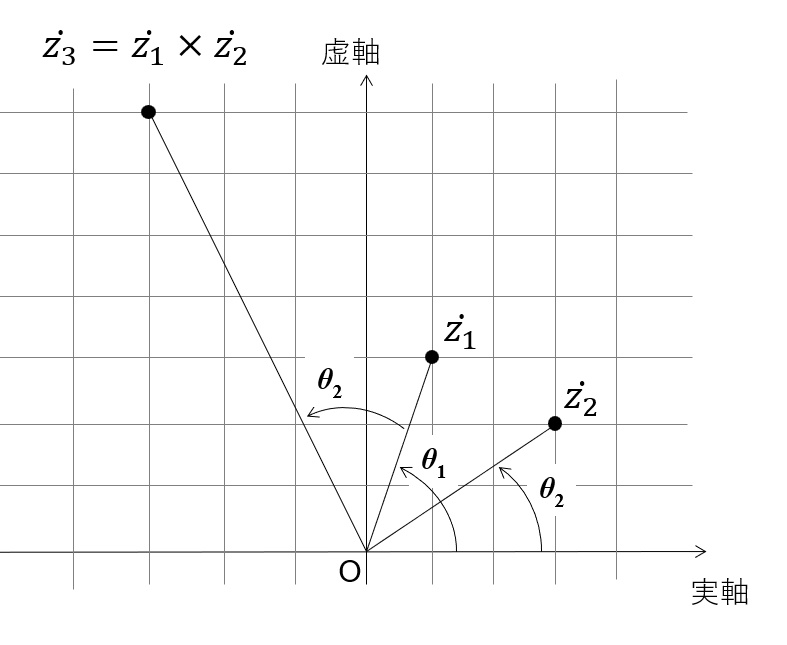
$\dot{z_1}$ と $\dot{z_2}$ の積を $\dot{z_3}$ とすると, 複素平面上の $\dot{z_3}$ の原点からの距離は $r_1 \times r_2$ となり, 位相は $\theta _1$ から $\theta _2$ 進んで, $\theta _1 + \theta _2$ となります. 複素数の掛け算は複素平面上の点の回転を表しているのです.

絶対値が $1$ である複素数を掛けた場合には, 位相のみが変化します. 位相が $0$ である複素数 (すなわち実数)を掛けた場合には, 位相は変化せずに原点からの距離のみが変化します.

まとめ

極形式を使って複素数を表すと, 複素数同士の積を「回転」として捉えることが可能です.