複素インピーダンスの表示:Cole-Cole plot と Bode plot
複素インピーダンスを図示する方法は特殊です. 普段論文などで図表を見慣れている人であってもこの分野の知識が無ければ混乱してしまうでしょう.
複素インピーダンスの図がややこしい理由は以下の3点に集約されます.
・なぜ図示する必要があるのかが曖昧であるため
・複素インピーダンスが「複素数」であるため
・図示する方法が複数あるため
以下では, この辺りに着目しつつ, 複素インピーダンスを図示する方法(Cole-Cole plot, Bode plot)について解説していきます.
Table of Contents
なぜ図示する必要があるのか
まず「なぜ複素インピーダンスを図示する必要があるのか」について話します.
「複素インピーダンス( \( \dot{Z} \) )」とは, 直流回路の「抵抗」に相当する概念であり, 複素数であることが特徴です.
回路に印加する交流電圧 \( \dot{V} \) と回路を流れる交流電流 \( \dot{I} \) をそれぞれ複素数表示(フェーザ表示)し, \( \dot{V} \) を \( \dot{I} \) で割ると求められます.
$$ \dot{Z} = \dot{V} / \dot{I} $$
詳しくはこちら:フェーザ表示の活用:複素インピーダンス
例として, 代表的な線形素子であるキャパシタと抵抗を並列接続した回路の複素インピーダンスは以下のように表されます.
$$ \dot{Z} = \left( 1/R + j \omega C \right)^{-1} $$
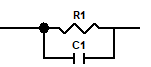
直流回路の合成抵抗と同様に, 並列接続した2つの素子の合成インピーダンスは「逆比の和」で計算できます. ここで, \( j \) は虚数単位, \( \omega \) は角周波数, \( R \) は抵抗の抵抗値, \( C \) はキャパシタの静電容量です.
\( \dot{Z} \) の中身を見て分かる通り, 複素インピーダンスは周波数に依存します. 同じ回路であっても周波数によって複素インピーダンスの値が変化するということです. 複素インピーダンスの値を知りたければ \( \dot{Z} \) の式に周波数を代入して計算しなければなりません.
しかし, 各周波数における複素インピーダンスの値が一目で分かる方法があります.
それが「複素インピーダンスの図示」なのです.
横軸に周波数を取り, 縦軸に複素インピーダンスを取ることで複素インピーダンスの周波数依存性が分かりやすくなります.
複素インピーダンスは複素数である
「縦軸に複素インピーダンスを取る」と申し上げましたが, 実際には「縦軸に複素インピーダンスを取る」ことはできません.
理由は皆さんお分かりのように, 「複素インピーダンスが複素数だから」です.
複素インピーダンスを1つのグラフで表現するためには, 周波数と垂直に2つの軸(実軸と虚軸, または \( | \dot{Z} | \) 軸と \( \theta \) 軸)を取り, 3次元のグラフを作らなければなりません.
最近は3次元のグラフを作成するソフトも充実しているので, 3次元のグラフを作っても構いません. しかし, 普段目にする「紙」や「pdf文書」に記載されているグラフが3次元であった場合, グラフを回転させて眺めることができないため見づらいです.
では「紙」や「pdf」などの2次元メディア上で複素インピーダンスを図示するためにはどうするか ? 「グラフを2つに分ける」ということになります.
Bode plot
2次元のグラフでは 「複素インピーダンス \( \dot{Z} \) – 周波数 \( f \)」という図が描けないことは先述の通りです.
そこで, 複素インピーダンス \( \dot{Z} \) を大きさ(\( | \dot{Z} | \))と位相( \( \theta \) )に分け, それぞれを周波数に対して表示することでグラフを 2つ作ります. これで複素インピーダンスを図示することができます.
このように複素インピーダンスを周波数に対して表示した図を Bode plot と呼びます. 例として, CR並列回路の Bode plot を以下に示します.
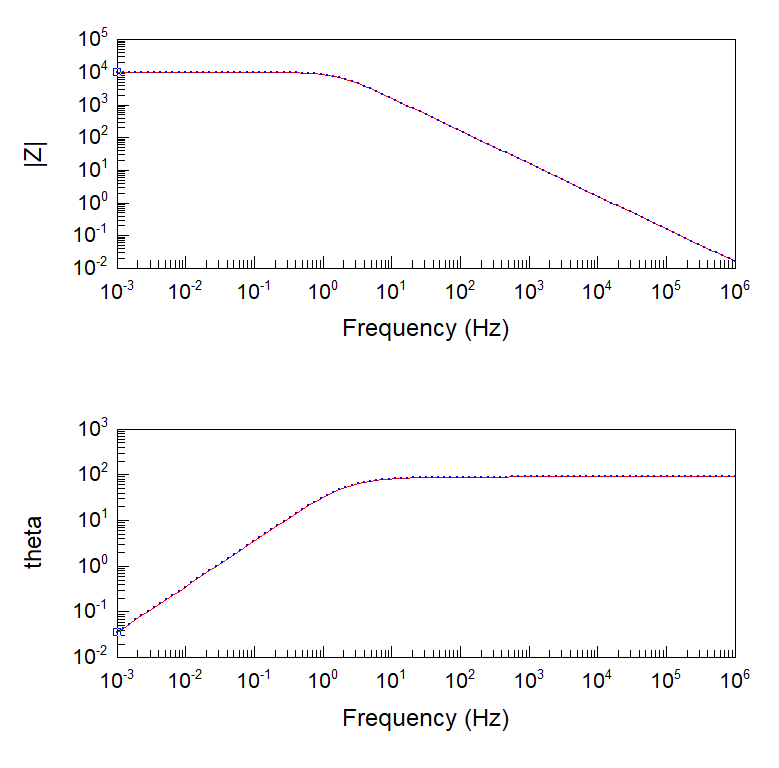
Bode plot の Bode は人の名前です. Bodeさんが考えました.
「縦軸として選ぶ2つ」は「複素インピーダンスの大きさと位相」を選ぶことが一般的ですが「2つセット」になっていれば複素インピーダンスの有する情報は一切失われないので, 縦軸の2つは「\( \dot{Z} \) の実部と虚部」でもいいですし, 「\( \dot{Z} \) の逆数の実部と虚部」でも構いません.
状況に応じて使い分けることが肝要です.
Cole-Cole plot
複素インピーダンスを表示する方法はもう1つあります. 名を「Cole-Cole plot」, 複素インピーダンスの表示を分かりにくくしている諸悪の根源です. もちろん使うと便利な所もあるのですが, 便利な所については後述することとし, 一先ず Cole-Cole plot とは何なのかについて話します.
Cole-Cole plot とは?
Cole-Cole plot とは, 複素インピーダンスの実部を横軸に, 虚部を縦軸に取った表示を指します.
兄 Kenneth S. Coleさんと, 弟の Robert H. Coleさんの共著論文の中で考案された表示法なので Cole-Cole プロットと呼びます. Nyquist plot という呼び名もありまして, Nyquist も人名です.
RC直列回路
RC直列回路の Cole-Cole plot を描いてみます.
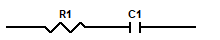
RC直列回路の複素インピーダンスは
$$ \dot{Z} = R + (j \omega C)^{-1} $$
なので, \( \mathrm{Re} \, ( \dot{Z} ) = R \), \( \mathrm{Im} \, ( \dot{Z} ) = -( \omega C )^{-1} \) です. これを図示すると
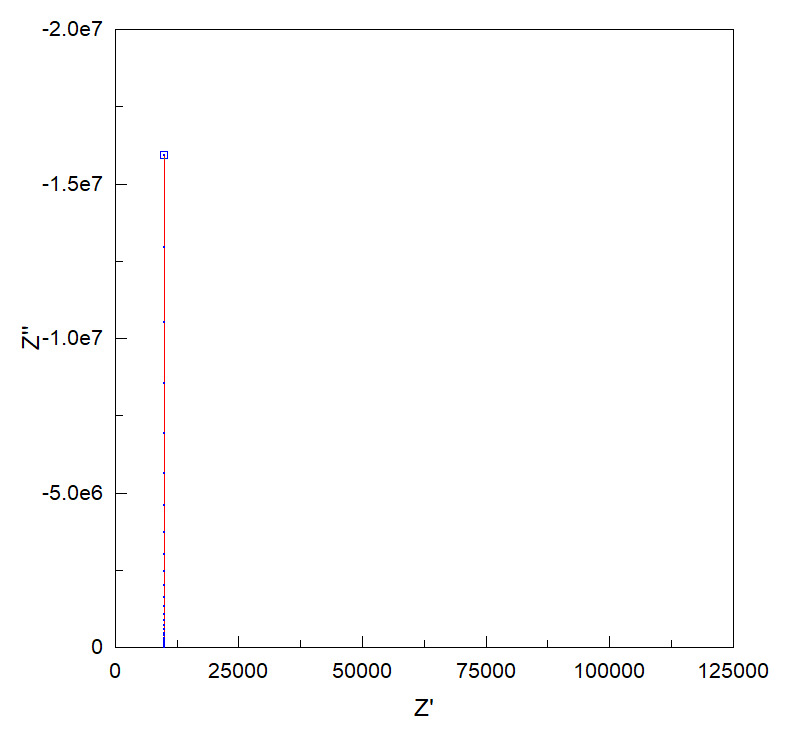
上記のように, ただの縦棒になりました. 図中 \( Z’ \) は複素インピーダンス実部, \( Z” \) は複素インピーダンス虚部を示しています. 縦軸は負の値を上にしているのでご注意ください.
Cole-Cole plot の大きな特徴として, 「周波数についての情報は消失」します. つまり, 図を見ただけでは「周波数 100 Hz のとき, 複素インピーダンスの値がいくらなのか」が分からなくなります.
RC並列回路
もう1つ例を挙げてみたいと思います. 先ほどは RC直列回路について Cole-Cole plot を描きましたが, 今度は RC並列回路の Cole-Cole plot を描いてみようと思います.
RC並列回路の複素インピーダンスは以下のように表されます.
$$ \dot{Z} = \left( 1/R + j \omega C \right)^{-1} = \left( \frac{1+ j \omega CR}{R} \right)^{-1} $$
よって,
\begin{eqnarray} \dot{Z} &=& \frac{R \, (1-j \omega CR)}{1+ \omega ^2 C^2 R^2 } \\ \rm{ } \\ \mathrm{Re} \, (\dot{Z}) &=& \frac{R}{1+ \omega ^2 C^2 R^2 } \; \cdots \; (1) \\ \rm{ } \\ \mathrm{Im} \, (\dot{Z}) &=& \frac{- \omega C R^2}{1+ \omega ^2 C^2 R^2} \; \cdots \; (2) \end{eqnarray}
上式から媒介変数 \( \omega \) を消去すると Cole-Cole plot を描けるので, 可能な限りスマートに \( \omega \) を消去します.
\( \omega CR \, \cdot \, \mathrm{Re} \, (\dot{Z}) = \mathrm{Im} \, (\dot{Z}) \) なので,
$$ \omega ^2 C^2 R^2 = \left( \frac{\mathrm{Im} \, (\dot{Z})}{\mathrm{Re} \, (\dot{Z})} \right)^2 \; \cdots \; (3) $$
(3)式を(1)式に代入すると \( \omega \) を消去できます.
$$ \mathrm{Re} \, (\dot{Z}) = \frac{R}{ 1+ \left( \frac{\mathrm{Im} \, (\dot{Z})}{\mathrm{Re} \, (\dot{Z})} \right)^2 } \; \cdots \; (4) $$
(4)式を整理すると,
\begin{eqnarray} 1+ \left( \frac{\mathrm{Im} \, (\dot{Z})}{\mathrm{Re} \, (\dot{Z})} \right)^2 &=& \frac{R}{\mathrm{Re} \, (\dot{Z})} \\ \rm{ } \\ \mathrm{Re} \, (\dot{Z}) ^2 + \mathrm{Im} \, (\dot{Z}) ^2 &=& R \, \cdot \, \mathrm{Re} \, (\dot{Z}) \\ \rm{ } \\ \left( \mathrm{Re} \, (\dot{Z}) -R/2 \right)^2 + \mathrm{Im} \, (\dot{Z}) ^2 &=& (R/2)^2 \; \cdots \; (5) \end{eqnarray}
これだけでも十分かもしれませんが, もっと分かりやすくするために, \( x = \mathrm{Re} \, (\dot{Z})\), \( y = \mathrm{Im} \, (\dot{Z}) \) と置きますれば,
$$ \left( x – R/2 \right) ^2 + y^2 = (R/2)^2 \; \cdots \; (6) $$
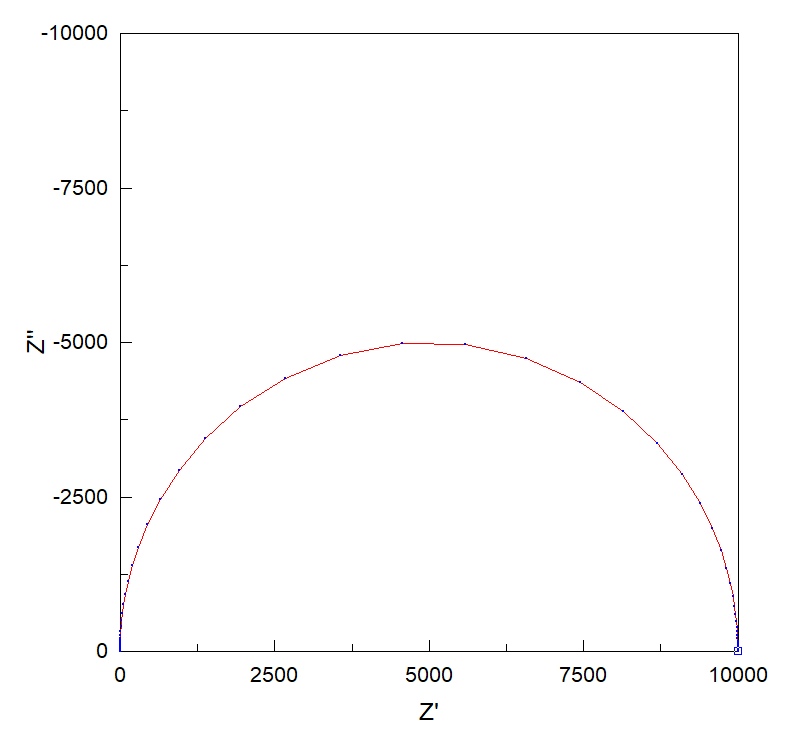
となり, 「円」の式を表していることが分かります. さらに言えば, \( y \) は常に負の値を取るので, (6)式が表しているのは「半円」です. RとCに適当な値を入れて図を描いてみると下のようになります.
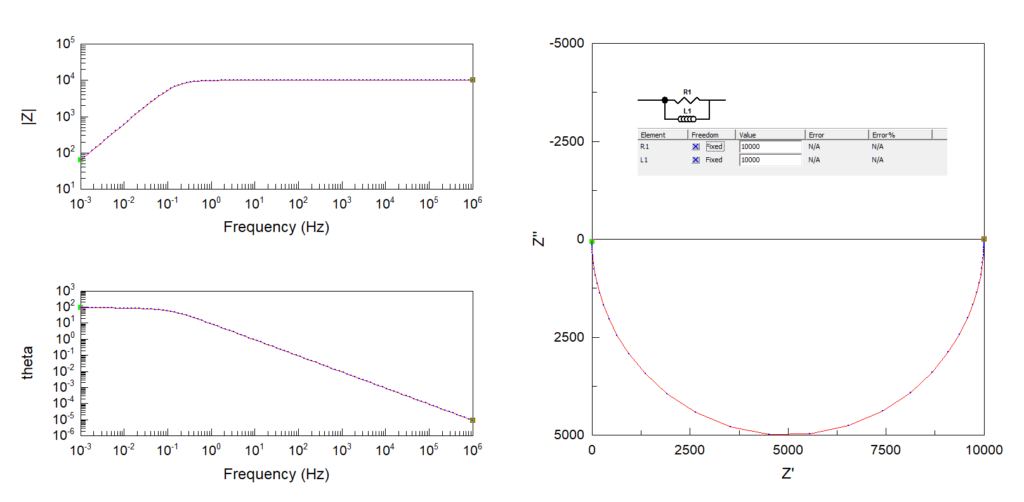
様々な回路の Bode plot と Cole-Cole plot
他の回路についても Bode plot, Cole-Cole plot を描いてみます.
複素インピーダンスを描くには ZView という便利なソフトがあり, 上記 plot も ZView で描いています. 無料でダウンロードできるので, この分野を学びたい人, 暇な人, 回路を使って模様を描きたい人はダウンロードしてみてください.
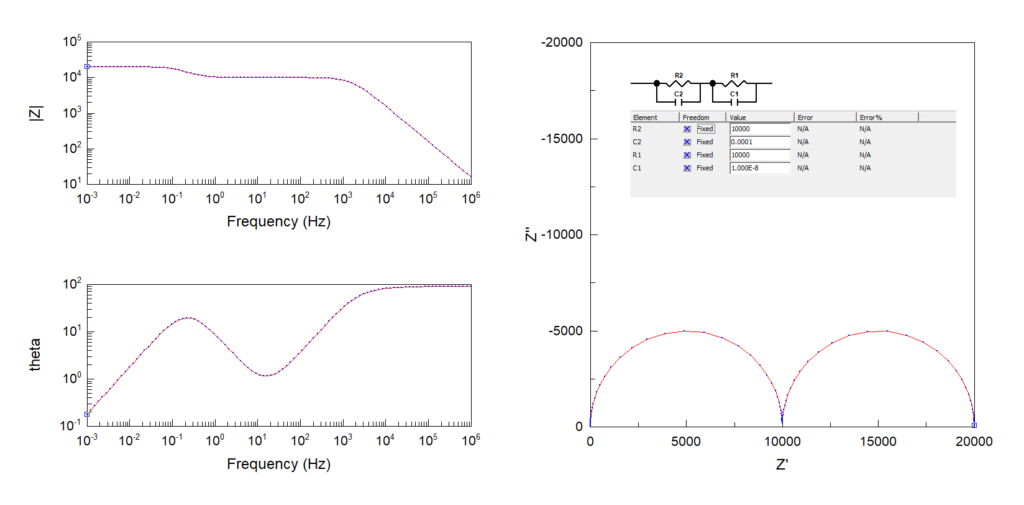
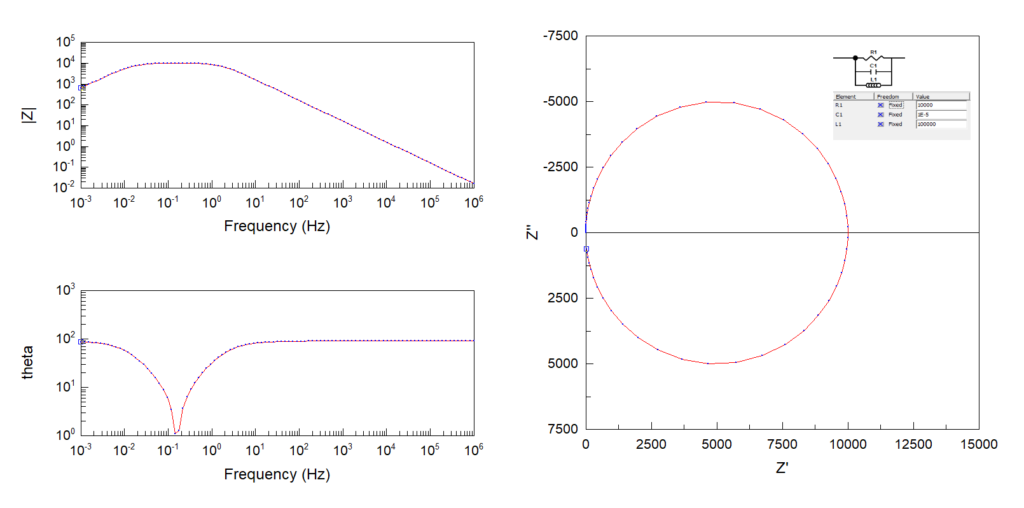
Cole-Cole plot の利点
Cole-Cole plot は周波数についての情報が失われ, 素人が見て理解するのも大変なのですが, 利点もあります.
それは「回路の形に起因して特徴的な構造が現れる」ことです.
・RC直列回路 → 虚部が負となる縦棒
・RL直列回路 → 虚部が正となる縦棒
・RC並列回路 → 虚部が負となる半円
・RL直列回路 → 虚部が正となる半円
・RLC並列回路 → 円
各回路で上記のような構造が現れ, それらが直列に接続されると円や縦棒が連なっていきます.
例えば, 以下の論文中で「電池の複素インピーダンスの周波数依存性」を測定していますが, 論文中の図を見ると, RC並列回路が3つ(図中のP1, P2, P3)存在することが分かります.
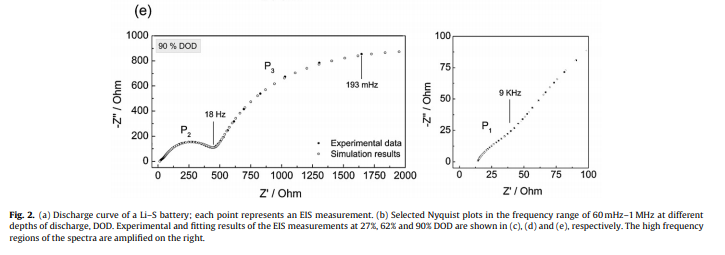
実際の測定結果においては, RC並列回路が別の RC並列回路と相互作用して円が歪んだり, 1つの円になってほとんど見えなくなったりしますが, これを解析すると電池の充放電過程に影響を及ぼす化学反応を数値化して比較できるわけです.
このように複素インピーダンスの Cole-Cole plot の解析は, 最近話題の電池分野でも重要な解析手法となっております.
まとめ
以上, 複素インピーダンスの表示についてでした.
複素インピーダンスは複素数であり, 周波数依存性を有するために理解が困難ですが, 複素インピーダンスを図示し, 可視化することで理解が容易になります.
複素インピーダンスを理解するためには, 自分で手を動かしてみることも効果的ですし, ZView のダウンロードは無料ですので, お時間あるときに試してみても良いかと.

