交流回路のためのグラフ理論基礎

これから何回かに渡って, 閉路方程式やテレゲンの定理, 相反定理について語っていきたいと思います.

しかし, それらを理解するためには, 「グラフ」という高校までに習わなかった考え方を導入せねばなりません. 簡単そうに見えて奥が深い分野です.

本稿は, グラフ理論とはどういうものなのか, という概形を掴むための記事になっています.

グラフとは？

「点」と「それらの点を繋ぐ線」からなる図形を「グラフ」と呼びます.

一般に, 数値を視覚化した図のことを「グラフ」と呼びますが, ここでは関係ありません.

グラフを構成する点は, 「節点・頂点・ノード」などと呼ばれ, 線は「枝・辺・エッジ」などと呼ばれます. 以降では, 「節点」と「枝」で統一させて頂きます.

理解を容易にするために例を挙げていきましょう.

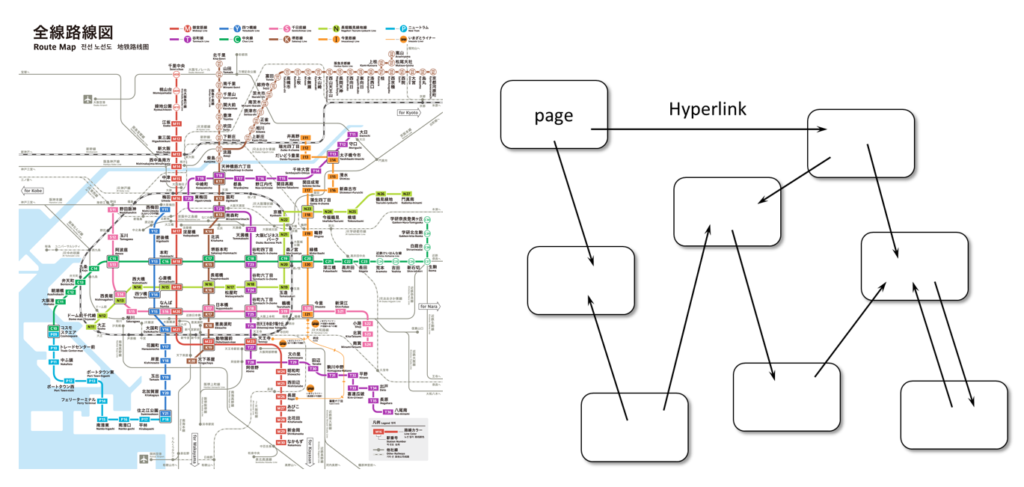
鉄道やバスの路線図は, 代表的なグラフです.

電車に乗っている乗客にとって最も重要な情報は, 「ある駅がどの駅に繋がっているか」ということであって, 線路の曲がりや勾配は重要ではありません. こうした「節点（駅）同士の繋がり」を見やすくするためには, グラフが適しています. グラフは, 路線の細かな情報をそぎ落とし, 「節点同士の関係」のみの図へと抽象化したものです.

他にも, ウェブページのハイパーリンクが作る「リンク・被リンクの関係性」は, しばしばグラフで表されます.

グラフにおいて, 枝の長さや, 節点の位置には一切意味がありません. そして, このグラフを数学的に取り扱おうとする試みが, グラフ理論という体系です.

有向グラフ

グラフには「有向グラフ」と「無向グラフ」の 2種類が存在します.

有向グラフとは, 枝が方向を持つグラフです. 無向グラフでは, 枝が方向を持ちません.

例えば, 路線図は無向グラフです. 電車は双方向に運行するため, 枝（路線）に特定の方向はありません.

対して, ハイパーリンクの「リンク・被リンクの関係図」は有向グラフで表されます. リンクは特定の向き（リンク元→リンク先）を持っているためです.

有向グラフで表される回路

電気回路は有向グラフで表すことができます.

下図2(左) のような回路は, 図2(右) のようなグラフで表されます. 回路をグラフで扱うと, 節点同士の関係が分かりやすくなり, キルヒホッフの電流則や電圧則を行列で表現できるようになります.

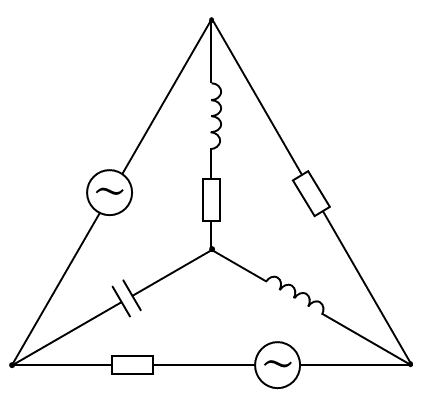
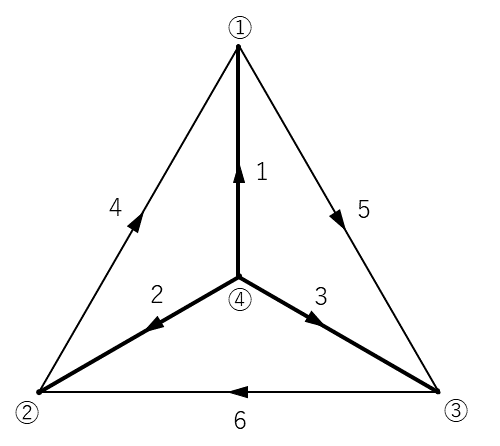
例として, 図2(右) のグラフについて, 電流則を書き表してみましょう. 図2(右) のように節点と枝に番号を付すと, 各節点における電流則の式は以下となります.

\begin{eqnarray} \, \begin{array}{cc} \, {\rm 節点①} &{\rm :}& i_1+i_4-i_5 = 0 \\ \, {\rm 節点②} &{\rm :}& i_2-i_4+i_6 = 0 \\ \, {\rm 節点③} &{\rm :}& i_3+i_5-i_6 = 0 \\ \, {\rm 節点④} &{\rm :}& – i_1-i_2-i_3 = 0 \end{array} \; \; \; \cdots \; (1) \end{eqnarray}

流れ込む電流に \( + \), 流れ出る電流に \( – \) を付しています.

また, 式(1) は, 次の行列 \(A\)

\begin{eqnarray} A = \begin{bmatrix} 1 & 0 & 0 & 1 & -1 & 0 \\ 0 & 1 & 0 & -1 & 0 & 1 \\ 0 & 0 & 1 & 0 & 1 & -1 \\ -1 & -1 & -1 & 0 & 0 & 0 \end{bmatrix} \; \cdots \; (2) \end{eqnarray}

と, 電流ベクトル \( \boldsymbol{i} = [ i_1 \cdots i_6 ] ^{\rm T} \) を用いて,

\begin{eqnarray} A \, \boldsymbol{i} \, = \, 0 \end{eqnarray}

と表すことができます. 電流ベクトルの右肩にある \({\rm T}\) は転置を意味する記号です. 式(1) と 式(2) を見比べることで, 行列 \(A\) の意味するところが何となく分かってくるかと.

例えば, 行列 \(A\) の第1行は節点1 に流入, または節点1 から流出する電流を表しています. 節点1 に対し, 枝1, 枝4 からは電流が流入し, 枝5 からは電流が流出します. そのため, 行列A の 1行の 1列と 4列は \(+1\), 5列は \(-1\) となっています. 他の行も同様です.

行列 \(A\) は各節点と枝の接続関係を表しているため, 「接続行列」と呼ばれます.

グラフの諸特性

以下では, 回路をグラフとして扱っていくときに重要となる用語と, 基本となるグラフの特性について解説します.

用語

今後使っていく用語を定義します.

パス：ある節点からスタートし, 同じ節点を 2度通ることなく, 別の節点へ到達するために通過する枝の集合.

閉路：ある節点からスタートし, 同じ節点を 2度通ることなく, 元の節点へ戻ってくるために通過する枝の集合.

連結：グラフ中の任意の 2節点に対して, 節点間を繋ぐパスが存在する状態.

木：すべての節点を連結する枝集合で枝の数が最小となる枝集合. 枝集合の選び方には任意性がある.

補木：木以外の枝の集合. 木の選び方に任意性があるため, 補木の枝のうちの 1つを木に加える場合, 木の枝の中から 1つが補木となる.

リンク：補木の枝のこと.

例として, 図2(右) のグラフは連結です. また, 図2(右) では, 枝1, 2, 3 の 3本の枝で木を構成し, 枝4, 5, 6 がリンクであると考えることができます.

木の選び方は一通りではなく, 例えば, 図2(右) で, 枝1, 5, 6 を木の枝とすることもできます. この場合, 枝2, 3, 4 がリンクです.

グラフの諸特性

上記, 木, リンク, 閉路の関係から, 以下の特性が導かれます.

（1） 木は閉路を含まない.

（2） 木に 1本のリンクを加えると閉路ができる.

（3） 木の最小性から, 木の枝を 1本取り除くと, 残りの節点と繋がらない節点が生じる.

この 3つの性質について, もう少し詳しく見ていきましょう.

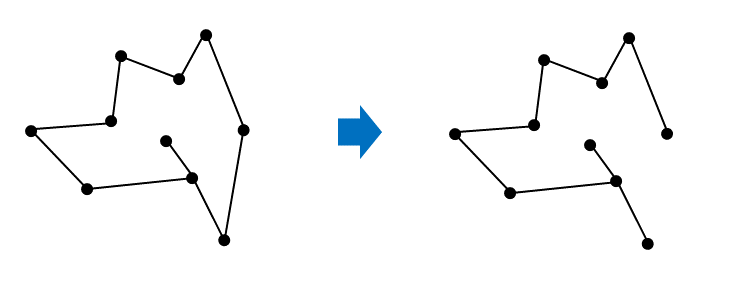
まず（1）についてですが, 仮に, 木が閉路を含んでいる場合を考えると, 閉路上の任意の枝を取り除いても, 依然としてグラフは連結なままです（下図3 参照）. これは木の最小性と反するため, この仮定は成り立たないことが分かります. よって, 木は閉路を含みません.

次に（2）ですが, 連結なグラフにおいて, 全ての節点は既に木に繋がっています. ここで, ある節点A と 節点B の間に新たなリンクを加えた場合を考えてみましょう. 節点A から 節点B に移動しようとするとき, 既に存在していた木を通って移動するパスと, 新たに加えたリンクを通っていくパスの 2つのパスが必ず存在することが分かります. よって, 節点A から木を通って節点B へ行き, 節点B からリンクを通って節点A へ戻ってくることができる, つまり閉路となっていることが分かります.

最後に（3）ですが, これも仮定を用いると自明です. 仮に, 木の枝を 1本取り除いても連結なままだったとすると, 木の最小性に反します.

節点と木の数

グラフが連結であれば, 木の性質から, 木の枝数, 補木の枝数は自然と決定します.

節点を \(n\)個として, 連結なグラフの木の枝数について考えてみましょう.

節点A を節点B に繋げる場合, 枝は 1本です（節点 2個, 枝 1本）. ここでさらに別の節点C と連結するためには, 節点A もしくは 節点B から枝を伸ばして節点C と繋げます（節点 3個, 枝 2本）. 以後同様に, 節点が 1つ増えると, 既に連結されている節点のどれかから枝を 1本伸ばして新たな節点と繋げることで連結となります.

よって, 節点が 1つ増えるごとに, 木の枝が 1本ずつ増えることがご理解頂けると思います. 節点 2つの状態で木の枝は 1本なので, 枝数は節点の数より常に 1 少なくなります.

以上から, 連結なグラフにおける節点を \(n\)個とすると, 木の枝の本数は \(n-1\)$本です.

木以外はすべて補木なので, 全ての枝数を \(b\) とすると, 補木の枝数は \(b-n+1\) となります.

まとめ

以上, グラフの基本性質でした. 冷静に見ていけば, 当り前じゃないかと思われる数字遊びばかりで, 本稿は少々退屈だったかもしれません.

しかし, 前置きでも述べた通り, 閉路方程式やテレゲンの定理など, 回路の重要な概念を理解するためには欠かせない理論です. 今後, これを基本として話を広げていきます. どうぞよろしくお願いします.