テレゲンの定理と多端子対回路における相反定理
前回は閉路方程式の係数行列における対称性を利用して, 相反定理を導出しました.
今回はテレゲンの定理を用いて, 前回導出した相反定理を2端子対回路から多端子対回路へ拡張していきます.
Table of Contents
前回:相反定理(2端子対回路)
まず前回の内容の確認です.
一般に, 閉路電流法を用いると, 閉路電流分布 \(\boldsymbol{I}_{loop}\) と 閉路上に存在する電源の分布 \(\boldsymbol{E}\) に関して, 以下のような閉路方程式が得られます.
\begin{eqnarray} A \boldsymbol{I}_{loop} = \boldsymbol{E} \end{eqnarray}
係数行列\(A\) は対角行列です. そして, \(A\) が対角行列であることから相反定理が導かれます.
ここで言う相反定理とは, 2端子対回路網(端子対を2つ持ち, 内部には電源を持たず, 線形素子のみが含まれる)において,
・端子対1 に電源\(E_a\)を接続し, 端子対2 を短絡させたとき, 端子対2 に流れる電流を\(I_a\)
・端子対2 に電源\(E_b\)を接続し, 端子対1 を短絡させたとき, 端子対1 に流れる電流を\(I_b\)
とすると,
\begin{eqnarray} \frac{I_a}{E_a}=\frac{I_b}{E_b} \;\; \cdots \; (1) \end{eqnarray}
が成り立つ, という定理です.
電気回路以外の分野でも相反定理と呼ばれるものは幾つかありますが, 電気回路の分野で単に「相反定理」と言ったときには, この定理を指すことが多いように感じます.
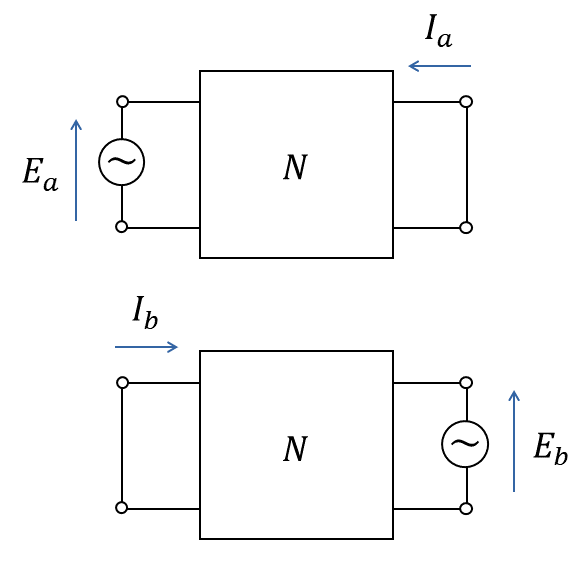
特殊な場合として, \(E_a=E_b\)のとき, \(I_a=I_b\)となり, 「電源」と「電源の反対側の端子対に流れる電流」を左右逆にしたような形になります(下図参照). こちらを相反定理と呼ぶこともあるようです. この性質から, 相反定理は「可逆定理」とも呼ばれます.
相反定理の拡張
式(1)を変形すると, 以下のようになります.
\begin{eqnarray} E_a I_b =E_b I_a \;\; \cdots \; (2) \end{eqnarray}
実は, 電源を接続していない側の端子対を短絡させず, 別の電源を接続した場合についても式(2)のような関係が成り立ちます.
つまり,
・\(N\)に外部回路\(N_a\)を接続し, 各端子対に流れる電流, かかる電圧を\(E_{1a}\), \(I_{1a}\), \(E_{2a}\), \(I_{2a}\)
・\(N\)に外部回路\(N_b\)を接続し, 各端子対に流れる電流, かかる電圧を\(E_{1b}\), \(I_{1b}\), \(E_{2b}\), \(I_{2b}\)
としたとき,
\begin{eqnarray} E_{1a} I_{1b} +E_{2a} I_{2b} =E_{1b} I_{1a} +E_{2b} I_{2a} \;\; \cdots \; (3) \end{eqnarray}
が成り立ちます. 式(3)において, \(E_{1a}=0\), \(E_{2b}=0\) の特殊な場合が式(2)です.
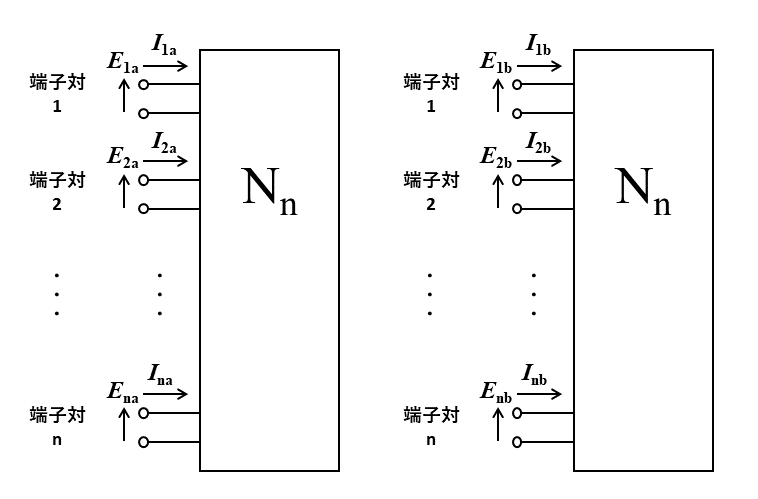
また, これを n端子対回路 \(N_n\) に拡張して,
・\(N_n\)に外部回路\(N_a\)を接続し, 各端子対に流れる電流, かかる電圧を \( ( E_{1a}, I_{1a} ) , \cdots , ( E_{na} , I_{na} ) \)
・\(N_n\)に外部回路\(N_b\)を接続し, 各端子対に流れる電流, かかる電圧を \( ( E_{1b}, I_{1b} ) , \cdots , ( E_{nb} , I_{nb} ) \)
としたとき,
\begin{eqnarray} E_{1a} I_{1b} + \cdots + E_{na} I_{nb} =E_{1b} I_{1a} + \cdots + E_{nb} I_{na} \;\; \cdots \; (4) \end{eqnarray}
も成り立ちます.
相反定理(可逆定理)とは, 「逆にしても同等である」という定理ですが, 式(4)では「取り出す電流と電圧」が左辺と右辺で逆になっています. 各電流電圧の下付き文字を見て頂くと分かりやすいかと.
式(4)の左辺では, \(N_a\)を接続したときの端子対から電圧を, \(N_b\)を接続したときの端子対から電流を取り出して, 各端子毎に積を取っています. 右辺では, 各外部回路を接続したときのに取り出す電圧と電流を逆にします.
式(3) 及び 式(4) はまだ証明していないので, 疑って頂いて大丈夫です. これらを証明することが本稿のテーマとなります.
相反定理
色々な形の相反定理が出てきて, 「相反定理とは何?」というところが曖昧になってきたので, 以下で使うことになる「相反定理」という用語をしっかり定義しておきます.
【相反定理】
線形素子のみからなり, n個の端子対を持つ多端子対回路 \(N\) について,
・外部回路 \(N_A\) を接続したときの各端子対の電圧, 及び電流を \(V_{A1}\), \(\cdots\), \(V_{An}\), 及び \(I_{A1}\), \(\cdots\), \(I_{An}\)
・外部回路 \(N_B\) を接続したときの各端子対の電圧, 及び電流を \(V_{B1}\), \(\cdots\), \(V_{Bn}\), 及び \(I_{B1}\), \(\cdots\), \(I_{Bn}\)
としたとき, 以下を満たす.
\begin{eqnarray} V_{A1} I_{B1} +\cdots +V_{An} I_{Bn} =V_{B1} I_{A1} +\cdots +V_{Bn} I_{An} \end{eqnarray}
書籍によって「相反定理」の定義は異なるように感じます. 各書籍で何を「相反定理」としているのかにご注意ください.
2端子対回路における相反定理が成り立つことは前回の記事で証明しました. 本稿では多端子対回路にも適用できる上記「相反定理」を証明します.
テレゲンの定理
証明にはテレゲンの定理を利用します.
テレゲンの定理とは「各枝で発生する電力を回路全体で足し合わせると, 総和は零」という定理です. 本サイト初出なのでまずはこちらを証明していきましょう.
テレゲンの定理の証明
\(n\)個の節点と \(b\)本の枝を持つ回路を考えます.
枝電圧(枝両端の節点間の電位差)を \(v_{e1}\), \(\cdots\), \(v_{eb}\), 枝電流を \(i_1\), \(\cdots\), \(i_n\), 節点k の電位を \(v_k\)(\(k=1, \ldots , n\))と表記することにしましょう.
枝k が送り出す瞬時電力は \(p_k=v_{ek}i_{k}\) なので, 回路全体では,
\begin{eqnarray} p=\sum_{k=1}^{b} p_k = \boldsymbol{i}^T \boldsymbol{v}_e \;\; \cdots \; (5) \end{eqnarray}
の電力が発生しています. ここで, \(\boldsymbol{i}=[i_1 \cdots i_b ]^T\) , \(\boldsymbol{v}_{e}=[ v_{e1} \cdots v_{eb} ] ^T \) というベクトルで, 各枝における電流と電圧の分布を表しています.
枝電圧と節点電位の関係は, 枝と節点の接続関係そのものであり, 接続行列\(A\)の転置で表すことができます.
\begin{eqnarray} \boldsymbol{v}_e =A^T \boldsymbol{v} \;\; \cdots \; (6) \end{eqnarray}
ここで, \(\boldsymbol{v}=[ v_1 \cdots v_n ]^T\) は, 節点における電位分布を表しています.
これを式(5)に代入して,
\begin{eqnarray} p= \boldsymbol{i}^T A^T \boldsymbol{v} = (A \boldsymbol{i} )^T \boldsymbol{v} \;\; \cdots \; (7) \end{eqnarray}
が得られますが, \(\boldsymbol{i}\) はキルヒホッフの電流則を満たし, \(A \boldsymbol{i}=\boldsymbol{0}\) となるため, 結局, \(p=0\) となります.
よって, 枝電流で生じる電力を回路全体で足し合わせると零となることが分かりました.
テレゲンの定理についてより詳しく
テレゲンの定理は, \(\boldsymbol{i}\) が電流則を満たし, \(\boldsymbol{v}_e\) が電圧則を満たす, ということのみから導かれています.
つまり, 時刻 \(t_1\) における電流分布 \(\boldsymbol{i}(t_1)\) (電流則を満たす)と, 時刻 \(t_2\) における電圧分布 \(\boldsymbol{v}_e(t_2)\) (電圧則を満たす)を用いても成立します.
それどころか, 各枝に含まれる成分には依存していないため, 節点と枝の接続関係が同等である 2つの回路を持ってきて, 一方から電流分布を, 他方から電圧分布を取り出しても成立します.
テレゲンの定理は回路解析やフィルター設計, 故障の検知などに用いられますが, さらに応用して, 化学プラントの設計や生化学的な反応の解析にも広く用いられる重要な定理です.
その意味するところはエネルギーの保存則に似ています. 中学で習う力学的エネルギーの保存則では, 振り子全体としてのエネルギー保存が議論に上がりました. 時刻によって運動エネルギーと位置エネルギーの大きさはそれぞれ異なるものの, それらの和は常に一定となります.
テレゲンの定理も同様です. 交流が印加されているとき, 各枝で生じる電力は時刻によって変化します. しかし, 回路全体で見たときに, その総量は常に一定です.
こうした性質から, テレゲンの定理は「電力保存則」とも呼ばれます.
多端子対回路における相反定理
それでは, 本題である「多端子対回路における相反定理」の証明に移っていきましょう.
証明の方向性
純抵抗のような線形素子に電源を接続して電流を算出し, 続いて別の電源を接続して同様に電流を算出すれば, 相反定理が成立することは簡単に証明できます. つまり, 単端子対回路において相反定理は常に成り立ちます(単端子対回路は相反性を持っている).
また, 線形素子の組み合わせでできている多端子対回路は「線形素子」と「接続のみからなる回路」に分解することができるはずです.
もし仮に, 「線形素子の組み合わせでできる回路でも相反定理が成り立つ」ということが証明できれば, 上記と合わせて, 「あらゆる多端子対回路で相反定理が成り立つ」ということが言えるでしょう.
そこで, 「線形素子の組み合わせでできる回路でも相反定理が成り立つ」ということを以下で証明します.
相反定理(一般)の証明
相反定理を証明したい n端子対回路を \(N\) とし, \(N\) は \(m\)個の線形素子 \(X_1\), \(\cdots\), \(X_m\) で構成されることとします.
このとき, \(N\) は, 「各線形素子」と「接続だけからなる回路 \(N_0\)」に分割できます(図3参照).
続いて, 相反定理を証明するための電源 \(E_{A1}\), \(\cdots\), \(E_{An}\) 及び \(E_{B1}\), \(\cdots\), \(E_{Bn}\) を用意します.
・電源セット \(E_{A1}\), \(\cdots\), \(E_{An}\) を \(N\) の各端子対に接続したとき, 端子対に流れる電流を \(I_{A1}\), \(\cdots\), \(I_{An}\) とし, 各線形素子にかかる電圧, 及び流れる電流を \(V_{XA1}\), \(\cdots\), \(V_{XAm}\), 及び \(I_{XA1}\), \(\cdots\), \(I_{XAm}\)
・電源セット \(E_{B1}\), \(\cdots\), \(E_{Bn}\) を \(N\) の各端子対に接続したとき, 端子対に流れる電流を \(I_{B1}\), \(\cdots\), \(I_{Bn}\) とし, 各線形素子にかかる電圧, 及び流れる電流を \(V_{XB1}\), \(\cdots\), \(V_{XBm}\), 及び \(I_{XB1}\), \(\cdots\), \(I_{XBm}\)
とします.

では, 上記2つの電源セットを接続した状態の回路から, 枝電圧及び枝電流をそれぞれ取り出し, テレゲンの定理を適用してみましょう. 接続のみからなる回路の中には素子が存在せず電圧がかかっていないので, 生じる枝電力は零であり, テレゲンの定理を適用するにあたって考慮する必要はありません.
\begin{eqnarray} &\;& ( E_{A1} I_{B1} + \cdots +E_{An} I_{Bn} )+( V_{XA1} I_{XB1} + \cdots +V_{XAm} I_{XBm} ) \\ &=& ( E_{B1} I_{A1} + \cdots +E_{Bn} I_{An} )+( V_{XB1} I_{XA1} + \cdots +V_{XBm} I_{XAm} ) \;\; \cdots \; (8) \end{eqnarray}
このとき, 各線形素子では相反定理が成り立ちます. 即ち,
\begin{eqnarray} V_{XAk} I_{XBk} =V_{XBk} I_{XAk} \;\; (k=1, \cdots , m) \;\; \cdots \; (9) \end{eqnarray}
式(8)において \(N\)内部の素子にかかる電力の項は式(9)を用いてキャンセルされるため, 結局, 以下のように, \(N\) の各端子対のみに関する式が得られます.
\begin{eqnarray} E_{A1} I_{B1} + \cdots +E_{An} I_{Bn} = E_{B1} I_{A1} + \cdots +E_{Bn} I_{An} \;\; \cdots \; (10) \end{eqnarray}
よって, \(N\) についても相反定理が成り立つことが分かりました.
まとめ
最後までご覧いただきありがとうございました. 本稿の内容を簡単にまとめます.
・テレゲンの定理:各枝で生じる電力を回路全体で足し合わせると零になる.
・テレゲンの定理を使うと, 多端子対回路における相反定理を導出できる.

