アドミタンスはなぜ必要?複素誘電率, モジュラスとの関係
交流回路の基本となる複素インピーダンスは様々に形を変えて用いられます. 代表的なものは「アドミタンス」です.
複素インピーダンスの形を変えることで便利になることも多いですが, そのせいで理解が難しくなることもしばしば.
本稿では, インピーダンスの派生形であるアドミタンスに焦点を当て, アドミタンスとは何か ? なぜアドミタンスを用いるのか ? について話していきます.
また, 後半では同じく複素インピーダンスの派生形である「複素誘電率」「モジュラス」との関係に触れます.
Table of Contents
インピーダンスとアドミタンス
インピーダンスとは
複素インピーダンス \( \dot{Z} \) とは直流回路の「抵抗」に対応する概念であり, とある交流回路の両端にかかる電圧 \( \dot{V} \) と流れる電流 \( \dot{I} \) の関係を表すものです. 単位は \( \left[ \Omega \right] \).
$$ \dot{Z} = \dot{V} / \dot{I} $$
交流回路でフェーザ表示(複素数表示)した電圧を, 同じくフェーザ表示した電流で割ったものなので, 複素インピーダンスは複素数です.
また, 周波数に依存するという特徴を有します. つまり回路に印加する電圧の周波数を変化させることで複素インピーダンスの値も変化するということです.
複素インピーダンスを図として表示する方法は主に2つありまして, 周波数を横軸にとったものが Bode plot, 横軸に複素インピーダンス実部, 縦軸に虚部を取ったものが Cole-Cole plot です.
複素インピーダンスの表示:Cole-Cole plot と Bode plot
アドミタンスとは
アドミタンス(Admittance)\( \dot{Y} \) とは「複素インピーダンス」の逆数です.
$$ \dot{Y} = \dot{Z}^{-1} = \dot{I} / \dot{V} $$
単位はジーメンス \( \left[ S \right] = \left[ \Omega ^{-1} \right] \) が用いられます.
複素インピーダンスの逆数を取っただけなので, 実質, アドミタンスと複素インピーダンスは全く同じものを表していて, アドミタンスにできることは複素インピーダンスにもすべてできます.

アドミタンスを用いる利点
アドミタンスにできることは複素インピーダンスにもすべてできる, ならばアドミタンスの存在意義とは何なのでしょうか ?
並列回路の計算が楽
アドミタンスの存在意義1つ目は「並列回路の計算が楽になること」です.
試しに 抵抗 \( R \) と キャパシタ \( C \) の並列回路について, 複素インピーダンスとアドミタンス双方の実部と虚部を求めてみます.
以下で, \( j \) は虚数単位, \( \omega \) は角周波数 です.
・複素インピーダンス
\begin{eqnarray} \dot{Z} &=& \left( R^{-1} + j \omega C \right) ^{-1} \\ \rm{ } \\ &=& \left( \frac{1 + j \omega CR}{R} \right) ^{-1} \\ \rm{ } \\ &=& \frac{R}{1 + j \omega CR} = \frac{R \, (1 – j \omega CR)}{1 + \omega ^2 C ^2 R ^2} \\ \rm{ } \\ \mathrm{Re} \, (\dot{Z}) &=& \frac{R}{1 + \omega ^2 C^2 R^2} \\ \rm{ } \\ \mathrm{Im} \, (\dot{Z}) &=& \frac{- \omega CR}{1 + \omega ^2 C^2 R^2} \end{eqnarray}
・アドミタンス
\begin{eqnarray} \dot{Y} &=& R^{-1} + j \omega C \\ \rm{ } \\ \mathrm{Re} \, (\dot{Y}) &=& R^{-1} \\ \rm{ } \\ \mathrm{Im} \, (\dot{Y}) &=& \omega C \end{eqnarray}
お分かりいただけたでしょうか, いかにアドミタンスの計算が簡単か.
アドミタンスは並列に多数の線形素子が接続されているときに本領を発揮します. 逆に直列に接続されているときには, 複素インピーダンスを使った方が計算が簡単です.
物理的に意味のある定数と対応させる
アドミタンスの存在意義2つ目は「実部と虚部を物理的に意味ある定数に対応させられること」です.
これだけでピンとくる方は稀ですので, 誘電体の電気物性を例に説明を試みます.
誘電体は導電性をほとんど示さず直流電流に対しては絶縁体として振舞いますが, 印加される電界に応じて電気的な分極が生じる物体のことです.
分極とは誘電体内部に存在する電気双極子が特定の向きに整列する現象を指します. 高校でフワッと習いました.
誘電体はコンデンサや半導体素子のゲート絶縁膜, 光ファイバーなど様々に応用される重要な電気材料です.
誘電体については20世紀に精力的な研究の結果, その電気特性も定式化され, 誘電体を「抵抗 \( R \) と キャパシタ \( C \) の並列回路」で表現できることが知られています.
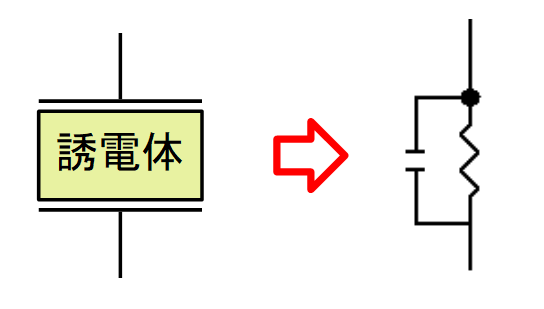
誘電体がこのように表されるのは, 「デバイ緩和」という誘電分極モデルの帰結です. デバイ緩和モデルは液体や高分子の誘電体において実験結果との良い一致が知られています.
参照 : Cole, Kenneth S, Robert H, “Dispersion and Absorption in Dielectrics: I – Alternating Current Characteristics”. Journal of Chemical Physics. 9 (4) (1941).
さて, この RC並列回路のアドミタンスの実部, 虚部は前章で述べた通り,
\begin{eqnarray} \mathrm{Re} \, (\dot{Y}) &=& R^{-1} \\ \rm{ } \\ \mathrm{Im} \, (\dot{Y}) &=& \omega C \end{eqnarray}
となり, 実部が「抵抗のアドミタンスの大きさ」, 虚部が「キャパシタのアドミタンスの大きさ」をそれぞれ表しています. 一方, 複素インピーダンスの実部と虚部は,
\begin{eqnarray} \mathrm{Re} \, (\dot{Z}) &=& \frac{R}{1 + \omega ^2 C^2 R^2} \\ \rm{ } \\ \mathrm{Im} \, (\dot{Z}) &=& \frac{- \omega CR}{1 + \omega ^2 C^2 R^2} \end{eqnarray}
となり, 実部と虚部は意味ある物理量を表していません.
誘電体においてはインピーダンスで電気物性を表現するよりも, アドミタンスで表現する方が誘電体に関する物理量の議論が容易になります.
同様に, RL直列回路を考える場合には, 複素インピーダンスの実部と虚部は,
\begin{eqnarray} \mathrm{Re} \, (\dot{Z}) &=& R \\ \rm{ } \\ \mathrm{Im} \, (\dot{Z}) &=& \omega L \end{eqnarray}
となりますが, アドミタンスの実部と虚部は
\begin{eqnarray} \mathrm{Re} \, (\dot{Y}) &=& \frac{R}{R^2 + \omega ^2 L^2} \\ \rm{ } \\ \mathrm{Im} \, (\dot{Y}) &=& \frac{- \omega L}{R^2 + \omega ^2 L^2 } \end{eqnarray}
となり, アドミタンスの実部と虚部に意味はありません.
対象とする回路の形に応じて複素インピーダンスとアドミタンスを使い分けることで, 実部と虚部を意味ある物理量と対応させることができるのです.

アドミタンス以外の派生形
回路の形に応じて「複素インピーダンス」と「アドミタンス」を使い分けると実部と虚部を物理量と対応させやすくなり, 回路の解析が容易になります.
複素インピーダンスの派生形は「アドミタンス」だけではありません. 複素インピーダンスは回路の形や扱う物理量に応じて形を変えて用いられます.
複素誘電率
先述の「デバイ緩和」のオリジナルの論文では, 複素インピーダンスの代わりに「複素誘電率」が用いられます. 誘電体の電子物性を扱う分野では複素誘電率を用いることが一般的です.
複素誘電率 \( \varepsilon \) と複素インピーダンス \( \dot{Z} \) の関係は以下のように表せます.
$$ \varepsilon = \frac{1}{j \omega \dot{Z}} \, \times \, \frac{L}{S} $$
ここで, \( L \) は試料の長さ(厚み), \( S \) は試料の断面積で, 一般に複素誘電率の単位はファラッド毎メートル \( \left[ \mathrm{F/m} \right] \) です.
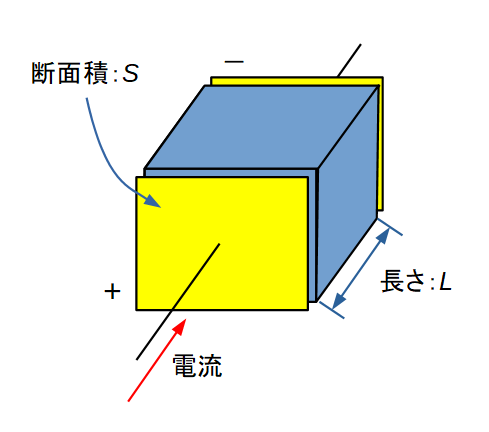
複素インピーダンスに掛けられている数は「角周波数」や「試料の長さ」など, 物質に固有でない物理量なので「複素インピーダンス」と「複素誘電率」が本質的には同じものを表している, ということが分かります.
高校で習った「誘電率」とはこの複素誘電率の実部を指します.
実際に, 純粋なキャパシタのインピーダンスから, 上式を使って複素誘電率を算出してみます.
キャパシタの複素インピーダンスは \( \left( j \omega C \right) ^{-1} \) なので,
$$ \varepsilon = \frac{j \omega C}{j \omega} \, \times \, \frac{L}{S} = C \, \frac{L}{S} $$
となり, 高校で習った誘電率と同じものであることが分かります.
また, 複素誘電率の虚部を「誘電損失」と呼び,
「( 複素誘電率の虚部 / 複素誘電率の実部 ) \( \, \times \, (-1) \)」を「誘電正接」と呼びます.
この辺りについては誘電体を扱うときに詳しく解説します. 例の如くいつになるかは分かりませんが.
モジュラス
最後はモジュラス(modulus)です.
モジュラス \( \dot{M} \) は以下のように表されます.
$$ \dot{M} = j \omega \dot{Z} $$
それはつまりこういうことでもあります.
$$ \varepsilon = \frac{1}{\dot{M}} \, \times \, \frac{L}{S} $$
複素誘電率とはモジュラスの逆数を単位体積で規格化した物理量なのです.
Google検索すれば分かる通り, modulus という物理量はかなりマイナーな物理量であり, 覚えていても役に立つことはまずないでしょう.
しかし, モジュラスがインピーダンスより優れている点が1つだけあります. それは「Cole-Cole plot 上の円弧の大きさが高周波側ほど大きく見える」ことです.
電池の電気化学測定によって得られる複素インピーダンスの Cole-Cole plot は大抵の場合, 高周波側の円弧が小さすぎて潰れてしまいます.
しかし, これをモジュラスによって表示することで下図の通り, 円弧が潰れず, 解析が容易です.
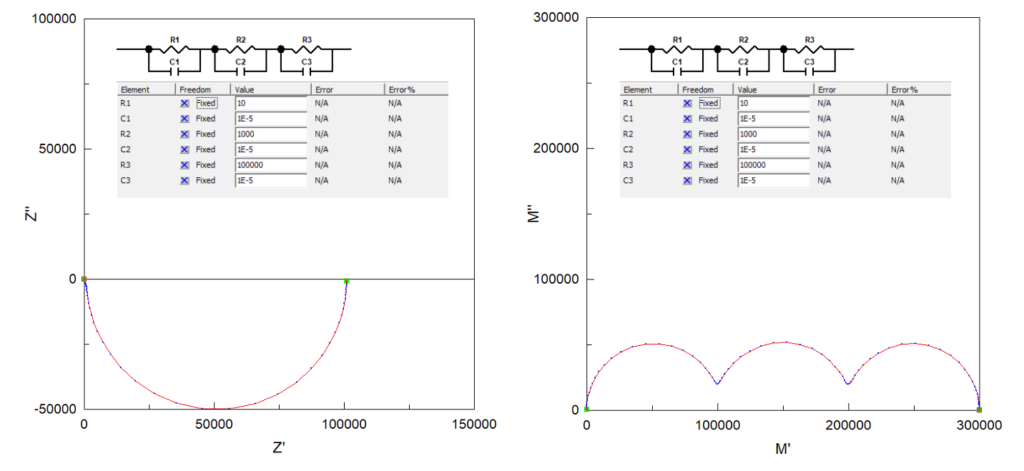
測定結果を複素インピーダンスの Cole-Cole plot のみで眺めるのではなく, アドミタンスやモジュラスを使ったり, Bode plot を使ったり, はたまた両対数表示してみることで現象を理解しやすくなったり, 理解しにくくなったりします.
まとめ
最後に, 複素インピーダンス, アドミタンス, 複素誘電率, モジュラスについて表にまとめます.

こういうものを見ると「ややかしいから統一した方が良いのでは」と感じざるを得ませんが, 歴史的な背景や分野ごとの力関係がありますので一筋縄とはいきません.
今回の話の中で一番大事なことは「結局全部同じ」ということです.
現象を複素誘電率で表しても, 複素インピーダンスで表しても, 見ているものが変わるわけではありません. しかし, 別の角度から見ることで, 見やすくなったり, 見にくくなったりします.
複素誘電率って何だっけ ? とか, アドミタンスって何だっけ ? と思ったときにはまた見に来て下さると嬉しい限りです.

