キルヒホッフの法則と基本カットセット行列
キルヒホッフの電流則(KCL)と電圧則(KVL)は回路解析の基本となる法則です. 直観的にも理解しやすい法則ですが, グラフを交えて見つめ直すとより理解が深まることでしょう.
本稿では, キルヒホッフの電流則に深く関係する「カットセット」という考え方を導入し, KCL の系統的な立式を目指します.
Table of Contents
KCL と KVL を無駄なく系統的に
今回はキルヒホッフの法則を扱いますが, まずは, それらの辞書的な定義をおさらいします.
◆ キルヒホッフの第1法則(電流則, Kirchhoff’s Current Low, KCL)
「回路中の任意の接続点に流入する電流の和は零である」
◆ キルヒホッフの第2法則(電圧則, Kirchhoff’s Voltage Low, KVL)
「回路中の任意の閉路を一巡するとき, 起電力の総和と電圧降下の総和は等しい」
どちらの法則についても, そうならない場合を仮定すると自明であることがよく分かります.
仮に, KCL が成立せず, とある接続点で流入する電流の和が零でないとします. すると, その接続点では継続的に電子が生成されたり, 消失したりしていることになります. これはおかしい.
また, KVL が成立しない場合, つまり一周して元の電位に戻らない場合, 何周もすれば無限に電位が下がっていったり, 上がっていったりすることになります. これも明らかにおかしい.
以上のように, KCL と KVL は, 直観的に理解しやすい法則です. これ以上何を議論することがあるのかと思うかもしれません. 以下では, 高校で議論し尽くせなかった領域に触れていきます.
問題提起:1次独立な式の数
本稿で議論したいこととは, 「1次独立な KCL と KVL の数」についてです.
例として, 下図1 をご覧ください.
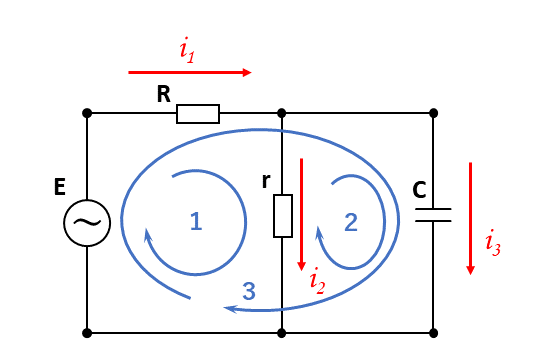
図1中の閉路1, 閉路2, 閉路3 ではそれぞれ KVL を使って立式することができます. それが以下の式です.
\begin{eqnarray} \begin{array}{lll} \; \; &{閉路1}& \; &{\rm :}& E -Ri_1 -ri_3 = 0 \; &{\cdots}& \; (1-1) \\ \; &{閉路2}& \; &{\rm :}& ri_3 -(j \omega C)^{-1} \: i_2 = 0 \; &{\cdots}& \; (1-2) \\ \; &{閉路3}& \; &{\rm :}& E -Ri_1 -(j \omega C)^{-1} \; i_2 = 0 \; &{\cdots}& \; (1-3) \end{array} \end{eqnarray}
式が 3つできましたが, この 3つの式は 1次独立(※1)ではありません. 実際, 式1-1 と 式1-2 を辺々足すことで, 式1-3 を導出することができます.
よって, 図1 の回路において, 1次独立な KVL の式の数は 『2』 です.
KVL の作り方については, 中学(または高校)で以下のように習った人もいるでしょう.
曰く, 「重ならないように, 全部の場所を通ればいい」と.
つまり, 図1 の閉路1, 閉路2 で既に KVL を立式した後, 閉路3 を加える場合, 閉路3 が通る全ての道は, 既に閉路1, 閉路2 で通っている. よって, 閉路3 による KVL は 1次独立な組に加えられないのだ, ということです.
また, 閉路1 だけでは回路の右側の部分を通っていません. よって, 1次独立な全ての式を作れていないことになります.
上記のような方針でも, 多くの場合問題は起きません. しかし, 複雑な回路の解析をする場合などには問題となってきます. 一般的な立式方法を知っておくに越したことはありません.
では今度は KCL について考えてみます. 図1 において 1次独立な KCL の式はいくつあるでしょうか?
答えから言えば, それは 『1』 です.
実際に KCL を立ててみれば分かりますが, 節点1 と節点2 で立てられる KCL は, 正負が逆なだけで, 全く同じ形をしています.
しかし, 高校までの数学(物理?)では, 「なぜ 1次独立な KCL は 1つだけしかないのか?」という疑問に答えることはできません.
改めて振り返ってみれば, KCL と KVL については, 中学高校でざっくりとしか学んでいないことが分かります. 「どんな場合にも通用する, 系統的な立式アルゴリズム」を学んでいないのです.
本稿で扱いたいのは, 上記のような「式の立て方」です. 「無駄なく系統的に」キルヒホッフの法則を立式するためにはどうすればよいか, ということについて, グラフと絡めて扱って参ります.
また, KCL や KVL をグラフ(つまり行列)で扱う方法を理解すると, 今後やる予定の「テレゲンの法則」や, 「相反定理」を理解しやすくなります. どちらかと言えば, こちらの方がメインかもしれません. 何にしても回路を系統的に扱うときに基本となる内容です.
(※1)1次独立:ある式(ベクトル)を, 他の式の線形結合で表せること.
KCL の拡張
前置きが長くて申し訳ないのですが, 本筋の話をする前に, 1つだけ準備をしておきたいと思います. その準備とは「KCL の拡張」です.
KCL とは, 「とある点に流入する電流の総和は零」を意味しますが, これは特段「点」に限ったことではありません. 「領域」に拡張しても良いのです. 勘の良い方はこれだけで意味が分かるかもしれませんが, 普通はそうではないはずです. 以下で詳しく解説します.
電流は電子という粒子の流れです. 川(回路)を流れるとき, 水車(抵抗)で勢いを減じられたり, ポンプ(電源)で勢いを増すことはありますが, どこかに流出(放電)しない限り, 水量(電子の数)自体は変わりません.
とある川に, 10 m の区間A を設け, 単位時間に区間A に入り込む水の量と, 出ていく水の量を比べれば(雨が降らない限り)当然両者は等しいはずです.
同じことが電気回路でも言えます.
例えば, 下図のように, ある領域B を設け, そこに流入する電流を考えれば, KCL は成立します.
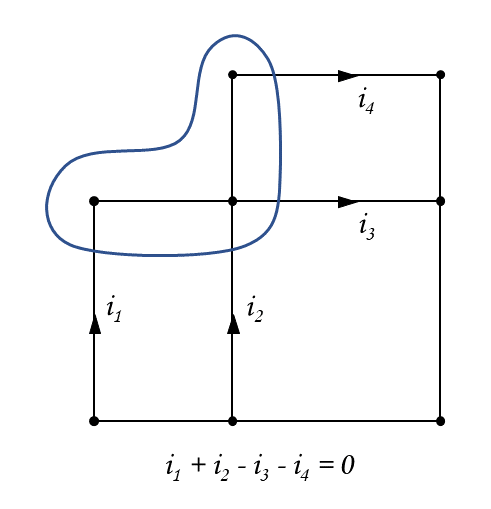
また, 「回路中のとある接続点P に流入する電流の和」は, 「回路中の P 以外のすべての領域から流出する電流の和」と言い換えることもできます.
言われてみれば当たり前かもしれませんが, 押さえておいて欲しい重要な事実です. これは, 次に説明する「カットセット」という考え方と大きく関係してきます.
カットセットとは
ここからやっと本題です. グラフの話をします.
後で KCL の話と繋がってきますので, 繋がりが分かるまで苦痛かもしれませんが, ご容赦下さい.
とある連結グラフ \(G\) を考えます. グラフとは, 節点と枝の集合のことでした. つまり, \(G\) とは「節点の集合」と「枝の集合」を合わせたものです.
この \(G\) の中の「節点」を \(U\) と \(V\) という 2つの集合に分けます.
すると \(G\) に含まれる枝は, 「\(U\) の中の節点同士を繋ぐ枝集合 \(A\)」, 「\(V\) の中の節点同士を繋ぐ枝集合 \(B\)」, 「\(U\) の節点と \(V\) の節点とを繋ぐ枝集合 \(C\)」の 3つのグループに分けられるはずです.
この最後に登場した枝集合 \(C\) を「カットセット」と呼びます.
カットセットを \(G\) から取り除くと, \(G\) は連結ではなくなり, 2つの連結グラフに分かれます. つまり, カットセットとは 1つの連結グラフを 2つの連結グラフに分割(Cut)する枝集合(Set)なのです.
また, カットセットを取り除いた後, カットセットの中の枝を 1本でも \(G\) に戻すと, \(G\) は再び連結となる, という性質を持っています.

基本カットセット行列
カットセットには様々な作り方があります. 1つの節点に繋がった枝の集合はカットセットの代表例です.
また, 木の性質(※2)から, 「木の枝 1本と残りはリンクからなるカットセット」を作ることができるはずです. このようなカットセットは木の本数(即ち, 節点の数 -1)だけあります.
この「木の枝を 1本だけ含むカットセット」の集合を「基本カットセット系」と呼びます.
下図を例として, 基本カットセット系を行列で表してみましょう.
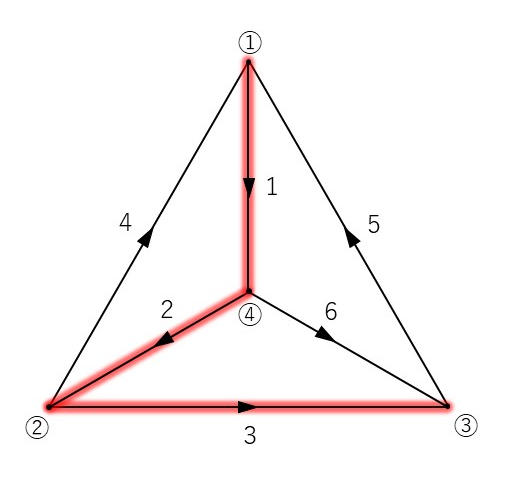
図4 回路の例(赤い枝は木枝, その他の枝はリンク)
ここでは, 木の枝に若い番号を付し, リンクの番号は木の枝の番号より大きく設定しています. すると, 図4 のグラフについての基本カットセット行列が以下の式2 のように表されます.
\begin{eqnarray} C = \left[ \begin{array}{rrr} 1 & 0 & 0 & -1 & -1 & 0 \\ 0 & 1 & 0 & -1 & -1 & 1 \\ 0 & 0 & 1 & 0 & -1 & 1 \end{array} \right] \; \cdots \; (2) \end{eqnarray}
この行列が意味するのは, 各カットセット(行)に各枝(列)がどのように含まれているのか, ということです. 第1行は枝1 を含むカットセット, 第2行は枝2 を含むカットセット, 第3行は枝3 を含むカットセットをそれぞれ表します. 各カットセットに対応する枝が含まれていれば 1, そうでない場合は 0 が記されます.
カットセットは「1つの連結グラフを2つの連結グラフに分割する枝集合」でした. 例えば, 枝1 を含むカットセットは節点1 を他の節点から切り離します. このとき, 枝1 は「節点1 からなるグラフ」側に始点を持ち, 「節点1以外からなるグラフ」側に終点を持っています. 1行目ではこれを正の方向としています.
この正の方向と各枝の向きが同じ場合は正(1), 逆向きの場合は負(-1)が記されています.
注目して欲しいのは, 基本カットセット行列 \(C\) の左側が, 単位行列になっている, ということです.
今回は木の枝から先に番号を付して, 左側に寄せています(リンクには大きな番号を付して, 右側に寄せました). 加えて, 木の枝はそれぞれのカットセットに 1本ずつしか含まれていません. 故に \(C\) の左側に単位行列ができるのです.
(※2)前回記事参照
KCL と基本カットセット行列
KCL と基本カットセット行列には深い関係があります. その関係(下記の式3)こそ, 本稿中で最もお伝えしたいことです. 初めて学ぶ方は, なぜそうなるのか分からないと思いますが, 後で詳しく解説するので落ち着いて読み進めてください.
基本カットセット行列 \(C\) と, 電流ベクトル \( \boldsymbol{i} \) からなる以下の式
\begin{eqnarray} C \boldsymbol{i}= \boldsymbol{0} \; \cdots \; (3) \end{eqnarray}
は, 1次独立な全ての KCL を表す.
これがどういうことか, 具体的に見ていきましょう.
図4 を例にとると, 式3 とはつまりこういうことです.
\begin{eqnarray} \begin{array}{lll} \; &{カットセット1}& \, &{\rm :}& i_1 -i_4 -i_5 = 0 \; &{\cdots}& \; (4-1) \\ \; &{カットセット2}& \, &{\rm :}& i_2 -i_4 -i_5 +i_6 = 0 \; &{\cdots}& \; (4-2) \\ \; &{カットセット3}& \, &{\rm :}& i_3 -i_5 +i_6 = 0 \; &{\cdots}& \; (4-3) \end{array} \end{eqnarray}
この 1番上の式について考えてみます.
\begin{eqnarray} i_1 -i_4 -i_5 = 0 \; \cdots \; (4-1) \end{eqnarray}
枝集合(1, 4, 5)は, 枝1 を含む基本カットセットです. グラフを節点1 と, それ以外の部分に分割するカットセットでもあります.
よって, \(i_1 -i_4 -i_5\) は「節点1 に流入する電流の和」を表しています. これが「零になる」ということが示すのは, まさしく KCL です. つまり, 式4-1 は, 「節点1 に関する KCL」なのです.
他の式も意味するところは同様ですが, 上から 2番目の式は少々様子が異なります.
\begin{eqnarray} i_2 -i_4 -i_5 +i_6 = 0 \; \cdots \; (4-2) \end{eqnarray}
式4-2 は 枝2 を含むカットセットです. グラフを節点集合(1, 4)と, 節点集合(2, 3)に分割するカットセットでもあります.
ここで, 「拡張した KCL」という考え方を思い出して下さい. この式4-2 のカットセットが表しているのは, まさに「拡張した KCL」だということがお分かり頂けるでしょうか?
これは「節点集合(1, 4)からなる領域に流入する電流の和が零」ということを表しています. 「節点集合(2, 3)からなる領域(残りの領域)から流出する電流の和が零」と言い換えても同じことです.
節点ではなく, カットセットを使うことで, 「とある領域に流入する電流の和が零」 = 「拡張した KCL」を考えることができるようになったわけです.
カットセットが KCL と大変密接に関係していることをご理解頂けたでしょうか?
では次に, 式3 で与えられる KCL のセットは本当に 1次独立なのか, について考えます.
しかし, これは自明です. 「1次独立であること」は行列の中身を見ればすぐに分かります. 例えば, 式4-1 は枝1 の電流を含みますが, その他の式に枝1 の電流は含まれません. よって, その他の式の線形結合で式4-1 を作ることはできません. これは他の式についても同じことが言えます. よって, 上記 KCL セットは 1次独立です.
最後に, 「全ての KCL を表しているのか」について考えてみます. これは, 逆に言えば「1次独立な KCL はこれ以外にない」ということです. また, 「他の KCL を立式したとしても, その KCL は, 既存の KCL に対して 1次独立でない」と言い換えることもできます.
これは自明ではありません.
「これ以外に KCL が無いのか」については詳しく考える必要があるでしょう.
基本カットセット行列は全ての KCL を表しているのか?
以下では \(C {\boldsymbol i} = {\boldsymbol 0}\) が 1次独立な「全ての KCL」を表していることを証明します.
しかし, これを示すためには, 代数やら群論やらについての知識が必要です. 厳密な証明については他サイト様にお任せし(※3), ここでは, 視覚的に分かりやすい, 直観的な説明に留めます.
それで分かった気になって頂ければよし. そうでなければ, リンク先の詳細な説明をご覧下さい.
まず, 状況を整理します.
1次独立な KCL を木の枝の数(節点の数 -1)と同じだけ作る方法は上で示しました. \(C {\boldsymbol i} = {\boldsymbol 0}\) は 1次独立です.
また, 節点の数より多く KCL を作ろうとすれば, 1次独立でなくなってしまうことは自明とさせて頂きたいと思います.
つまり, 節点それぞれについて KCL を立てた後, 他の KCL を立てようとすれば, 節点(1, 2)からなる領域, などの拡張した KCL で式を立てるしかありません. しかし, これは明らかに 節点1 についての KCL と, 節点2 についての KCL の線形結合になっています.
以上のことから, 1次独立な KCL の数は「節点の数と等しい」もしくは「節点の数 -1」のどちらかです. 後は, 「節点の数と等しい」を否定できれば, 「節点の数 -1」, つまり, 木の枝の数と等しいことが示せます.
状況整理はここまで. 以下では, 「各節点での KCL の式の組」について考え, これが 1次独立でないことを示します.
まず, 節点が \(n\)個だとすれば, 各節点に対応した KCL の式の数も \(n\)個です.
ここで思い出して頂きたいのは, 「分割された 2つの連結グラフについて, 片方の連結グラフに流入する電流の和を考えることと, もう片方の連結グラフから流出する電流の和を考えることとは同じ意味」だということです.
極端な例で言えば, 「A という人間が森羅万象に対して与える影響を考えることと, 森羅万象が A から受ける影響を考えること」とは同じことを意味します.
回路に戻って考えます. 「節点n についての KCL」は, 「節点(1, 2, \(\cdots\), n-1)からなる領域についての拡張した KCL」と同じです. そして, 後者は, 節点1, 2, \(\cdots\), n-1 についての線形結合で表せます. よって, 節点1, 2, \(\cdots\), n-1 についての KCL を既に持っている場合, 節点n についての KCL は, 1次独立ではありません.
以上から, 1次独立な KCL は, 木の枝の数(節点の数 -1)だけあることが分かります. \(C {\boldsymbol i} = {\boldsymbol 0}\) は 1次独立な『全ての』 KCL を表しているのです.
(※3)グラフの理論(東京大学工学部計数工学科, 『経営科学』第9巻1号, 1965)
KVL と基本閉路行列
最後に KVL についても触れておきますが, KCL とグラフの関係が分かれば, KVL も同じように考えることができます.
「木の枝」と「カットセット」と「KCL」に深い関係があることは上で述べた通りです. 同じように, 「リンク」と「閉路」と「KVL」にも密接な関係があります.
こちらはカットセットよりも直観的に理解しやすいでしょう.
「木の枝の数」 = 「基本カットセットの数」 = 「1次独立な KCL の数」であったように,
「リンクの数」 = 「基本閉路の数」 = 「1次独立な KVL の数」です.
基本閉路という言葉を定義していないので, 以下で詳しく説明します.
まず, リンクが 1本もないグラフには, 閉路は 1つもありません. これはグラフの基本性質です.
また, グラフにリンクを 1本追加すると, 「1本のリンクと, 残りは木の枝からなる閉路」が 1つできます. これを「基本閉路」と呼ぶことにします. リンクが 2本なら基本閉路は 2つ. リンクが 3本なら, 基本閉路は 3つです. リンクの数と基本閉路の数は一致しています.
以下では具体例で考えていきましょう.
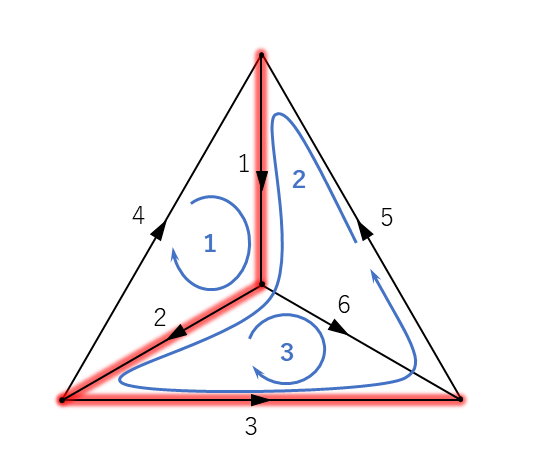
図4′ のグラフについて「基本閉路に含まれる枝」を表す行列を作りましょう. 基本閉路に回転の向きを定義し, 閉路に含まれる枝の方向を考慮して, 各枝における起電力(電圧降下)を書き表すと以下となります.
\begin{eqnarray} B = \left[ \begin{array}{rrr} 1 & 1 & 0 & 1 & 0 & 0 \\ -1 & 1 & 1 & 0 & 1 & 0 \\ 0 & 1 & -1 & 0 & 0 & 1 \end{array} \right] \; \cdots \; (5) \end{eqnarray}
この \(B\) を基本閉路行列と呼びます. 基本閉路行列の行数は, 当然, リンクの数と一致します.
基本カットセット行列と同様, 基本閉路行列も特殊な構造を持っています.
基本閉路行列の右側はリンクの含まれ方を表しており, 各基本閉路にリンクは 1本ずつ含まれているので, 行列の右側が単位行列となっているのです. このことから, 基本閉路行列が 1次独立であることが分かります. 左側の行列が表すものは「木の枝の含まれ方」です.
基本カットセット行列 \(C\) と電流ベクトル \({\boldsymbol i}\) で KCL を表せるように, 基本閉路行列 \(B\) と 電圧ベクトル \({\boldsymbol v}\) を使って表される以下の式
\begin{eqnarray} B {\boldsymbol v} = {\boldsymbol 0} \end{eqnarray}
は, 1次独立な全ての KVL を表します.
KCL の場合と異なり, 1次独立な KVL がこれ以外にないことは明らかでしょう. これ以外の閉路を考えた場合には, 基本閉路の線形結合による閉路しかあり得ないからです.
まとめ
以上, KCL と KVL についてでした.
基本カットセット行列とは何なのか, という点について, ネット上の記事では何となく分かりにくかったため, 自分が分かりやすいと思う語り方に変更しました.
分かりやすさを意識したために冗長になってしまったかもしれませんが, 最後まで読んでくださった方, ありがとうございます.