閉路電流法は大変便利な回路解析手法ですが, 高校までの物理では「なぜこのような解析方法が許されるのか？」についての議論をしてきませんでした.
本稿では, 閉路電流法の根拠となる式を導出し, 気持ちよく閉路電流法を使えるようになること, そして, 閉路電流法に関する理解を深めることを目指します.
目次
閉路電流法
まず, 閉路電流法とは何だったのか, 具体例と共におさらいしましょう.
閉路電流法とは？
閉路電流法は, 各枝に流れる電流を「閉路電流」という仮想の電流で置き換える回路解析方法で, 閉路が複数ある場合に有効な方法です.
閉路電流法は以下のような手順で実行します.
- 閉路電流という未知電流を設定し, 枝電流を閉路電流で置き換える.
- 各閉路で KVL（キルヒホッフの電圧則）を使って式を立てる.
- KVL を連立させて解く.
閉路電流の数（つまり, 未知数の数）と KVL の数（つまり, 式の数）は同じなので, この連立方程式は解が 1つに定まります.
以下で例を挙げて, もう少し詳細に解説します.
閉路電流法の例題
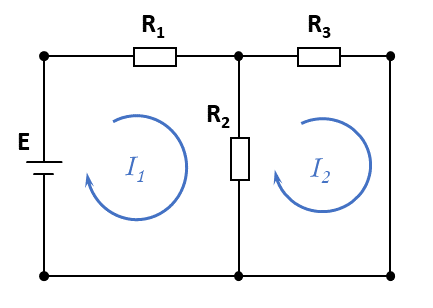
図1 の回路において, 各枝を流れる電流を求めてみましょう. ここで, $I_1$, $I_2$ が閉路電流です.
$I_1$, $I_2$ を図1 のように設定すると, 抵抗 R1 を流れる電流は $I_1$, 抵抗 R2 を流れる電流は $I_1-I_2$, 抵抗 R3 を流れる電流は $I_2$ となります.
閉路電流を使って KVL の式を立てたものが以下の式です.
\begin{eqnarray} \begin{array} \; E-R_1I_1-R_2(I_1-I_2) &=& 0 \;\;\;\;\;\; (1-1) \\ \; -R_2(I_2-I_1)-R_3I_2 &=& 0 \;\;\;\;\;\; (1-2) \end{array} \end{eqnarray}
これを解くと, $I_1=(R_1+R_3)E{R_a}^{-1}$, $I_2=R_2E{R_a}^{-1}$ $(R_a=R_1R_2+R_2R_3+R_3R_1)$となります. R1, R3 を流れる電流はそれぞれ $I_1$, $I_2$となり, R2 を流れる電流は $I_1-I_2=(R_1-R_2+R_3)E{R_a}^{-1}$ です.
問題提起：枝電流と閉路電流の関係
閉路電流は「仮想的な電流」であるということを, ここで再度述べさせていただきます.
閉路に独立した閉路電流が還流しているわけではなく, 実際にはそれぞれの枝を流れる電流が存在するに過ぎません. こうすれば解析が楽になる, という理由で閉路電流を設定したのです.
図1 を再度ご覧ください. KVL を連立させて導出した閉路電流 $I_1$ と 抵抗 R1 を実際に流れる電流が同じだと考えていますが, 本当にそうでしょうか？
仮想的に設定した閉路電流と枝電流は本来別のものです. この2つがが同じものだ, という命題の答えは自明ではありません. どのような電流分布でも, 閉路電流で置き換えてよいものなのでしょうか？
そもそも, 「閉路電流」とは何なのでしょう？閉路を流れる仮想的な電流ですが, 高校範囲では数学的に定義していません.
高校までの物理の授業では, 上述した自明でない事柄を華麗にスルーし, 数学的な根拠を与えませんでした. 閉路電流法を習ったほぼ全ての人が, いつのまにか図1 の抵抗 R1 に流れる電流が閉路電流 $I_1$ と同じものだと思ってしまっているのです.
もちろん, 回路の解析法は実用的な技術であって, その根拠となる数学は絶対に必要というわけではないでしょう. 実際, 閉路電流 $I_1$ と 抵抗 R1 を流れる電流は同じものですし, これで十分実用に堪えます.
しかし, この問題を解消することで閉路電流法に対する理解は深まるはずです. 何より, 気持ちよく閉路電流法を使うことができるようになるでしょう.
色々言いましたが, つまり気持ちいいんだよ. ちょっとやってみようぜ！（※1）
（※1）寿司 虚空編
準備：行列 ABC
これより, 閉路電流法の根拠となる式を導出していきますが, そのために準備が必要となります.
過去2回の記事で, 接続行列 $A$, 基本閉路行列 $B$, 基本カットセット行列 $C$ を扱いましたが, 今回はこれら行列の中身が重要になってきます. これまでさらっと触れてきた各行列の性質を詳しく見ていきましょう.
各行列の意味するもの
接続行列 $A$, 基本閉路行列 $B$, 基本カットセット行列 $C$ はそれぞれ次のような意味を持つ行列でした.
接続行列 $A$：節点と枝の接続関係. 行が節点, 列が枝を表す.
基本閉路行列 $B$：基本閉路に対する各枝の含有関係. 行が閉路, 列が枝を表す.
基本カットセット行列 $C$：基本カットセットに対する各枝の含有関係. 行がカットセット, 列が枝を表す.
図2 を例として, 接続行列 $A$, 基本閉路行列 $B$ と, 基本カットセット行列 $C$ をそれぞれ表してみましょう.
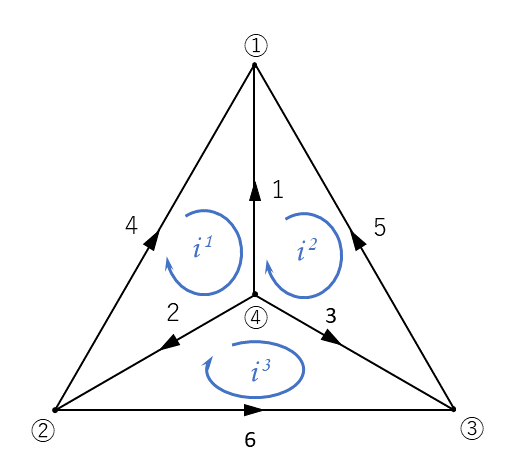
\begin{eqnarray} A &=& \left[ \begin{array}{rrrr} 1&0&0&1&-1&0 \\ 0&1&0&-1&0&1 \\ 0&0&1&0&1&-1 \\ -1&-1&-1&0&0&0 \end{array} \right] \;\;\;\;\;\; (2) \\ B &=& \left[ \begin{array}{rrr} -1&1&0&1&0&0 \\ 1&0&-1&0&1&0 \\ 0&-1&1&0&0&1 \end{array} \right] \;\;\;\;\;\; (3) \\ C &=& \left[ \begin{array}{rrr} 1&0&0&1&-1&0 \\ 0&1&0&-1&0&1 \\ 0&0&1&0&1&-1 \end{array} \right] \;\;\;\;\;\; (4) \end{eqnarray}
例えば, 接続行列 $A$ の第1列は上から順に $1, 0, 0, -1$ となっていますが, これは「枝1が節点④から出て, 節点①に向かうこと」を表しています.
キルヒホッフの電流則
上記の各行列を用いれば, 回路の特性をシンプルな形で表現することができます.
まず抑えておきたいことは, $A{\boldsymbol i}={\bf 0}$ は, どんな電流分布に対しても成り立つ, ということです（${\boldsymbol i}$ は電流分布ベクトル）.
これが成り立つのは $A{\boldsymbol i}={\bf 0}$ が正に「キルヒホッフの電流則」だからです. $A{\boldsymbol i}={\bf 0}$ の各行を取り出せば, 各節点におけるキルヒホッフの電流則になっていることが分かります.
同様に, $C{\boldsymbol i}={\bf 0}$ も常に成り立ちます. $A{\boldsymbol i}={\bf 0}$ が「各節点における」キルヒホッフの電流則であったのに対し, $C{\boldsymbol i}={\bf 0}$ は「各カットセットにおける拡張したキルヒホッフの電流則」を表します. これは前回記事で詳しく解説しました.
ちなみに, $B{\boldsymbol v}={\bf 0}$ が表すのは, キルヒホッフの電圧則です.
接続行列の rank
式2 と式4 を見比べると, 基本カットセット行列 $C$ は, 接続行列 $A$ の第4行を排除したものとなっています.
前回記事で示したように, 基本カットセット行列とは, 1次独立なすべてのカットセットの組を表したものです.
また, 接続行列が表しているものも一種のカットセットになっており, 式2 の第4行は他の行の線形結合（行基本変形）で表すことができます.
以上のことから節点が $n$個の連結グラフで表される回路において, 接続行列 $A$ の rank は 基本カットセット行列 $C$ の行数と等しく, $n-1$ です.
単位行列を含む特殊な構造
基本閉路行列 $B$ と, 基本カットセット行列 $C$ は共に特殊な構造を持っています. 基本閉路行列 $B$ は行列の右側部分が, 基本カットセット行列 $C$ は行列の左側部分がそれぞれ単位行列になっているのです.
そこで, それぞれの行列を以下のように表すことにします.
\begin{eqnarray} B= \left[ \begin{array}{c} B_m&I_l \end{array} \right] \;\;\;\;\;\; (5) \end{eqnarray}
\begin{eqnarray} C= \left[ \begin{array}{c} I_{n-1}&C_m \end{array} \right] \;\;\;\;\;\; (6) \end{eqnarray}
ここで, $I$ は単位行列, $B_m$ と $C_m$ はそれぞれ 基本閉路行列と基本カットセット行列から単位行列を除いた部分を表します.
$I$ の下付き文字が表すのは行列の行数（列数）です. $l$ は補木枝の数であり, 全枝数を $b$, 節点数を $n$ とすれば, $l=b-(n-1)$ となります. 枝や節点の数については前々回の記事で詳しく解説しました.
また, $B_m$ は $l \times (n-1)$, $C_m$ は $(n-1) \times l$ の行列です.
枝電流と閉路電流の関係
ここから本題である「閉路電流の根拠となる式」を示していきます.
具体的に示したいことは「キルヒホッフの電流則を満たすあらゆる電流分布は, 閉路電流によって表せる」ということです.
閉路電流の定義
まずは, 閉路電流を行列の形で表し, 閉路電流を定義しましょう.
図2 において, 閉路電流 ${\boldsymbol i}^1$ は,
\begin{eqnarray} {\boldsymbol i}^1 &=& [\begin{array}{r} -i^1&i^1&0&i^1&0&0 \end{array}]^T \\ &=& i^1[\begin{array}{r} -1&1&0&1&0&0 \end{array}]^T \;\;\;\;\;\; (7) \end{eqnarray}
のように表します. これは, 各枝電流を含む場合にはその方向に従って $\pm 1$ を, 含まれない場合には $0$ を, それぞれ対応する行に記したベクトルです. これが閉路電流の定義になります.
また, 式7 の係数ベクトルをよく見てみると, 基本閉路行列 $B$ の第1行を転置したものになっていることが分かります. 式7 を式3 と見比べてみてください.
このことから, 基本閉路行列 $B$ の第$k$行を ${\boldsymbol b}_k$ とおくと, 閉路電流 ${\boldsymbol i}^1$ は以下のように表すことができます（$T$ は行列の転置, 太字はベクトルを表すことに注意）.
\begin{eqnarray} {\boldsymbol i}^1 = {{\boldsymbol b}_1}^Ti_1 \;\;\;\;\;\; (8) \end{eqnarray}
その他の閉路電流についても同様です. 閉路電流 ${\boldsymbol i}^1$, ${\boldsymbol i}^2$, ${\boldsymbol i}^3$ と 基本閉路行列 $B$ の第1, 2, 3行は対応しています.
\begin{eqnarray} {\boldsymbol i}^k = {{\boldsymbol b}_k}^Ti_k \; (k = 1, 2, 3) \;\;\;\;\;\; (9) \end{eqnarray}
これはよく考えてみれば当たり前のことです.
閉路電流は閉路を元に定義されています. 閉路を定義した向きと同じ向きに電流を流したものが閉路電流であり, 閉路行列の行と同様の方法で定義されているのです.
つまり, 式9 は, 図2 で偶然このように表せたのではなく, 一般に成り立ちます. 閉路電流は, 閉路行列の行と対応しているのです.
閉路電流の満たす電流則
話は変わりますが, 図2 の閉路電流 ${\boldsymbol i}^1$ は,
\begin{eqnarray} A{\boldsymbol i}^1={\bf 0} \;\;\;\;\;\; (10) \end{eqnarray}
を満たします. 実際に計算してみましょう.
\begin{eqnarray} A{\boldsymbol i}^1 &=& \left[ \begin{array}{rrrr} 1&0&0&1&-1&0 \\ 0&1&0&-1&0&1 \\ 0&0&1&0&1&-1 \\ -1&-1&-1&0&0&0 \end{array} \right] \left[ \begin{array}{rrrrrr} -1\\1\\0\\1\\0\\0 \end{array} \right] \\ &=& \left[ \begin{array}{rrrr} -1+0+0+1+0+0 \\ 0+1+0-1+0+0 \\ 0+0+0+0+0+0 \\ 1-1+0+0+0+0 \end{array} \right] = \left[ \begin{array}{rrrr} 0\\0\\0\\0 \end{array} \right] = {\bf 0} \;\;\;\;\;\; (11) \end{eqnarray}
図2 の閉路電流 ${\boldsymbol i}^1$ については成り立つことが分かりましたが, 実は, 図2 の回路に限らず, 任意の閉路電流 ${\boldsymbol i}^x$ は $A{\boldsymbol i}^x={\bf 0}$ を満たします. これを示してみましょう.
まず, 閉路が節点$k$ を通らない場合, 閉路は節点$k$ につながる枝を含みません. このとき, $A{\boldsymbol i}^x$ の第$k$行の計算で, $A$ と ${\boldsymbol i}^x$ の要素の積はすべて零になります（式10 の第3行のような状況）.
続いて, 閉路が節点$k$ を含む場合を考えます. このとき, 閉路は節点$k$ に繋がる枝を 2つだけ含みます. これは, 閉路が「同じ節点を 2度通らない」という制約を持つためです.
この 2つの枝を, 枝$j$, $h$ とし, $A(k, j)$ と $A(k, h)$ が同符号の場合, すなわち, 枝$j$, $h$ が共に節点$k$ から流出する, もしくは, 共に流入するとき, 枝の向きに対する閉路の向きは一方の枝で一致し, 他方の枝で逆になります（※2）.
これは ${\boldsymbol i}$ の$j$要素と $h$要素が異符号であることを意味するため, $A(k, j)i_j+A(k, h)i_h=0$ となります. よって, このとき, $A{\boldsymbol i}$ の $k$要素は零です.
逆に, $A(k, j)$ と $A(k, h)$ が異符号の場合は, ${\boldsymbol i}$ の$j$要素と $h$要素が同符号となるため, こちらも $A(k, j)i_j+A(k, h)i_h=0$ となります. つまり, いかなる場合においても $A{\boldsymbol i}$ の $k$要素は零であり, 常に $A{\boldsymbol i}^x={\bf 0}$ が成り立ちます.
（※2） $A(k, j)$：行列$A$ の第$k$行$j$列の要素
電流則の一般解
上で, 任意の閉路電流 ${\boldsymbol i}^x$ について, $A{\boldsymbol i}^x={\bf 0}$ が成り立つことを示しました.
閉路電流は式9 のように閉路行列の行を転置したベクトルで表せるので, $A{\boldsymbol i}^1={\bf 0}$ は以下のように書き表すことができます.
\begin{eqnarray} A{{\boldsymbol b}_1}^Ti_1={\bf 0} \;\;\;\;\;\; (12) \end{eqnarray}
ここで基本閉路系に対応する $l$個の閉路電流を同時に環流させた場合, 回路全体での電流分布は,
\begin{eqnarray} {\boldsymbol i}={{\boldsymbol b}_1}^Ti_1+ \cdots +{{\boldsymbol b}_l}^Ti_l \;\;\;\;\;\; (13) \end{eqnarray}
となります. それぞれの閉路電流について, 式12 は成り立つので,
\begin{eqnarray} A({{\boldsymbol b}_1}^Ti_1+ \cdots +{{\boldsymbol b}_l}^Ti_l)={\bf 0} \;\;\;\;\;\; (14) \end{eqnarray}
も成り立ちます.
綺麗な形に整理しましょう. 新たに「閉路電流ベクトル」なるものを ${\boldsymbol i}_{loop}=[i^1 \cdots i^l]^T$ と定義すれば, 式14 は以下のように書き表されます.
\begin{eqnarray} AB^T{\boldsymbol i}_{loop}=0 \;\;\;\;\;\; (15) \end{eqnarray}
ここで登場した $B^T{\boldsymbol i}_{loop}$ とは何なのか, について考えてみます. 式15 の形を見れば, $B^T{\boldsymbol i}_{loop}$ が $A{\boldsymbol i}={\bf 0}$ の解であることは一目瞭然ですが, ただの解ではありません.
上述したように $A$ の rank は $n-1$ であるため, $A{\boldsymbol i}={\bf 0}$ は $b-(n-1)=l$個の一次独立な解を持ちます.
そして, ${\boldsymbol i}^k={{\boldsymbol b}_k}^T (k=1, \cdots , l)$ は, それぞれが $A{\boldsymbol i}={\bf 0}$ の一次独立な解の 1つであり, $B^T{\boldsymbol i}_{loop}={\boldsymbol i}^1+ \cdots +{\boldsymbol i}^l$ は, その一次独立な $l$個の解の線形結合となっています.
つまり, ${\boldsymbol i}=B^T{\boldsymbol i}_{loop}$ は $A{\boldsymbol i}={\bf 0}$ の一般解なのです.
よって, 電流則（$A{\boldsymbol i}={\bf 0}$）を満たすあらゆる電流は, 閉路を環流する複数の電流の線形結合として書き表せる, と言うことができます. これが閉路電流法の根拠です.
閉路電流と補木枝電流
上記の議論をすることで, 今後は気兼ねなく閉路電流法を使っていけるわけですが, 閉路電流という仮想的な電流については, 未だその正体が漠然として掴みどころがありません. 以下では, 閉路電流についてさらに深く掘り下げ, その正体に迫って参ります.
木枝電流と補木枝電流の定義
閉路電流と大変深い関係を持つのが, 補木枝電流です. 本サイトでは未出の用語ですので, ここで木枝電流と補木枝電流を定義します.
木枝電流 ${\boldsymbol i}_t$, 補木枝電流 ${\boldsymbol i}_c$ とは, その名の通り, 木枝を流れる電流と, 補木枝を流れる電流を指します. 木枝1 ~ 木枝n-1 を流れる電流を $i_1$ ~ $i_{n-1}$, 補木枝n ~ 補木枝b を流れる電流を $i_n$ ~ $i_b$ とすると, それぞれ以下のように表されます.
\begin{eqnarray} {\boldsymbol i}_t= \left[ \begin{array}{ccc} i_1 \\ \vdots \\ i_{n-1} \end{array} \right], {\boldsymbol i}_c= \left[ \begin{array}{ccc} i_n \\ \vdots \\ i_b \end{array} \right] \;\;\;\;\;\; (16) \end{eqnarray}
補木枝電流の性質
前回導出したキルヒホッフの電流式（$C{\boldsymbol i}={\bf 0}$）と式6, 式16 から, 木枝電流と補木枝電流について, 以下のような関係が導出されます.
\begin{eqnarray} \left[ \begin{array}{r} I_{n-1} & C_m \end{array} \right] \left[ \begin{array}{rr} {\boldsymbol i}_t \\ {\boldsymbol i}_c \end{array} \right] &=& 0 \\ I_{n-1}{\boldsymbol i}_t+C_m{\boldsymbol i}_c &=& 0 \\ {\boldsymbol i}_t &=& -C_m{\boldsymbol i}_c \;\;\;\;\;\; (17) \end{eqnarray}
式17 は, 「補木枝電流が与えられていれば, カットセット行列を用いて, 木枝電流が定まる」ということを意味します.
閉路電流の正体
話が各所に飛んで申し訳ありませんが, ここで閉路電流の話に戻ります.
式12 $A{{\boldsymbol b}_1}^Ti_1={\bf 0}$ より, $i_1$ はスカラーなので, $A{{\boldsymbol b}_1}^T={\bf 0}$ も成り立ち, これは一次独立な全ての閉路についても同様です. つまり,
\begin{eqnarray} A({{\boldsymbol b}_1}^T+ \cdots +{{\boldsymbol b}_l}^T)=AB^T={\bf 0} \;\;\;\;\;\; (18) \end{eqnarray}
が成り立ちます. これは, 電流則 $C{\boldsymbol i}={\bf 0}$ についても同じ結論になります. なぜならば, $C$ は $A$ の n-1行までを取り出した構造になっているためです.
\begin{eqnarray} CB^T={\bf 0} \;\;\;\;\;\; (19) \end{eqnarray}
式19 に式5 と 式6 を代入してまとめれば,
\begin{eqnarray} C_m+{B_m}^T={\bf 0} \;\;\;\;\;\; (20) \end{eqnarray}
という式を得ます. 行数や列数も上手く揃っています. ご確認ください.
ここで, 式20 と式17 より,
\begin{eqnarray} {\boldsymbol i}_t=-C_m{\boldsymbol i}_c={B_m}^T{\boldsymbol i}_c \;\;\;\;\;\; (21) \end{eqnarray}
また, ${\boldsymbol i}= \left[ \begin{array}{rr} {\boldsymbol i}_t \\ {\boldsymbol i}_c \end{array} \right]$ なので,
\begin{eqnarray} {\boldsymbol i}= B^T{\boldsymbol i}_c \;\;\;\;\;\; (22) \end{eqnarray}
が導かれます. よって, 「キルヒホッフの電流則を満たす電流の分布は, 補木枝電流と閉路行列で書き表せる」ということが分かりました.
この式22 を先に導出した ${\boldsymbol i}=B^T{\boldsymbol i}_{loop}$ と比較してみましょう.
どちらもキルヒホッフの電流則を満たす電流分布 ${\boldsymbol i}$ を表したものであり, $B^T$ の部分は共通になっています.
つまり, ${\boldsymbol i}_c={\boldsymbol i}_{loop}$ であり, 補木枝電流と閉路電流は全く同じものなのです.
別の言い方をしてみましょう. 補木枝電流 $i_n$, $\cdots$, $i_b$ が各補木枝に流れているときの回路全体の電流分布は, 各閉路に $i_n$, $\cdots$, $i_b$ という閉路電流を還流させたときの電流分布と全く同じになっています.
閉路電流は便宜上設定した仮想の電流に過ぎませんが, その実態は, 現実に補木枝を流れる電流と一致しているのです.
まとめ
以上, 閉路電流法についてでした. 結論をまとめます.
・${\boldsymbol i}=B^T{\boldsymbol i}_{loop}$ は, $A{\boldsymbol i}={\bf 0}$ の一般解であるため, あらゆる電流分布は, 閉路電流の線形結合で表すことができる. これが閉路電流法の根拠となっている.
・閉路電流と補木枝電流は同じものを表している.
高校でスルッと流した閉路電流ですが, ちゃんと考えると無視していた事実の多さに驚かされます. 今後も, 見えないものをスルーすることなく, 考え続けていきたい所存です. どうぞよろしく.
