正弦波交流が用いられる理由
一定周期で向きを変える電流を交流と呼び, 三角波, のこぎり波, 方形波など色々な種類があります.
しかしながら, 電線を流れる電流やコンセントから取り出される電流は世界中どこでも「正弦波」. 交流と言えばほとんどの場合に正弦波を指します.
ではなぜ正弦波なのでしょうか?
Table of Contents
発電
電気を作る方法は様々ですが, 太陽光発電を除いて, 多くの発電方式においては「発電機」が用いられます. 発電機による発電方法をざっくり説明すると以下の3ステップとなります.
- 燃料(石炭, ウラン, バイオエタノール etc…)を燃やしてタービンを回す
- 電磁誘導により起電力を得る
以下で詳しく説明します.

タービン
タービンの基本原理は風車を考えるとイメージしやすいでしょう.
タービンは流体の持つエネルギーを回転エネルギーに変換する装置です. 風車は風を吹き付けて回転エネルギーを作り出しますが, 火力発電や原子力発電では水を加熱し, 生じた高圧の水蒸気によってタービンを回します.
高圧の蒸気を吹き付けるのが通常のタービン(蒸気タービン)ですが, 燃料を爆発させたときのエネルギーを使う場合はガスタービンと呼ばれ, ガスタービンは飛行機の動力として使われます.
流体の種類により様々なタービンが存在し, 流体として水を使う場合は水力タービン, 風を使う場合は風力タービン, 平沢進の場合は世界タービンです.
電磁誘導
電磁誘導とは磁界の変化に伴って回路に起電力が生じる現象です. ここで生じる起電力は閉じた経路を通過する磁束の変化率に比例するという法則があり, これをファラデーの法則と呼びます.
磁束とは磁界によって生じる線の束のことです. 磁石のN極から出てS極に入り, 途中で消失することはありません. 磁束の密度は磁界の大きさに比例します. 磁束は仮想的な考え方で, 現実世界に「磁束」なるものがあるわけではありません.
この磁束が単位時間当たりにどれだけ変化するか, を表すのが「磁束の変化率」です.
ファラデーの法則を数式で表すと以下のようになります.
$$ V = \; – \frac{\Delta \Phi}{\Delta t} $$
ここで, \( V \) は生じる起電力, \( \Phi \) は磁束, \( t \) は時刻を表します. 閉ループ内の磁束を増やす向きを起電力の正の向きとしているため, 式中の「マイナス」は「磁束の変化を妨げる向きに起電力が生じること」を表しています.
なぜ正弦波なのか?
交流電流が一般に正弦波を指す理由の 1つは発電機によって生じる電流が「正弦波」であるためです.
では, 本当に正弦波になるのか, を以下で調べていきます.
電磁誘導による正弦波の発生
実際の発電は上で述べたタービンをくるくる回し, タービンにくっつけた強力な磁石によって磁界を変化させます. 則ち閉ループ回路は固定して, 磁界を変化させることで発電するわけですが, ここでは分かりやすさを優先して回すものを逆にします.
どういうことかと言うと, 磁界を固定して閉ループを回転させます(下図参照). すると閉ループを貫通する磁界が時刻と共に変化するというわけです. おそらく理系出身の方は高校で一度は見たことがある図でしょう.
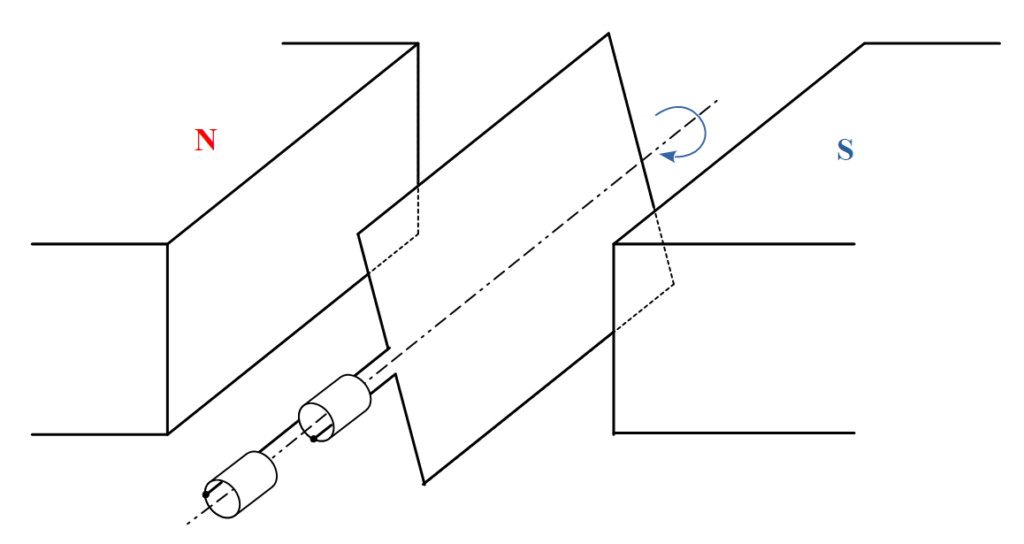
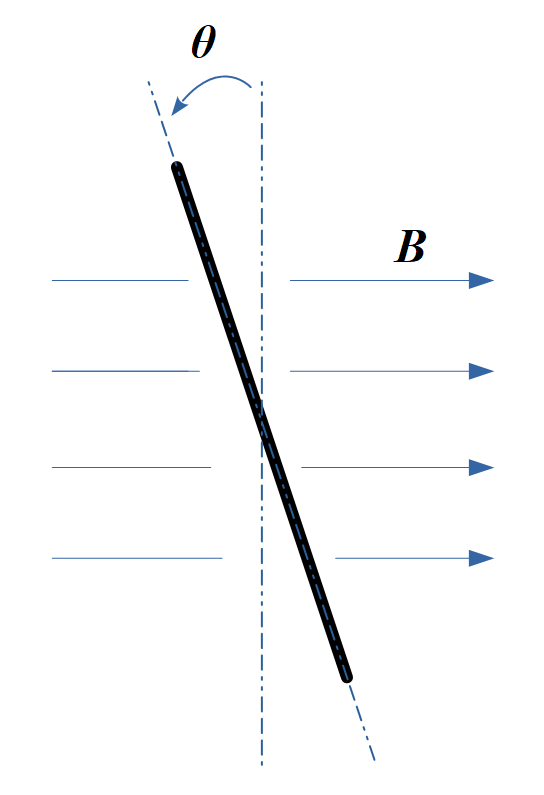
ここでは図中右向きに一定の磁界が存在します. 閉ループを通過する磁束 \( \Phi \) は磁束密度 \( B \) と閉ループの面積 \( S \) の積になります.
注意が必要なのは, 閉ループの回転によって通過する磁束が変化するということです. 閉ループ面と磁束の向きが直交している(閉ループを最も多くの磁束が通過する)状態を \( \theta = 0 \) とすると, \( \theta \) 傾いたときに閉ループ面を通過する磁束は以下のように表されます.
$$ \Phi = BS \cos{\theta} $$
微小な時間 \( \Delta t \) の間に閉ループ面が \( \Delta \theta \) だけ傾き, 磁束が \( \Delta \Phi \) だけ変化したとすると, ファラデーの法則から, 生じる起電力 \( V \) は以下のように計算できます.
\begin{eqnarray} V &=&\, – \frac{\Delta \Phi}{\Delta t} = \, – \frac{\Delta \Phi}{\Delta \theta} \cdot \frac{\Delta \theta}{\Delta t} \\ &\rm{ }& \\ &=& – \frac{BS \cos{(\theta + \Delta \theta)} – BS \cos{\theta} }{(\theta + \Delta \theta) – \theta } \cdot \frac{\Delta \theta}{\Delta t} \\ &\rm{ }& \\&=& BS \frac{2 \sin{ \frac{1}{2} (2 \theta + \Delta \theta ) } \sin{ \frac{1}{2} \Delta \theta } }{\Delta \theta} \cdot \frac{\Delta \theta}{\Delta t} \end{eqnarray}
\( \Delta \theta \) がゼロに近づくと,
$$ \sin{ \frac{1}{2} (2\theta + \Delta \theta) } \simeq \sin{\theta} \; , \; \sin{ \frac{1}{2} \Delta \theta \simeq \frac{1}{2} \Delta \theta } $$
なので,
\begin{eqnarray} V = BS \frac{2 \sin{\theta} \cdot \frac{1}{2} \Delta \theta }{\Delta \theta} \cdot \frac{\Delta \theta}{\Delta t} = BS \sin{\theta} \cdot \frac{\Delta \theta}{\Delta t} \end{eqnarray}
となります. ここで閉ループが一定の角速度 \( \omega \) で回転している場合には \( \Delta \Phi / \Delta t = \omega \) となり, コイルの初期角 \( \theta _0 \) を使って,
$$ \theta = \omega t + \theta _0 $$
と表されます. 上式を使うと, 起電力は以下のようになります.
\begin{eqnarray} V = \omega BS \sin{( \omega t + \theta _0 )} \end{eqnarray}
ご覧の通り, 発電機によって作られる起電力は正弦波の形になっていることが分かります. 本章冒頭にも述べた通り, 本来回転するのは磁石の方で, 実際の発電の様子とは幾分異なりますが, 原理はほぼ同じです. 実際の発電でも正弦波が作られます.
その他の理由
正弦波が用いられる理由は他にもあります.
その1つは「正弦波は線形回路によって形を変えない」というものです.
線形回路とは高校までで習ったような「抵抗」, 「キャパシタ」, 「コイル」などで構成される回路のことです(トランジスタやダイオードを含まない回路).
キャパシタに交流電圧を加えると出力される電流の波形は電圧を微分した形になります. 同様に, コイルに交流電圧を加えると電圧を積分した形の電流波形が得られるのですが, ご存じの通り, 正弦波(sin wave)は微分しても積分しても形が変わりません.
キャパシタやコイルを通過するときに波形の変化を一々考えなくてよい, ということが正弦波を使う利点の 1つです.
正弦波に関する用語
正弦波は
\begin{eqnarray} V = V_m \sin{( \omega t + \theta _0 )} \end{eqnarray}
という形で表されます.
ここで
・\( V_m \):振幅
・\( \omega t + \theta _0 \)(sin の中身):位相
・\( \omega \):角周波数
・\( \theta_0 \):初期位相
と呼びます.
$$ T= \frac{2 \pi}{\omega} $$
は波の一周に要する時間を表し「周期」と呼びます. 周期の逆数
$$ f= \frac{1}{T} = \frac{\omega}{2 \pi} $$
は「単位時間に繰り返される波の数」を表し, 「周波数」と呼びます. いずれも正弦波を扱う上で重要な用語です.
まとめ
「交流と言えば『正弦波』である」理由を簡単にまとめれば,
- 発電機で発電すると正弦波になるから
- 正弦波は線形回路で形を変えないから
ということになります. 特に2番が大きい.

