交流理論のための直流回路基礎

これから交流回路についてやっていくのですが, その前に直流回路の基本を押さえておこうと思います.

高校物理を修めた方向けにお話しするので, ミクロな話からスタートして, 回路の話に繋げます.

電流 / 電圧

電流

電流とは電子の流れのことであり, 以下の式で定義されます.

$$ I = \frac{dQ}{dt} \cdots (1)$$

ここで, \( I \) は電流, \( Q \) は電荷量, \( t \) は時刻です. 日本語にすると, 「単位時間当たりの電荷量の変化量」になります.

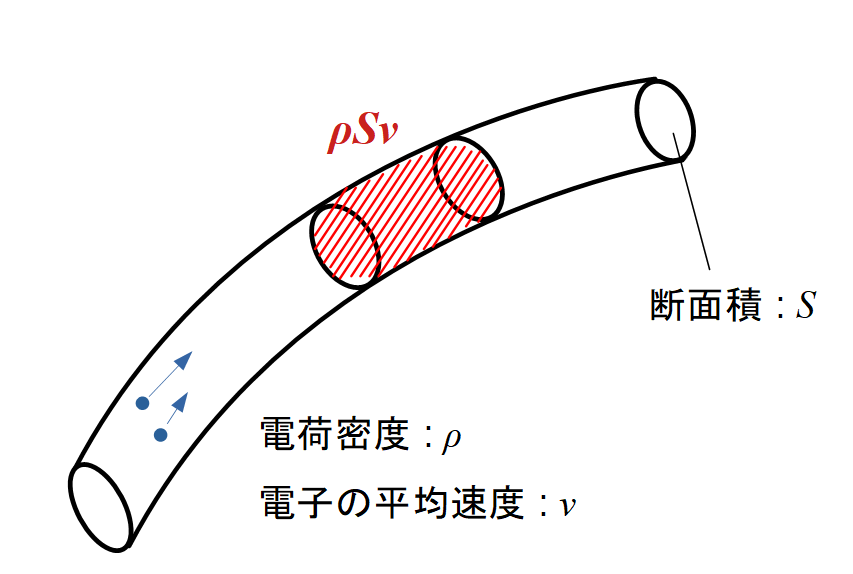
上の式は, 電荷密度 \( \rho \) , 導線の断面積 \( S \) , 電荷の平均速度 \( v \) を使って,

$$ I = \rho Sv \cdots (2)$$

と表すこともできます. 則ち, 電流とは, 「断面積 \( S \) の断面を単位時間あたりに通過する電荷の量」です.　

電位 / 電圧

電位とは, +1 クーロンの電荷が持つポテンシャルエネルギーです. 力学的位置エネルギーの「位置（高さ）」に対応するため, 中学校で初めて電圧と電流を学ぶときには, 電流を「水の流れ」, 電圧を「高さ」に例えて説明がなされます.

ポテンシャルエネルギーとは, 「潜在的に持っているエネルギー」のことです（日本語にしただけですが）. 電位 4 V のところにいる電荷が電位 0 V のところに落ちてくるまでにする仕事は, 電位 1 V のところにいる電荷が電位 0 V に落ちてくるまでにする仕事の 4倍になります.

高校で習った通り, 電位 \( V \) は「電場」によって作られます. 点電荷 \( Q \) から距離 \( r \) 離れた点での電位は, クーロン定数 \( k \) を使って,

$$ V= k \, \frac{Q}{r} \cdots (3) $$

と表されます. 電位は重ね合わせられるため, 周囲に複数電荷が存在すると, その分電位も増えます. 則ち, 「電位」とは「電荷密度」と関係しています.

電位の差を「電位差」と呼びます. この「電位差」のことを「電圧」と呼び, 電位差を作り出す装置が「電源」です. 上記の話をまとめると, 電源とは, 正極と負極の間に一定の「電荷密度の差」を作り出す装置であると言えます.

オームの法則 / 抵抗

電気回路の2点間の電位差と, その2点間を流れる電流の関係を表したものが「オームの法則」です.

$$ V= RI \cdots (4) $$

\( R \) は比例係数であり, 「抵抗」, もしくは「レジスタンス」と呼ばれます.

オームの法則は比例係数 \( G \)（ \( =R^{-1} \) ）を使って, 以下のように書くこともできます.

$$ I =GV \cdots (5) $$

この \( G \) を「電気伝導度」, もしくは「コンダクタンス」と呼びます.

開放 / 短絡

電気回路を断線することを「開放」, もしくは「オープン」と呼びます. 回路を開放することは, 「無限大の大きさの抵抗を挿入すること」と等価です. 抵抗が無限大ということはコンダクタンスは 0. よって, (5)式から, 流れる電流は 0 になります.

電源に抵抗を接続せず, 導線のみで回路を構成することを「短絡」, もしくは「ショート」と呼びます. 回路を短絡させることは, 「大きさ 0 の抵抗を挿入すること」と等価です. 抵抗が 0 ということはコンダクタンスは無限大であり, (5)式から, 電流も無限大になります.

電力 / エネルギー

起電力 \( E \) の電源を流れる電流が \( I \) のとき, \( E \) と \( I \) の積は単位時間当たりに外部にした仕事を表し, 「電力」と呼ばれます.

$$ P = EI $$

電力 \( P \) は単位時間当たりの仕事なので, 時間 \( t \) を掛ければその時間内に行った仕事を表します.

$$ (仕事) = Pt = EIt $$

キルヒホッフの法則

キルヒホッフの法則は「電流則」と「電圧則」の2つがあります.

キルヒホッフの電流則

キルヒホッフの電流則は, 「回路中の任意の節点に『流入する電流の総和』と『流出する電流の総和』が等しい」という法則です.

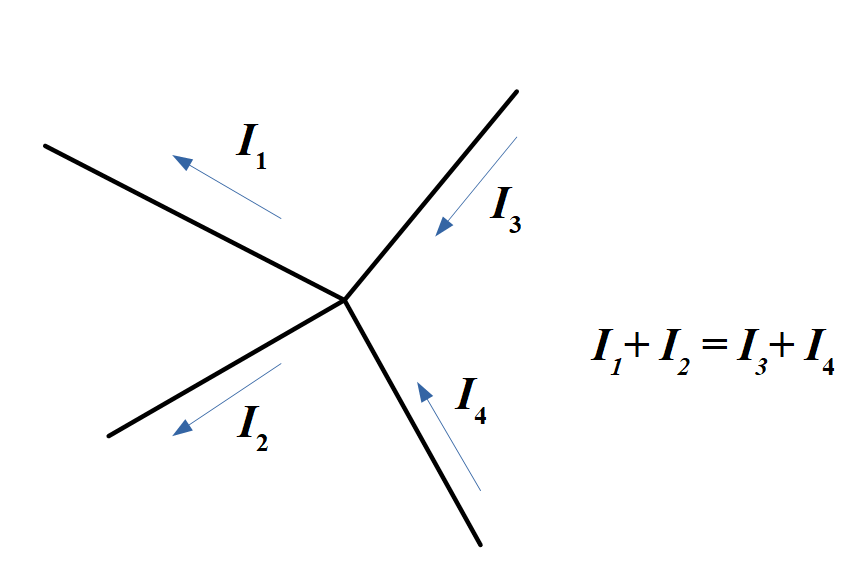
言われてみれば当たり前で, もし「節点に入る電流の方が出る電流より多い」場合, その節点には時間とともに電荷が蓄積されることになりますが, 回路中のただの節点にそのような能力はありません. 逆に, 「節点から出る電流の方が入る電流より多い」場合, どこかから電荷を作り出しているということになります. こちらも当然有り得ません.

キルヒホッフの電圧則

キルヒホッフの電圧則は「任意の閉回路おいて, 電位変化の総和がゼロ」という法則です.

雑な例を用いて説明します. 閉回路を環状線（railway でも road でも可）, 電位を標高とします. 環状線は多少の起伏がありまして, 登れば標高は高くなり, 下れば標高が低くなります. しかし, 環状線を一周して戻ってきたら, 元の高さに戻っているはずです. これがキルヒホッフの電圧則です. 電位も一周して戻ってくると元の電位になっています.

対称性

回路が対称な形をしているとき, 対称な部分には同じ現象が生じます.

回路が途中で2つの経路に枝分かれして, 2つの経路上の回路要素（抵抗など）が同じ場合, 2つの経路には同じ電流が流れる, ということです.

このような回路の性質を対称性と呼びます.

対称性を上手く使うことで, 回路の解析が容易になることがありまして, 以下でその例をご紹介します.

高校 or 大学入試で良く出題される回路の対称性を使った問題です.

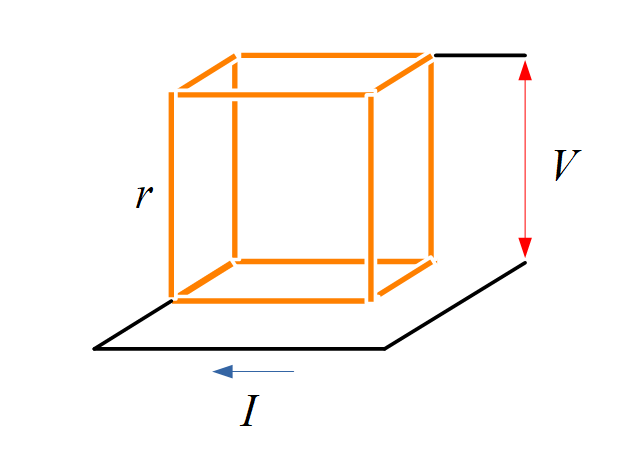
立方体の各辺が抵抗になっており, 各辺は \( r \) の抵抗値を持っています. ある頂点と, その頂点から最も離れた位置にある頂点との間に電圧 \( V \) を印加するとき, 電源を流れる電流はいくらでしょう, という問題です.

立方体を展開して平面の回路を考えても良いのですが, この問題には対称性を使った簡易な解法があります.

立方体の頂点に入る電流を \( I \) とすると, \( I \) は3つの辺に分かれるわけですが, この3つの辺は対称性を持っているので, 流れる電流はそれぞれ \( I/3 \) になります. 同様に次の辺に流れる電流は, 対称性より \( I/6 \) となり, その次の辺に流れる電流は \( I/6 + I/6 = I/3 \) です.

このようにすべての辺に流れる電流が分かります.

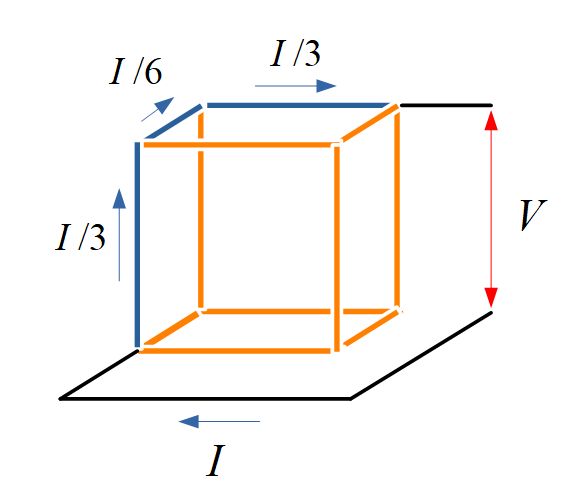
最後に, 図中青線の経路についてキルヒホッフの電圧則を適用すれば, (電源電圧) = (各辺での電圧降下の和) なので,

\begin{eqnarray} V &=& \frac{rI}{3} + \frac{rI}{6} + \frac{rI}{3} = \frac{5}{6} \, rI \\ I &=& \frac{6}{5r} \, V \end{eqnarray}

となります.

まとめ

電気回路のことを考えると混乱する人は多いと思うのですが, 電子, 密度, 時間と速さの関係などが分かっていれば, 意外と当たり前のことを言っていると気付きます.

中学や高校では, 電子や微分積分の知識が無かったために説明が難しかった電流や電圧も, 微積を学んだ後だとスムーズに導入可能です. 一度根本に立ち返って電流や電圧を見つめ直すことは電気回路についての理解を助けるものとなるでしょう.