実効値とは?交流の大きさに実効値を用いる理由
交流電圧, 交流電流は時刻とともに大きさと向きが変わるため, 直流電流と同じように大きさを決めることができません.
そこで登場するのが「実効値」です.

Table of Contents
実効値とは?
時間変化する値の大きさを規定するには「平均を取る」という方法があります. 「速さ」によく用いられる方法です.
しかし, 交流電流は時刻とともに「向き」も変化するため, 平均を取ると「大きさがゼロ」ということもあり得ます. 大きさを規定する方法として平均値は有効とは言えません.
そこで用いられるのが, 実効値です. 実効値は「各瞬時値の2乗の平均の平方根」を指します. 英語では Root Mean Square (RMS) と呼びます.
実効値の計算のためには, まず, 交流電流(もしくは電圧)を2乗します. 瞬時値が負の値を取ろうとも, 2乗すればすべて正の値となります. その後平均を取って, 最後に2乗した分を打ち消すため, 平方根(ルート)を取ります.
交流電流の実効値 \( I_R \) を数式で表すと以下のようになります. 比較のために, 平均値 \( I_A \) を併記します.
\begin{eqnarray} 平均値: I_A &=& \frac{1}{T} \int_{0}^{T} i dt \\ \\ 実効値: I_R &=& \sqrt{ \frac{1}{T} \int_{0}^{T} i^2 dt } \end{eqnarray}
ここで \( i \) は交流電流, \( t \) は時刻, \( T \) は周期を表します.
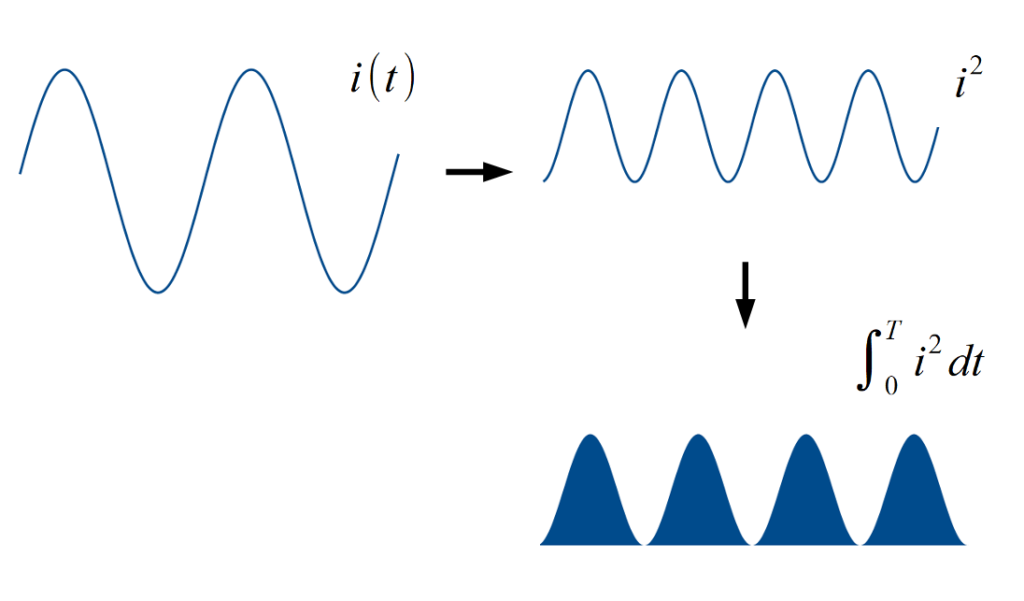
電力と実効値
電流, 電圧の実効値をこのように定義するには理由があり, それは電力と関係しています.
ある抵抗 \( R \) に直流電流 \( I \) を流したときの消費される電力 \( P \) は以下のように表されます.
$$ P= RI^2 $$
同様にして, 抵抗 \( R \) に交流電流 \( i \) を流したとき, 消費される平均電力 \( P_e \) は
$$ P_e = \frac{1}{T} \int_{0}^{T} R i^2 dt $$
上で述べた実効値を使って交流電流の平均電力を表記すると
$$ P_e = R {I_{R}}^{2} $$
となり, 直流電流を流した場合とほぼ同じ形に表せます. 上式から「交流電流の実効値」と「直流電流の大きさ」が同じであれば, 同じ電熱効果を生むことが分かります.
つまり, 電流の実効値とは 「交流電流を流したときと同じ電力が消費される直流電流の大きさ」を表しているのです.
様々な波形の実効値
交流には様々な形が存在します. 最もよく使われるのは正弦波ですが, デジタル回路を扱う際には方形波を用いますし, 交流を直流に変換する際には回路中に半波整流波が生じます.
一般家庭で使われる交流電流が正弦波交流である理由については, 以下記事もご参照ください.
交流の実効値は毎回定義から計算しても良いのですが, 波の形(正弦波, 三角波, 方形波 など)が分かっていれば, 振幅によって実効値が決まります.
実際に, 色々な波形の実効値を計算していきたいと思います. 計算を簡単にするため, 波の振幅はすべて \( I_m \) , 周期はすべて \( T \) とします. 振幅については実は色々と定義があるのですが, 今回は波の最大値と波の中心(平均値)の差を振幅とします.
正弦波
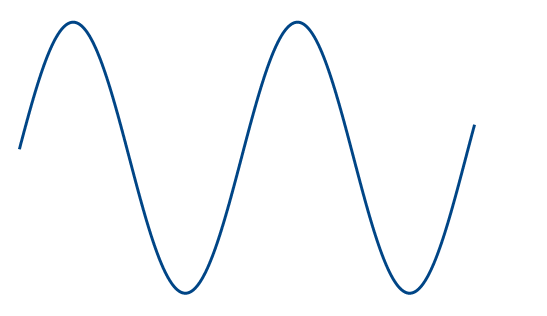
正弦波とは sin関数の形の波です. 式で書くと以下のようになります.
$$ i(t) = I_m \sin \, \omega t $$
\( \omega t \rightarrow \theta \) と変数変換して実効値を計算します.
\begin{eqnarray} I_R &=& \sqrt{ \frac{1}{T} \int_{0}^{T} i^2 dt } \; = \; \sqrt{ \frac{1}{2 \pi} \int_{0}^{2 \pi} i^2 d\theta } \\ &\rm{ }& \\ &=& \sqrt{\frac{1}{2 \pi} \int_{0}^{2 \pi} {I_m}^{2} \sin^2 \theta d \theta } \\ &\rm{ }& \\ &=& I_m \sqrt{\frac{1}{2 \pi} \int_{0}^{2 \pi} \frac{1}{2} (1- \cos \, 2 \theta) d \theta } \\ &\rm{ }& \\ &=& I_m \sqrt{ \frac{1}{2} – \frac{1}{4 \pi} \int_{0}^{2 \pi} \cos \, 2 \theta d \theta } \\ &\rm{ }& \\ &=& I_m / \sqrt{2} \end{eqnarray}
三角波
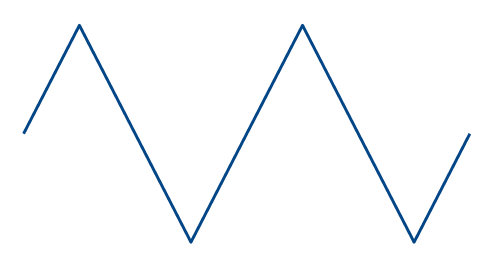
三角波の形はパッと見正弦波に似ていますが, 直線のみからなり, 所々滑らかではありません. 式で書くと以下のようになります.
\begin{eqnarray} i(t) = \left\{ \begin{array} \, \frac{T}{4} I_m \cdot t &\rm{ }& \;\; ( 0 \leq t < \frac{T}{4} ) \\ – \frac{T}{4} I_m \cdot t + 2 I_m &\rm{ }& \;\; ( \frac{T}{4} \leq t < \frac{3T}{4} ) \\ \frac{T}{4} I_m \cdot t -4Im &\rm{ }& \;\; ( \frac{3T}{4} \leq t < T ) \end{array} \right. \end{eqnarray}
実効値は以下のように計算できます.
\begin{eqnarray} I_R &=& \sqrt{ \frac{1}{T} \int_{0}^{T} i^2 dt } \\ \\ &=& \sqrt{ \frac{4}{T} \int_{0}^{T/4} \left( \frac{4}{T} \right)^2 {I_m} ^2 \, t^2 dt } \\ \\ &=& I_m \sqrt{ \left( \frac{4}{T} \right)^3 \frac{1}{3} \, \left[ t^3 \right]_{ \, 0} ^{ \, T/4 } } \\ \\ &=& I_m \sqrt{ \left( \frac{4}{T} \right)^3 \frac{1}{3} \left( \frac{T}{4} \right)^3 } \\ \\ &=& I_m / \sqrt{3} \end{eqnarray}
方形波
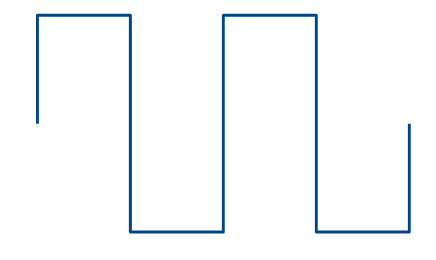
方形波(矩形波)はデジタル回路でよく用いられ, 2進法の 0 と 1 を電流の高低で表現します. 式で書くと下のようになります.
\begin{eqnarray} i(t) = \left\{ \begin{array} \, I_m \; ( 0 \leq t < T/2 ) \\ -I_m \; ( T/2 \leq t < T ) \end{array} \right. \end{eqnarray}
実効値の計算は非常に簡単です. というより計算しなくても分かりますよね.
\begin{eqnarray} I_R &=& \sqrt{ \frac{1}{T} \int_{0}^{T} i^2 dt } \\ \\ &=& \sqrt{ \frac{2}{T} \int_{0}^{T/2} {I_m} ^2 dt } \\ \\ &=& I_m \sqrt{ \frac{2}{T} \cdot \frac{T}{2} } \\ \\ &=& I_m \end{eqnarray}
方形波というと, off のときの値が 0 の波を指す場合もあります. その場合には on時間 と off時間 の比率によって実効値が変わってきます.
半波整流波
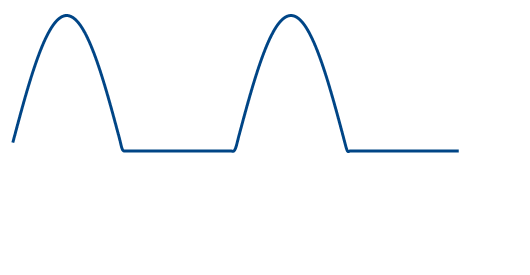
整流とは交流を直流にすることです. ダイオードに交流電流を流すと順方向の電流のみが取り出され, 半端整流波ができます. 半端整流は以下のように表せます.
\begin{eqnarray} i(t) = \left\{ \begin{array} \, I_m \sin{\omega t} \;\; ( 0 \leq t < T/4, T/2 \leq t < 3T/4 ) \\ 0 \;\; ( T/4 \leq t < T/2, 3T/4 \leq t < T ) \end{array} \right. \end{eqnarray}
実効値は (正弦波の実効値) \( / \sqrt{2} \) になります.
\begin{eqnarray} I_R = I_m /2 \end{eqnarray}
まとめ
今回の内容です.
- 実効値の定義と計算方法
- 実効値の意味
- 様々な波形の実効値計算

