フェーザ表示の活用:複素インピーダンス
コイルやキャパシタに交流電圧を印加すると, 電流の位相が電圧に対して遅れたり, 進んだりするため, 直流回路で学んだことだけでは解析が困難.
こうした解析に便利なのが「フェーザ表示」と「複素インピーダンス」です.
本稿では, 複素インピーダンスを導出することを目指します.

Table of Contents
線形素子の電流 – 電圧特性
複素インピーダンス導出の準備として, 各線形素子(抵抗, コイル, キャパシタ)の電流 – 電圧特性について考えます.
抵抗
オームの法則は定常状態(直流印加時)における電流 – 電圧特性のみならず, 交流動作下の各瞬時においても成立します.
また, 抵抗に印加された交流電圧に対し, 交流電流の位相は変化しません.
よって, 抵抗 \( R \), 交流電圧 \( v \), 交流電流 \( i \) の関係は直流印加時と同じです.
$$ v (t)= \, R \, i (t) \; \cdots \; (1) $$
コイル(インダクタ)
抵抗と同じように, コイルでも交流電圧印加時の電流 – 電圧特性をみていきましょう. コイルとは導線を円筒形に巻いた素子です.
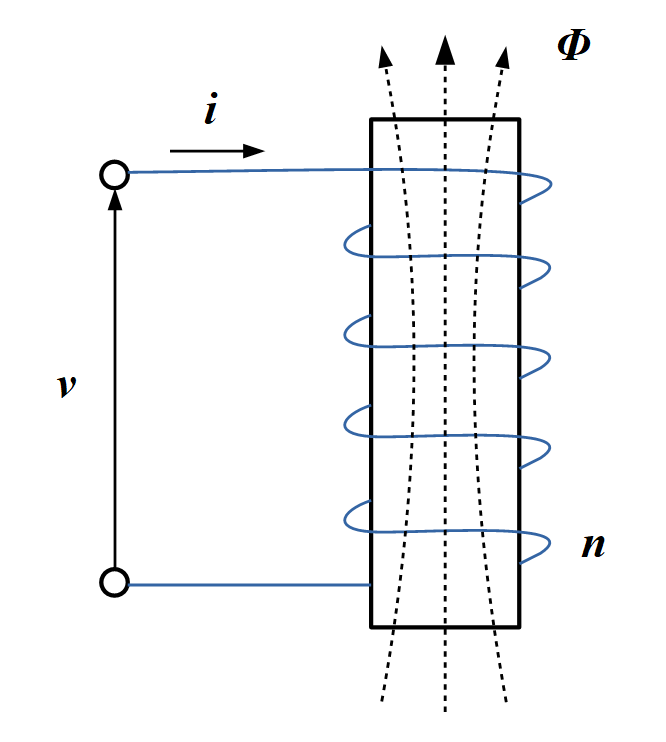
上図のように, \( n \) 回巻のコイルに電流 \( i \) を流すと電流の大きさに比例して, コイルを通る磁束 \( \Phi \) が生じます.
$$ \Phi \, (t) = A \; i (t) \; \cdots \; (2) $$
\( A \) は 比例定数です.
コイルから磁束の漏れが無いと仮定して, 電流が変化するとき, (2)式より磁束が変化します. ファラデーの電磁誘導の法則より, コイルを貫く磁束が時間で変化するとき, 起電力 \( v \) が生じます.
$$ v = \, n \, \frac{d \Phi}{dt} \; \cdots \; (3) $$
\( v \) はコイルの磁束変化を妨げる向きなので, 上図の \( v \) の矢印の向きです.
(2), (3)式より, コイルを流れる電流とコイル両端にかかる電圧の関係式が導かれます.
$$ v = \, nA \frac{di}{dt} \; \cdots \; (4) $$
\( nA=L \)(インダクタンス)と置くと,
$$ v= \, L \frac{di}{dt} \; \cdots \; (5) $$
です. コイル自身の電流の変化により, 電圧が誘導されるため, この現象を自己誘導と呼びます.
キャパシタ
キャパシタとは 2枚の平面電極を平行に配置した素子です.
キャパシタの両端に電圧を印加すると, 印加する電圧 \( v \) の大きさに比例して電荷 \( q \) が誘起されます.
$$ q(t) = \, C \, v (t) \; \cdots \; (6) $$
\( C \)(キャパシタンス)は平行平板の構造と平板間の物質に依存する定数です.
印加電圧が変化すると, 平行平板に蓄積された電荷量の変化に伴って, 電極間には変位電流 \( i \) が流れます.
$$ i(t) = \, \frac{dq}{dt} \; \cdots \; (7) $$
(6), (7)式より, キャパシタを流れる電流と両端にかかる電圧の関係式が導出可能です.
$$ i = \, C \frac{dv}{dt} \; \cdots \; (8) $$
以上, 抵抗, コイル, キャパシタそれぞれについて電流 – 電圧特性を導出することができました.

複素インピーダンスの導出
導出した電流 – 電圧の関係式から各素子の複素インピーダンスを導出していきます.
複素インピーダンスとは
複素インピーダンスを導出する前に, 複素インピーダンスとは何かという話をします.
直流回路において, 抵抗を流れる電流 \( I \) と抵抗の両端にかかる電圧 \( V \) は抵抗の大きさ \( R \) を比例定数として以下のように結ばれます.
$$ V= RI \; \cdots \; (9) $$
交流回路において, (9)式の \( R \) に相当する比例定数が「インピーダンス」です. 則ち, 交流電流 \( i \), 交流電圧 \( v \) とインピーダンス \( Z \) の関係は以下のように表されます.
$$ v = Z i \; \cdots \; (10) $$
しかしながら, 実数(つまり三角関数)で書かれた正弦波交流では, コイルやキャパシタのインピーダンスを綺麗に表記できません. 高校で実数のインピーダンスについては学んだかもしれませんが, 高校で学ぶ実数のインピーダンスで計算できるのは「交流の大きさ」だけであり, 「位相の変化」を表現できませんでした.
対して, 交流電圧, 交流電流を複素数で表記(フェーザ表示)すると, 位相の変化も綺麗に表現でき, インピーダンスをシンプルに書き表すことが可能です.
フェーザ表示した複素電流, 複素電圧を関係付けるインピーダンスもまた複素数となり, これを「複素インピーダンス」と呼びます.
(10)式より, 複素インピーダンスは複素電圧を複素電流で割れば導出できることが分かります. 以下では, 抵抗, コイル, キャパシタの各複素インピーダンスを導出していきましょう.
抵抗
抵抗の複素インピーダンス \( Z_R \) は直流回路と同じです.
$$ \dot{Z_R} = R \; \cdots \; (11) $$
コイル
虚数単位を \( j \), 交流電流の振幅を \( I_m \), 位相を \( \theta = \omega t + \varphi \) として, 電流をフェーザ表示します.
$$ \dot{I} = \, I_m \, exp (j \theta) \; \cdots \; (12) $$
(12)式を (5)式に代入すると,
$$ \dot{V} = \, L I_m \frac{d \, exp (j \theta)}{dt} = \, jL \, I_m \, exp (j \theta) \, \frac{d \theta}{dt} $$
\( d \theta / dt = \omega \)(角周波数)であり, \( \dot{I} = \, I_m \, exp (j \theta) \) なので,
$$ \dot{V} = j \omega L \, \dot{I} \; \cdots \; (13) $$
となり, インダクタンス \( L \) のコイルの複素インピーダンス \( Z_L \) は
$$ \dot{Z_L} = \dot{V} / \dot{I} = j \omega L \; \cdots \; (14) $$
であることが分かりました.
キャパシタ
交流電圧の振幅を \( V_m \), 位相を \( \theta = \omega t + \varphi \) とすると, 電圧のフェーザ表示は以下の形になります.
$$ \dot{V} = \, V_m \, exp (j \theta ) \; \cdots \; (15) $$
(15)式を (8)式に代入すると,
$$ \dot{I} = \, C V_m \frac{d \, exp (j \theta ) }{dt} = \, jC \, V_m \, exp (j \theta) \, \frac{d \theta}{dt} $$
\( d \theta / dt = \omega \)(角周波数)であり, \( \dot{V} = \, V_m \, exp (j \theta ) \) なので,
$$ \dot{I} = j \omega C \, \dot{V} \; \cdots \; (16) $$
よって, キャパシタンス \( C \) のキャパシタの複素インピーダンス \( \dot{Z_C} \) は以下のように求められます.
$$ \dot{Z_C} = \dot{V} / \dot{I} = \left( j \omega C \right)^{-1} \; \cdots \; (17) $$
複素インピーダンスの性質
複素インピーダンスは直流回路の「抵抗」に相当する概念ですので, 抵抗と似ているところもあれば, 複素数であるためにただの抵抗と異なるところも多々あります.
複素インピーダンスの持つ諸性質について解説していきます.
インピーダンスの合成
直流回路では「複数の抵抗をまとめて1つの抵抗と考える」=「合成抵抗」という考え方がありました.
そのとき注意すべきは直列回路と並列回路で合成抵抗の計算方法が異なることです.
直列に接続された複数の抵抗はそのまま足せばよかったのですが, 並列に接続された抵抗は「逆比の和」で計算します.
複素インピーダンスの合成も直流回路の抵抗の場合と全く同じです. 直列回路は通常の和, 並列回路は逆比の和です.
複素インピーダンスの大きさと位相
複素インピーダンス自体は複素数なので「大きさ」はありません.
「複素インピーダンスの大きさ」と言う場合には「複素インピーダンスの絶対値」を意味します.
複素インピーダンス \( \dot{Z} \) を極座標で表すと,
$$ \dot{Z} = | \dot{Z} | \, exp (- j \theta) $$
と書けます. ここで \( | \dot{Z} | \) は複素インピーダンスの大きさ, \( \theta \) は複素インピーダンスの位相を表します.
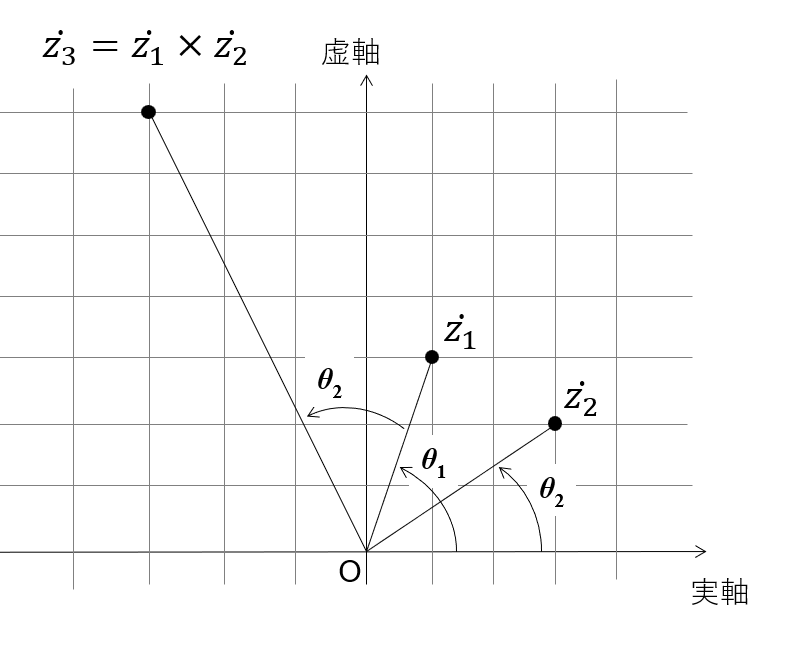
複素平面上で眺めると, 極座標表示した複素数の掛け算は「複素平面上の座標の回転と拡大」を表していることが分かります.
参考:複素数の極形式と回転
複素インピーダンスの大きさは, 交流電圧と交流電流の大きさ(実効値や振幅)の関係を表します.
$$ | \, \dot{V} \, | = \, | \, \dot{Z} \, | \, \cdot \, | \, \dot{I} \, | $$
対して, 複素インピーダンスの位相は「電圧の位相に対し, 電流の位相をどれだけシフトさせるか」を表しています.
コイルならば \( \theta = \, \pi / 2 \), キャパシタならば \( \theta = \, – \pi /2 \) となります.
インピーダンスの周波数依存性
コイルやキャパシタの複素インピーダンスを見ると分かる通り, \( \omega \)(角周波数)が入っています. これは交流電圧の角周波数です.
つまり, 入力交流電圧の角周波数が変化すると, 複素インピーダンスの大きさが変化します.
コイルの複素インピーダンスの大きさは角周波数に比例するため, 電源電圧の周波数が大きくなると, 複素インピーダンスは大きくなっていきます. つまり電流は流れにくくなります.
一方, キャパシタの複素インピーダンスの大きさは角周波数に反比例します. つまり, 電源電圧の周波数が大きくなると複素インピーダンスは小さくなっていき, 電流が流れやすくなります.
まとめ
以上, 複素インピーダンスの導出とその性質についてでした.
次回は, 「複素インピーダンスの図示」について考えつつ, 複素インピーダンスのイメージを確立していきたいと考えております.

