オイラーの公式の利用
オイラーの公式がファイマンをして「我々の至宝だ」と評されるのは, 形の「美しさ」や「数学上の発展」に寄与したためだけではありません.
オイラーの公式の優れた点は, 数学上の応用に留まらず, 電磁気, 量子力学, 結晶構造解析など, 物理学の様々な分野へ応用されているためです. 最近ではディープラーニングにも複素数を応用して, 「複素ニューラルネットワーク」なるものも研究されているとか.
これらすべての応用はオイラーの公式無しにはあり得なかった話です.
今回はオイラーの公式が寄与した物理分野と, どのように寄与したのかをざっくりと紹介していきます.
Table of Contents
オイラーの公式とは
オイラーの公式は複素指数関数と三角関数を結びつける以下の等式を示します.
$$ e^{ix} = \cos{x} +i \sin{x} $$
18世紀, レオンハルト・オイラーによって導出されました.
その歴史と証明方法については以下の記事にて解説しました.
以下では, オイラーの公式の応用, 利用について述べます.
波の記述
波を書き表すためには三角関数が使われますが, オイラーの公式によって三角関数と指数関数の相互変換が可能となり, 指数関数を用いて波を書き表すことができるようになりました.
波の記述に指数関数を用いると,
- 微分, 積分しても形が変わらず, 計算が楽
- 位相を振幅で表現できる
という利点があります.
オイラーの公式は上記利点により, 「波」を扱う様々な分野の発展に寄与しました.
量子力学
量子力学の始まりは「物質は粒子であり, 波でもある. 量子なのだ.」という発見でした.
20世紀初頭には, プランクによる黒体放射の研究やアインシュタインによる光電効果の発見がなされ, ミクロな世界ではマクロな世界で決して想像し得ない物理現象が起きていることが既知となりました.
ミクロな世界においてはあらゆるものが粒子としての性質と波動としての性質を併せ持ちます.
故に, マクロな世界で粒子の運動を完全に表現することができた「ニュートンの運動方程式」はミクロな世界の力学においては役に立ちません. 代わりに量子の運動を記述するのが「波動方程式」です.
波動方程式は波について記述する微分方程式なのですが, 微分や積分によって形を変えないという指数関数の性質は, 波動方程式を解く上で非常に役に立ちます.
電磁気, 電気回路
無線通信に用いる電波や光, 家庭用コンセントから流れる交流電流などはすべて波です. 波があるところにオイラーの公式あり.
アンテナの設計や電気回路設計に応用されており, 複素数が日常生活に最も役立っている分野ではないかと思います.
結晶構造解析
結晶とは, 原子 (または分子)が規則正しく並んだ固体のことです. 結晶にX線という透過性の高い光を当てると, 反射したX線の強度と位相から結晶の構造を決定することができます.
光 (つまり波)を使っているので, ここにも複素数が現れ, オイラーの公式が活躍します.
結晶構造解析にはもう1つ波が登場します. ありのまま, やっていることを話すと, 結晶構造解析の分野では, 周期的に並んだ原子 (または分子)の列を「波」と見なします.
ディープラーニング：複素ニューラルネットワーク
最近では, 複素ニューラルネットワークというものが現れたと聞き及んでいます. ニューラルネットワークとは動物の脳細胞 (ニューロン)とそれを繋ぐ筋線維 (シナプス)をモデルとした機械学習モデルです.
人間の脳細胞を通過する信号は電気信号で, 通常のニューラルネットワークプログラム中を伝わる信号は実数なのですが, 複素ニューラルネットワーク中を流れるのは複素数です. 入力データが複素数で表せるものへと適用すると効率的に機械学習を行えます.
2次元の画像をフーリエ変換すれば複素数が現れ, 複素数は座標の回転, 拡大や縮小を自然に扱うことができるため, 複素ニューラルネットワークの活用により, ディープラーニングが得意とする画像解析がさらに進展する可能性にも期待されます.
フーリエ変換
フーリエ変換を一言で説明するのは大変なので, ここでは説明は避け, 「何ができるのか」という点に焦点を絞りますれば, 以下のようなことができる操作と言えるかと.
- 微分方程式を解くのが簡単になる
- 「時間で表された波」を「周波数で表された波」に変換することができる
1つ目の特徴は先ほども述べた波動方程式や, 熱伝導方程式など, 様々な微分方程式を解くことを容易にしてくれます.
2つ目は, 下の図を見てもらうのが一番分かりやすいかと.
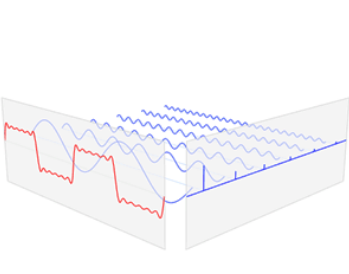
フーリエ変換についての Wikipedia の記事から引用しました (パブリックドメインです). Wikipedia は一般的に正しいことを書いているので, お世辞にも初心者にとって分かりやすいとは言えませんが, このアニメーションは素晴らしいですね. 大学の授業の100倍分かりやすいです. 多くの方の理解の助けになるかと.
人間の肉声や, ギターの音, その他自然界にある音のほとんどは, 様々な周波数の音の足し合わせでできています (上図左側赤線). それらの音を周波数ごとに分解し (上図右側青線), 各周波数の音がどれだけ含まれているかを調べることができるのが, フーリエ変換という数学的操作です.
電子機器から出力された電気信号をフーリエ変換して, 周波数ごとに分解すれば, 電子機器の中身の回路を予測し, 不具合が無いか調べることができますし, 橋の支柱をハンマーで叩いて返ってきた音をフーリエ変換すれば, 橋の支柱を壊すことなく (非破壊に), 異常を検知することができます.
回転
複素数は, 平面上の点の座標の回転を表すことが得意で, オイラーの公式を使えば, 座標の回転を簡単に表すことができます.
複素数を使ったときには平面上の点の回転を表すことができるのですが, 複素数を拡張した四元数を使えば, 3次元空間において, とある軸周りの回転を表すことができます.
回転を上手に表すことができる性質は結晶学, 群論の表現に寄与し, 3DCGなどにも応用されています.
まとめ
オイラーの公式とは複素解析の基礎を形作ったものであり, 複素数で扱われる, あらゆるモノに寄与しました. そして複素数の応用として代表的なものが, 「波の扱い」, 「フーリエ変換」, 「回転」です.
オイラーの公式が活躍する分野は, ここで書かれていない応用も多々あると思います.
それらを見つけて, 上手く説明できるようになったら, 追記しようと思います.
