フーリエ級数展開とは何か？ (マクローリン展開とのアナロジーでざっくり解説)

フーリエ級数展開は, 熱伝導方程式や波動方程式で現れる「偏微分方程式」の解を求めること, また, フーリエ変換に応用されます.

そんなフーリエ級数展開ですが, フーリエ級数展開した関数と展開する前の関数が一致することの証明は兎角面倒で, フーリエ級数展開の理解を妨げる原因となっております.

思うに, 「フーリエ級数展開とは何か？」を理解するにあたって, フーリエ級数展開の細かな証明など, 必要ないのではないでしょうか？まずはフーリエ級数展開の何たるか, をざっくり理解した後に証明をやった方が効率的です.

ということで, この記事ではフーリエ級数展開の証明はやらず, マクローリン展開と比較しつつ, 「フーリエ級数展開とは何か？」という点のみを解説していきます.

マクローリン展開とは何か？

マクローリン展開とは \( x^n \) の無限線形和によって関数を表すことを指します.

よく用いられる例を挙げましょう.

三角関数

$$ \sin{x} = \sum_{n=0}^{\infty} \frac{ (-1)^n }{ (2n+1) ! } x^{2n+1} $$

$$ \cos{x} = \sum_{n=0}^{\infty} \frac{ (-1)^n }{ (2n) ! } x^{2n} $$

指数関数

$$ e^x = \sum_{n=0}^{\infty} \frac{x^n }{n!} $$

それぞれ右辺がマクローリン展開された式です. 一般に関数 \( f(x) \) に対するマクローリン展開は以下のように表されます.

$$ f(x) = \sum_{n=0}^{\infty} \frac{ f^{(n)} (0) }{n!} x^n $$

マクローリン展開はオイラーの公式を始めとして, 数学上重要な様々な証明に用いられます. マクローリン展開は原点を中心に展開を行いますが, 一般形であるテイラー展開は点a の周りで関数を展開する操作です.

非線形な関数を \( x^n \) の多項式に変換できるため, 関数を近似したり, 計算機を用いた計算を容易にしたりと, 広く応用されます.

マクローリン展開, テイラー展開についての詳細はこちらをご覧ください.

テイラー展開, マクローリン展開とは何か？

フーリエ級数展開とは何か？

マクローリン展開では \( x^n \) によって関数を展開しましたが, 関数の無限和による表現方法は他にもあります.

その1つが, 三角関数 \( \sin{(nx)} \), \( \cos{(nx)} \) を用いた展開方法で, この三角関数を用いた展開が「フーリエ級数展開」です.

つまり, フーリエ級数展開とは, 元の関数 \( f(x) \) を次のように変形することを指します.

$$ f(x) = \frac{a_0}{2} + \sum_{n=1}^{\infty} ( a_n \cos{nx} + b_n \sin{nx} ) $$

\( a_n \), \( b_n \) は各項の係数であり, それぞれ cos関数と sin関数にくっついているので, \( a_n \) をフーリエ余弦係数, \( b_n \) をフーリエ正弦係数と呼びます.

注意点として, 三角関数を用いて展開するには制約があります. 三角関数は周期性を持っているので, 通常, 周期関数の展開に用いられます.

任意関数をフーリエ級数展開する方法

では, 実際に任意の周期関数をフーリエ級数展開するにはどうすれば良いでしょう. 周期 \( 2 \pi \) の実数関数 \( f(x) \) について考えます.

結論から言えば, 各項の係数は以下になります.

$$ a_n = \frac{1}{ \pi } \int_{-\pi}^{\pi} f(t) \cos{nt} dt, $$

$$ (n=0, 1, 2, 3, \cdots) $$

$$ b_n = \frac{1}{ \pi } \int_{-\pi}^{\pi} f(t) \sin{nt} dt, $$

$$ (n=1, 2, 3, \cdots) $$

このようにすると, フーリエ級数展開の係数を決定することができますが, なぜこうなるのか？というのが, フーリエ級数展開の難しいところです. これは別記事で解説します.

フーリエ級数展開の例

簡単な例で, 実際にフーリエ級数展開をやってみたいと思います.

対象とするのは周期 \( 2 \pi \) の「方形波」です.

\begin{eqnarray} f(x) = \left\{ \begin{array}{l} – 1 \;\; ( – \pi \leq x < 0) & \\ 1 \;\; (0 \leq x < \pi ) & \end{array} \right. \end{eqnarray}

フーリエ余弦係数, 正弦係数をそれぞれ求めていきます.

\begin{eqnarray} a_n &=& \frac{1}{ \pi } \left\{ – \int_{-\pi}^{0} \cos{nt} dt + \int_{0}^{\pi} \cos{nt} dt \right\} \\ &=& \frac{1}{ \pi } \left\{ – \left[ \frac{1}{n} \sin{nt} \right]_{-\pi}^{0} + \left[ \frac{1}{n} \sin{nt} \right]_{0}^{\pi} \right\} \\ &=& \frac{1}{\pi} (-0+0) \\ &=& 0 \end{eqnarray}

\begin{eqnarray} b_n &=& \frac{1}{ \pi } \left\{ – \int_{-\pi}^{0} \sin{nt} dt + \int_{0}^{\pi} \sin{nt} dt \right\} \\ &=& \frac{1}{ \pi } \left\{ \left[ \frac{1}{n} \cos{nt} \right]_{-\pi}^{0} – \left[ \frac{1}{n} \cos{nt} \right]_{0}^{\pi} \right\} \\ &=& \frac{1}{n \pi} (1 – \cos{n \pi} -( \cos{n \pi} -1 ) ) \\ &=& \frac{2}{ n \pi } (1- (-1)^n ) \end{eqnarray}

\( n \) が奇数のときには \( b_n = 4/ (n \pi) \) となり, nが偶数のときには \( b_n = 0 \) です. よって, 上記方形波のフーリエ級数展開は以下のように表せます.

$$ f(x) = \frac{4}{\pi} \sum_{n=1}^{\infty} \frac{ \sin{(2n-1)x} }{ 2n-1} $$

\( n \) を \( 1 \) から順に足していくと, sin波の重なりが徐々に方形波に収束していく様子が見て取れます.

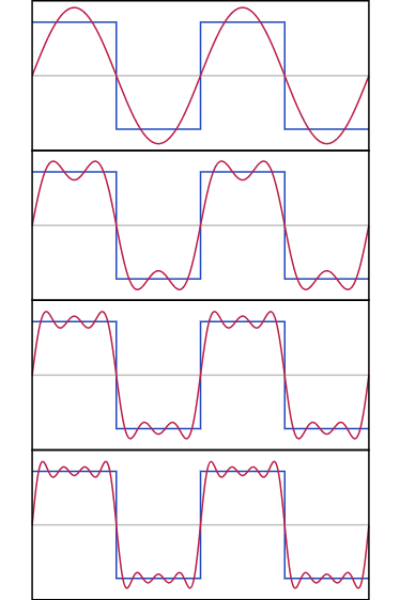
\( n=4 \) まで足した段階でかなり方形波に近い形になりました. このように, フーリエ級数展開を有限項までで止める手法は物理学でもよく用いられる近似手法です.

上記のように, 方形波のフーリエ級数展開における係数を計算すると, 結局 \( a_n \) は消えてなくなり, \( b_n \) のみが残りました. 一般に, 原点を中心として点対称な関数 (今回の方形波のような関数)においては \( a_n \) が消え, y軸対称となる関数 (cos関数のような関数)は \( b_n \) が消えることが知られています.

まとめ

フーリエ級数展開は「とある関数を sin と cos の無限和に変形すること」です.

今のご時世, フーリエ級数の係数の求め方が分からなければ Google先生に聞けば一発で答えてくれます. 頻繁に使うわけではないのなら覚える必要はないでしょう. ただし, フーリエ級数展開が何なのか分からなくなっては, 熱伝導方程式や波動方程式, フーリエ変換, 信号処理などの理解が難しくなります.

今回, フーリエ級数の係数の求め方について, 何の証明もしなかったので次回証明をします. が, これが大変面倒です.

まず,「フーリエ級数展開という概念の理解」こそ重要であると考え, 今回の記事としました. フーリエ級数展開の更なる理解のためには, 次の記事をご参照いただければ幸いです.