コーシーの平均値の定理を視覚的に理解する
オイラーの公式の証明や関数の近似計算をするときに便利なマクローリン展開という操作があります.
今回はマクローリン展開への準備として「コーシーの平均値の定理」をやっていきます.
コーシーの平均値の定理を理解するために重要なことは「図形的イメージ」です。絵を描いて理解しましょう.
Table of Contents
コーシーの平均値の定理の導出

時刻によって位置が変化する点Pが xy平面上を移動するとしましょう.
時刻 \( t \) における点Pの y座標, 及び x座標は以下のように表されることとします.
$$ \left\{ \begin{align} y= \, f(t) \\ x= \, g(t) \end{align} \right. \; \cdots \; (1) $$
点Pが時刻 \( t=a \) において点Aを出発し, 時刻 $ t=b $ において点Bに到着するとします. 点Aから点Bに移動するとき, 点Pがどのような軌跡を描くかは分かりませんが, 以下の図のように移動したとしましょう.
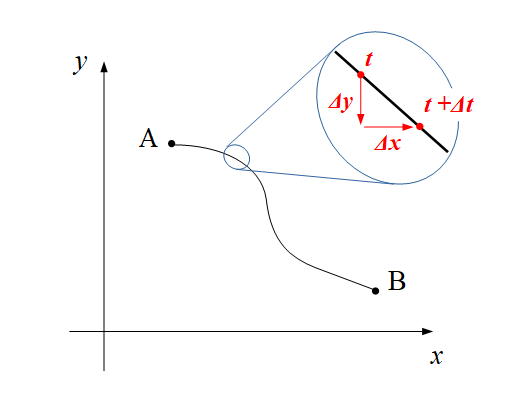
図1の点Pの軌跡について, 接線を考えてみます.
時刻 \( t \) における接線とは, 時刻 \( t \) における点Pの位置 \( (g(t), f(t) ) \) と, 微小時間後 \( t + \Delta t \) における点Pの位置 \( (g \, (t + \Delta t), f \, (t + \Delta t)) \) を結び, \( \Delta t \rightarrow 0 \) の極限を取った直線のことです.
よって, 接線の傾きは
\begin{eqnarray} &\rm{ }& \rm{時刻} \it{t} \rm{ における接線の傾き} = \lim_{t \to 0} \frac{ \left( \it{y} \; \rm{の変化量} \right) }{ \left( \it{x } \; \rm{の変化量} \right) } \\ &=& \lim_{t \to 0} \frac{f(t + \Delta t)-f \, (t)}{g(t + \Delta t)-g \, (t)} = \lim_{t \to 0} \frac{ \left( f \, (t + \Delta t)-f(t) \right) / \Delta t}{ \left( g \, (t + \Delta t)-g(t) \right) / \Delta t} \\ &=& \frac{f'(t)}{g'(t)} \; \cdots \; (2) \end{eqnarray}
となります. 後で大事になるので覚えておいてください.
ここで一旦話は変わり, 点Aと点Bを結ぶ直線の傾きについて考えます.
直線ABの傾きは「変化の割合」, つまり, (yの変化量) / (xの変化量)です.
\begin{eqnarray} &\rm{ }& \rm{直線ABの傾き} \ &=& \frac{f \, (b)-f \, (a)}{g \, (b)-g \, (a)} \; \cdots \; (3) \end{eqnarray}
もう一度, 点Pの描く曲線を眺めてみると, 接線の傾きが直線ABの傾きと同じになる点が存在することが分かります.
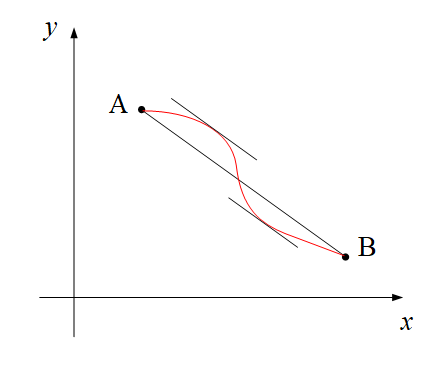
また, 下の図3を見ると, 点Pがいかなる経路を辿ったとしても, 軌跡が滑らかな曲線である限りは, 直線ABの傾き = 接線の傾きとなる点は必ず存在することが分かります.
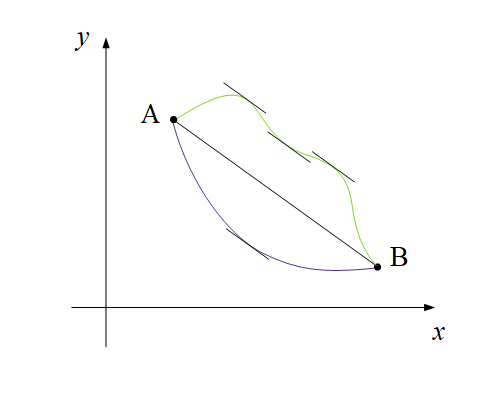
「いかなる経路を辿ったとしても, 直線ABの傾き = 接線の傾きとなる点がAとBの間に存在する」という事実を数式で表したものが, 『コーシーの平均値の定理』です.
ただし, それには条件があり, 地点Aから Bに移動するとき, ワープしたり( \( f \, (t) \) や \( g \, (t) \) が \( t \) に対して非連続), 直角に曲がったり(微分不可能)しないことです.
関数 \( f \, (t) \) と \( g \, (t) \) が \( a \leq t \leq b \) で連続, かつ, \( a < t < b \) で微分可能, さらに \( a < t < b \) で \( g'(t) \neq 0 \) を満たすとき,
$$ \frac{f'(c)}{g'(c)} = \frac{f \, (b)-f \, (a)}{g \, (b)-g \, (a)} \;\;\; (a < c < b) $$
を満たす \( c \) が存在する.
ラグランジュの平均値の定理
コーシーの平均値の定理において \( g(t) = t \) の特殊な場合, \( g'(t)=1 \) となり,
$$ f'(c) = \frac{f \, (b)-f \, (a)}{b-a} \; \cdots \; (4) $$
になります。これをラグランジュの平均値の定理と呼びます。
関数 \( f(t) \) が \( a \leq t \leq b \) で連続かつ, \( a < t < b \) で微分可能のとき,
$$ f'(c) = \frac{f \, (b)-f \, (a)}{b-a} (a < c < b) $$ を満たす \( c \) が存在する.
こちらは高校で習った人もいるかもしれません。
まとめ
コーシーの平均値の定理は数式を眺めるだけでなく, 幾何学的に(図を描いて)考えると理解が容易になる定理の代表です. マクローリン展開の証明に応用されます.
ちなみに, コーシーさんはマクローリン展開の一般形, テイラー展開を考えたテイラーさんより, かなり後の時代の人ですので, コーシーの平均値の定理を使ってテイラー展開が導かれたわけではありません. 歴史的な順序とは異なりますが, 分かりやすさ優先でやっていこうと思います.

