放射束・放射強度・放射輝度とランベルトの余弦則

空洞放射で登場する「ランベルトの余弦則」の話をしようと思ったのですが, 光の強度に関する基本的な物理量（放射強度・放射束・放射輝度）を抑えておいた方が話しやすいなと感じたので, まとめて話すことにしました.

本稿の目的

前回の記事から黒体の話をしています. 高温の黒体から放射される光（黒体放射）の研究は, 量子論が始まるきっかけとなりました.

理想的な黒体はこの世に存在しないため, この研究では小さな穴をあけた空洞を黒体と見立てて放射光に関する研究が行われることとなります. 空洞内部で生じた放射光は壁面に何度もぶつかりつつ吸収され, 空洞内に定常的で等方的な放射場ができるため, 穴から空洞を覗くと黒体放射と全く同じ状況を観測可能です.

では, 実際に空洞内でどのような光の放射場ができているのかを数式に記述していきたいのですが, その前に, 光の強度を表す物理量の基本（放射強度・放射束・放射輝度）と, 理想的な条件における反射光強度の角度依存性（ランベルトの余弦則）について抑えておこうと思います.

心理物理量

蛍光灯やLEDランプの光の明るさを表す際には, 「ルーメン」や「カンデラ」がよく使われます. これらは「光度」や「光束」という物理量の単位です.

しかし, 気を付けねばならないことは, この光度・光束という物理量は平均的なヒトの感覚を基準に定義される物理量（心理物理量）だということです.

ヒトは, 青や赤に比べて緑色の光を強く認識します. 光子の数は同じであっても, 赤や青の光より緑の光の方が「明るい」と感じ, 紫外線や赤外線になると認識することができません. これは視神経の分光感度に依るものです.

光度・光束という物理量はヒト視神経の分光感度を元に波長に重み付けをして算出されます. 当然, 物理学をやるときに使いやすい物理量ではありませんので, 今回は用いません. 以降では, 光度・光束の代わりに, 放射強度・放射束という物理量を用います.

放射強度・放射束

放射束の方から説明します.

放射束はある点光源から放射された光が, ある面を時間当たりに通過するエネルギーを表す物理量です. 光源からある面に対し, 時間当たりにどれだけのエネルギーを受け渡すかを表す量と言っても良いでしょう.

時間当たりのエネルギー移動を表す物理量なので, 単位は [ W（ワット）] です. この面が光源を取り囲んでいる場合, 放射束は光源の仕事率と同じになります.

続いて放射強度です.

放射束の定義で登場した受光面をどんどん小さくしていくと, 光エネルギーの移動は点から点となり, ある一方向へ放射される光強度とみなせます.

この「ある一方向への時間当たりの放射エネルギー」が「放射強度」です.

より詳細には, 放射強度は, 放射束を放射源から見た立体角で微分することで得られます. 単位は仕事率を立体角で割ったものなので, [ W sr^-1（ワット毎ステラジアン）] です.

図と式で見る放射強度・放射束

放射束と放射強度の関係を図を見ながら考えていきます.

下の図では, 放射源から見て位置 \( \boldsymbol{r} \) にある微小面積 \( \Delta S \) が張る立体角を \( \omega ( \Delta S ) \) とし, \( \Delta S \) を貫く放射束を \( \Phi ( \Delta S ) \) としています.

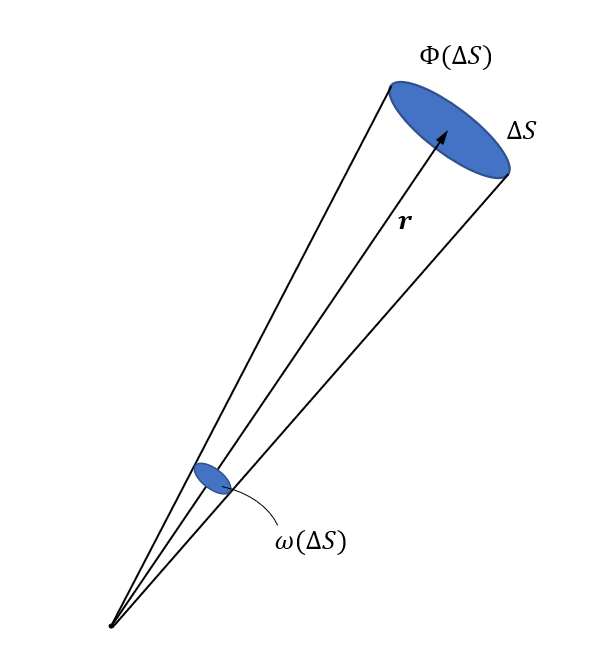
このとき, \( \boldsymbol{r} \) の方向への放射強度は以下で定義されます.

\begin{eqnarray} \boldsymbol{I} = \lim_{ \Delta S \to 0 } \frac{\Phi ( \Delta S )}{\omega ( \Delta S )} = \frac{d \Phi}{d \omega} \;\; \cdots \;\; (1) \end{eqnarray}

放射照度

「ある一方向への放射エネルギー」を定義するときに, 「放射強度」では立体角による微分を使ったわけですが, 面積による微分で考えることもできます. ついでに紹介しておきましょう.

放射束を受光面の面積 \( S \) で微分した

\begin{eqnarray} E=\frac{d \Phi}{d \omega} \;\; \cdots \;\; (2) \end{eqnarray}

を「放射照度」と呼びます.

放射輝度

ここまでの放射束・放射強度・放射照度では光を受け取る側の面積について色々と考えてきましたが, 放射源側の大きさについては特に考えず, 点光源としていました.

しかし, LEDのように面が一様に光を発している場合では 「光源面の面積当たりの明るさ」 を考える必要があります.

このように「光源の放射強度」を「光源面の面積」で割ったものが「放射輝度」です. 放射強度を面積で割るので, 単位は [ W sr^-1 m^-2（ワット毎ステラジアン毎平方メートル）] になります.

より詳細には, 放射輝度は, 放射束を「立体角」と「放射源表面の投影面積」で微分したものとして定義されます. 下図をご覧ください.

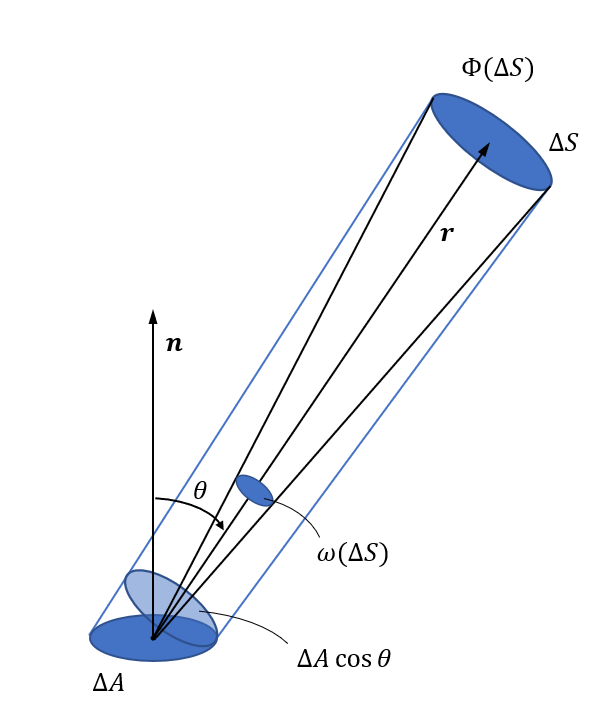
ここで, \( \Delta A \), \( \Delta S \) はそれぞれ光源と受光面の面積です. 受光面は光源上の1点から位置 \( \boldsymbol{r} \) にあります. 光源上の1点から \( \Delta S \) に対して張る立体角を \( \omega ( \Delta S ) \) とすると, \( \Delta A \), \( \Delta S \) が共に十分小さいとき, \( \Delta A \) 上のどの点から見ても \( \Delta S \) に対して張る立体角は同じです.

また, \( \Delta A \) の法ベクトルを \( \boldsymbol{n} \) とし, \( \boldsymbol{n} \) と \( \boldsymbol{r} \) のなす角を \( \theta \) とします.

このとき, 放射輝度は以下のように定義されます.

\begin{eqnarray} L=\lim_{ \Delta A \to 0, \Delta S \to 0 } \frac{\Phi ( \Delta S ) }{ \cos{\theta} \Delta A \omega ( \Delta S ) }=\frac{1}{\cos{\theta}} \, \frac{d^2 \Phi}{dA \, d\omega} \;\; \cdots \;\; (3) \end{eqnarray}

光源の面積に \( \cos{\theta} \) をかけているのは, 光源の面積を「エネルギーが放出される方向に対して垂直な板」に投影しているためです.

人間の目はある点から網膜上の視神経に飛び込んでくる光子の数を「明るさ」として認識しているので, 放射輝度と対応しています. 放射輝度は人間の明るさの感覚と同じようなものと考えて差し支えないでしょう.

ただし, 上述したように人間の視神経は光の波長によって感度が異なり, 放射輝度が同じであったとしても赤色より緑色の方がより明るく感じます. ヒト視神経の分光感度によって補正されたものは単に「輝度」と呼ばれます.

輝度は光束を立体角と光源面積で微分したものです. 物理学に関する本の中でも「光束」や「輝度」が使われることがありますが, 「物理学の本の中に書かれているのだから, 心理物理量の方ではあるまい」と理解すべきでしょう.

ランベルトの余弦則

ここから, ランベルトの余弦則の話をします.

ランベルトの余弦則は, 「ランベルト面における反射光の輝度は角度に依存しない」または「ランベルト面における反射光の放射強度は反射角の余弦に依存する」という法則です.

以下で詳しく説明していきます.

ランベルト面

鏡や磨いた金属の表面では, 「反射角 = 入射角」となる方向へ光の反射が起きます. これを鏡面反射, もしくは正反射と呼びますが, これに対し, 「反射角 ≠ 入射角」である反射を拡散反射と呼びます.

ランベルト面とは, すべての反射光が拡散反射をする面のことです. このランベルト面における反射光の輝度はどの角度から見ても変わらない, というのが「ランベルトの余弦則」です.

また, 放射輝度の定義（ 式(3) ）より, 放射輝度が角度に依存しないということは, 放射強度が反射角の余弦に依存するということでもあります.

微小面積 \( \Delta A \) を角度 \( \theta \) から眺めるというということは, 見かけの面積（投影面積）が \( \Delta A \cos{\theta} \) となっている, ということです. 放射輝度は（放射強度）/（投影面積）で定義されるので, 投影面積が \( \cos{\theta} \) に依存して小さくなっても放射輝度が変わらないということは, 放射強度も \( \cos{\theta} \) に依存して小さくなっている, ということを意味します.

ランベルトの余弦則を図にすると以下のようになります.

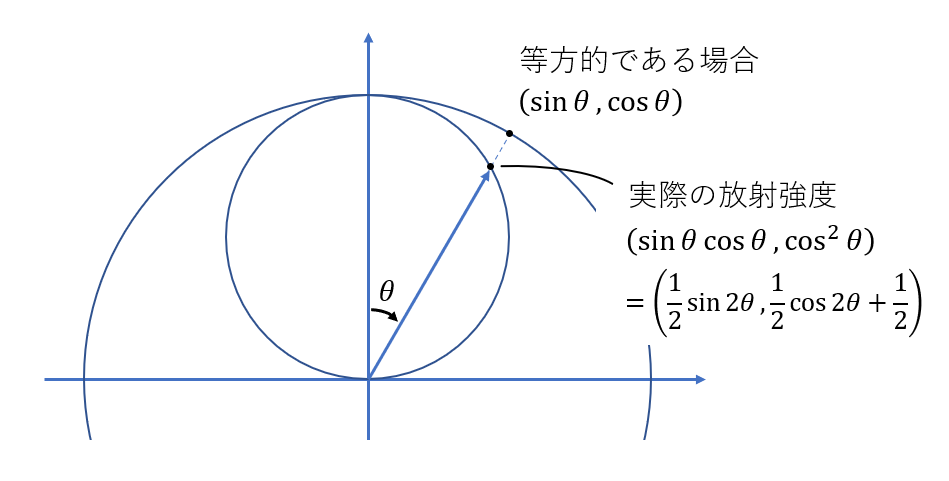
理想的な拡散反射が起きている場合の反射光の放射強度は等方的ではなく, 角度が大きくなると小さくなっていきます. そして, それ故に, 放射輝度は変わりません.

ランベルトの余弦則は, 紙や布など, ツルツルしていない物体表面の多くで近似的に成り立ちます.

例として, 下図の雪をご覧ください. 雪の輪郭付近での反射角はかなり大きくなっていますが, それでも放射輝度が変わっていないことが分かります.

ただし, 厳密に測定すると, 完全なランベルト面は多くなく, ある一方向のへ反射が他の角度より強くなる場合がほとんどです. ランベルトの余弦則は, 拡散反射を強く示す物質の近似値と理解すべきでしょう.

ランベルトの余弦則に関する理論

反射とは, 光によって励起された電子が基底状態に戻る際に起きる光エネルギーの放出です. 空間に原子1個のみが存在するならば, 反射光の放射強度は等方的になるはずです.

なぜ理想的な拡散反射では放射強度が角度の余弦に依存するのでしょうか.

実はこの命題に解析的な答えは存在しません. なぜなら, ランベルトの余弦則は物体の材質や凹凸の影響による統計的帰結だからです. 私個人は「自然界の多くの現象が正規分布で表せる」ということに近いものだと理解しています.

ランベルトの余弦則に関する理論的研究の一端は, 例えば以下のリンクで見ることができます.

拡散反射と表面の光沢I：表面の拡散反射の性質, 蓮沼宏, 応用物理 23巻（1954）.

本引用文献の中では, 光を反射する物質が層状に積み重なったモデルを仮定し, 光の吸収や屈折, 表面の凹凸を加味して反射光の放射強度理論式を導出しています. しかし, 最終的に出てくる理論式が余弦に依存しているわけではありません.

ランベルトの余弦則の応用

物体表面の反射は, 表面の材質や凹凸に依存しています. 逆に言えば, ランベルトの余弦則を使って, 物体表面の材質や凹凸を特定することができる, ということです.

近年では, AIや画像解析による検査技術が急速に発展していますが, ランベルトの余弦則を逆に用いることで, 物体表面の特性を簡易に調べる方法が研究されています.

また, CGなどの視覚効果ではランベルトの余弦則が広く用いられています. CGで作られた美麗なゲームの映像が肉眼で自然に見えるのは, ランベルトの余弦則とヒトの感覚を研究した結果です.

そして, 黒体（空洞放射）の研究もランベルトの余弦則と関係しています.

ランベルト面が実際にはほとんど存在しないことは上述の通りですが, その例外が空洞放射が起きている空洞内部の壁面です. ここでは完全なランベルト面が形成されていることが理論的に導出されます.

次回はその辺りから話を始めたいと思います.

まとめ

ご覧いただきありがとうございました. 本稿内容を雑にまとめます.

1. 放射強度 = 放射束 / 立体角
2. 放射輝度 = 放射強度 / 光源の投影面積
3. ランベルトの余弦則 「理想的な拡散反射面において, 反射光の放射強度は反射角の余弦に依存する」