光の二重性と光電効果
今回から量子についての記事を書いていきます.
第1回は量子論の触りとして, 「光は波なのか, 粒子なのか」を考えていきましょう.
量子論は原子や電子など, 非常に小さな物体を記述しようとする学問ですが, その起源には「光電効果」の発見が深く関わっています. 本稿は, 「光電効果発見以前の光についての認識」, 「光電効果の発見」, 「光量子を用いた光電効果の説明」の順で解説します.
目次
17~18世紀の光についての言説
素元波による波動の解釈で知られるホイヘンス(1629~1695)は光を波だと考えました. 光が波だと考えれば, 障害物を回り込んで光が伝搬する現象(光の回折)を上手く説明できるためです.
これとは対称的に, 古典力学を完成させたニュートン(1643~1727)は「光の粒子説」を主張しました.
光は水面を伝搬する波や音波に比べ, 高い直進性を有しています. 加えて, 光が波ならばその波を伝える媒質が必要となるはずです. しかし, 光は真空中を伝搬します. これこそ, 光が粒子である証拠というわけです.
光の波動説を唱える陣営は, 光の媒質として「エーテル」という未知の物質を仮定します. 透明で, 質量も粘性も零の流体であるエーテルは, 宇宙空間を隙間なく満たしつつも, 天体の運行を妨げることはない, と考えられました.
光の波動説と粒子説は互いに対立しながら, どちらも一定の説得力を有し, 長らく未解決の問題として残り続けることになります.
波動説の証拠1:ヤングの実験
19世紀になってもエーテルは観測されませんでしたが, 光が波動であるという証拠は次第に増えていきました. 代表的なものがヤング(1773~1829)による光の干渉実験です.
二重スリットを介して光を壁面に映し出すと, 特徴的な縞模様が表れます. 光が粒子であり, 光の強度が単なる「粒子の数」であるならばこうはなりません. 特徴的な縞模様は, 光が振幅を持っており他の光と強め合ったり弱め合ったりする現象, 即ち「波の干渉」を起こしている強力な証拠となります.
波動説の証拠2:マクスウェルの電磁波に関する予言
光の波動説に関する次なる証言者はマクスウェル(1831~1879)です. 彼は電気と磁気に関する4つの方程式をマクスウェル方程式としてまとめたことで知られます. 電磁気学はこの功績によって確立されました.
マクスウェルは, 真空中(つまり電荷も電流も存在しない空間)で時間的に変化する電場と磁場を仮定すると, 電場と磁場が互いに直交しつつ振動する波動方程式が導かれることを示しました. マクスウェルはこのような波(電磁波)が現実に存在することを自身の論文中で予言します.
また, マクスウェルは, 導出された電磁波の速度が当時実際に観測されていた光の速度とおおよそ一致することから, 光は電磁波であると主張しました.
電磁波に関するマクスウェルの予言は, マクスウェルの死後, ヘルツ(1857~1894)の行った実験によって証明され, 「光=電磁波」が科学界において一定の支持を得ることになります.
光電効果の発見
光=電磁波が確からしいと広く信じられるようになり, この問題に決着が訪れたと思ったのも束の間. 光の波動説を揺るがす実験事実が観測されました. それがレーナルトによる「光電効果」の実験です.
光電効果とは, 「金属に光を照射すると電子が飛び出す」という現象を指します. 1839年に光起電力について調べていたベクレル(1820~1891)が発見しました.
これを電磁気学的に解釈するならば, 「電磁波が金属原子の軌道上に存在する電子にエネルギーを与え, 電子を束縛するエネルギーを上回ったときに電子が飛び出す現象」ということになります.
これならば, 特段電磁気学と矛盾するところはありません. しかし, その後レーナルト(1862~1947)が光電効果を詳しく調べる中で, 古典物理学だけでは説明できない性質が見つかってきます.
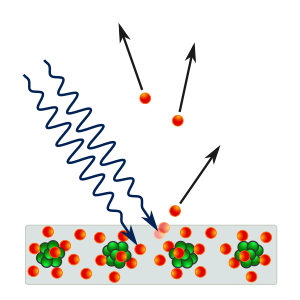
光電効果に関する詳細な実験
レーナルトは照射する光の強度や波長, 照射時間などを色々と変えつつ, 飛び出してくる電子(光電子)の運動エネルギーや数を観測し, 以下のような結果を得ました.
- 電子の放出は, ある一定以上の振動数(一定以下の波長)の光でしか起きず, それ以下の振動数の光を長時間照射しても光電子は観測されない.
- 振動数の大きな光を当てると光電子の運動エネルギーは増大するが, 光電子の数に変化はない.
- 光の強度を上げると光電子の数が増えるが, 電子1個の運動エネルギーに変化はない.
これのどこに古典力学との矛盾があるのでしょうか?
矛盾
高校物理では, 最初の方でばねの単振動を習いますが, ばねに取り付けられた重りが持つ力学的エネルギー \(E\)(位置エネルギー+運動エネルギー)は以下の形で表されるのでした.
\begin{eqnarray} E=\frac{1}{2}kA^2 \end{eqnarray}
ここで, \(k\) はばね定数, \(A\) は振幅を表しますが, ばね定数は \(k=m \omega ^2\)(\(m\):重りの質量, \(\omega\):角振動数)なので, 結局, 重りが持つエネルギーは振幅の2乗と振動数の2乗にそれぞれ比例します.
弦を伝わる振動であっても基本的な形は同じで, このエネルギーが伝搬していきます.
古典力学では, 光からエネルギーを受け取って, エネルギーが増大した電子が飛び出す, と考えました. つまり, 光が波ならば, 電子の放出には振動数と振幅(つまり光の強度)の双方が寄与するはずです.
確かに, 振動数も振幅も光電効果における電子の放出に寄与しています. しかし, レーナルトの調べた結果によると, 振動数と振幅が光電効果に及ぼす影響は一様ではありませんでした.
振幅(つまり光の強度)を大きくしていけば波としてのエネルギーは大きくなるはずです. しかし, ある一定以下の振動数の光では, どんなに強度を大きくして, どれだけ長時間光を照射しても電子は飛び出しません. この性質は, それまでの物理学では説明できないものでした.
困惑
レーナルトの実験結果が確からしい, ということになってくると光について色々と考え直す必要があります.
そもそも, 電場と磁場を直交させつつ前進する, という特殊な形状と特殊な媒質(この頃まだエーテルの存在は広く信じられていました)を持つのが「光」です. 振幅, 振動数, エネルギーの関係についても特殊な関係性を持つのかもしれません.
それとも, 光を受け取る側の金属について考え違いをしているのでしょうか?金属は原子の規則的な配置で出来た結晶で, 原子は電子と原子核で出来ていることは分かっています. 例えば, 光の強度の影響を減衰させ, 振動数のみからエネルギーを受け取る構造があると考えることもできます.
「光は電子放出にのみ寄与し, 放出された電子の運動エネルギーは金属の熱から受け取っているのでは?」という仮説もありました. しかし, この仮説で説明できるのは, 「光の強度が電子の運動エネルギーに寄与しない」という点のみです. 後の検証実験では, 光電効果と金属温度に強い相関がないことも分かっています.
いよいよ回答に窮した学者たちはどうしたかというと, この問題について一旦棚上げすることにしました.
この問題への回答はレーナルトの発表からそれほど時をおかずに提示されましたが, それは, 光を研究する者たちにとって好ましい回答ではありませんでした.
光量子仮説
1905年, 日本がロシアと海戦を繰り広げていた只中, 先に登場したレーナルトは陰極線(真空放電により生じる電子の流れ)に関する研究でノーベル賞を受賞しました.
同時に, 1905年は「アインシュタインの奇跡の年」と呼ばれます. アインシュタイン(1879~1955)が発表した3つの論文は, 後の物理学を, 文字通り根底から覆すものでした.
1つ目の論文(※1)は, 「ブラウン運動」を説明したものです. 原子の存在に関して, 当時まだまだ否定的な意見が多く存在しましたが, この論文によって原子の存在をより確固たるものにしました.
2つ目は, 「相対性理論」に関する論文です. 光速度が常に一定である実験事実を説明するため, 「速く動くと時間の流れが遅くなる」という無茶苦茶なことを言い出しました. 私たちの経験や感覚と酷く乖離したこの理論は, その後多くの批判に晒されます.
そして3つ目が, 「光電効果」に関する論文でした. アインシュタインは, この論文中で, 光電効果という難問を見事に説明してみせます.
(※1)話の流れ上, 光電効果を最後に持ってきたが, 実際の順番は「光電効果(3月)」→「ブラウン運動(5月)」→「相対性理論(6月)」
粒子論の復権
アインシュタインは, 100年も前に失われた「光の粒子説」を引っ張り出し, 以下のような説明をしました.
曰く, 「光電現象は, 空中を動き回るボールを狙う射的のようなものだ. 光という弾丸がボールに命中すると, ボールは弾き飛ばされて金属から放出される. しかし, 弾に威力がなければ, いくら弾を撃っても, ボールを弾き飛ばすことができない.」
このように考えれば, 光電効果における光の振動数と強度, 及び, 光電子のエネルギーと数についての関係を見事説明することができます. 問題は, 「光が粒子だとすると, 過去の偉人達が示した光の波動性に関する証拠をどう説明するのか」ということです.
これに対してアインシュタインは「光は『波』としての性質と, 『粒子』としての性質を併せ持つ『量子』である」と主張します. これは, 当時プランク(1858~1947)らが発見したエネルギーの量子化から着想を得ています.
古典力学では連続的な量だと考えられていたエネルギーに, それ以上分割できない最低単位(量子)が存在すること. それは, 光にも当てはまるのではないか, と考えたのです.
反発
「光は波であり, 粒子でもある」
それは私たちの頭でイメージすることができません. つまり, 絵として描くことができません.
観察と実験を是とする物理学では, 常に私たちの身体感覚が重視されました. 目に見えない音波やミクロな物体の挙動であっても, 絵として描くことで日常の風景と結びつけることができます.
原子の惑星モデルが広く受け入れられたのは, 電子の回転によって磁気が生じるという理論との一致だけでなく, そのモデルが美しかったためでもあるでしょう. 歯車や渦, 竜巻, 太陽の周りを周回する惑星のように, 自然界, 人間界には回転して安定する物体が多く存在します. あらゆる法則は, ミクロな世界でも同じく成り立ち, 全ては繋がっていると「体感」するときに, 物理現象をはじめて理解することができるのです.
しかし, 「波であり, 粒子でもある」物体など, 私たちは他に知りません. 「光量子」という概念は新しいというだけでなく, 従来の物理学にない「生理的な気持ち悪さ」があったのでしょう.
レーナルトの光電効果に関する論文を呼んだアインシュタインは, そこから着想を得て「光量子」に至ります. 素晴らしい結果を示してくれたレーナルトに対して, アインシュタインは感謝と畏敬の手紙を送りました. 当初懇意にしていた両者ですが, 光量子に関するレーナルトの忌避感と, 相対論をめぐる意見の対立, ドイツ民族主義の高まりも相まって, 両者の関係は決定的に壊れてしまいます.
量子という存在は, それほどまでに受け入れがたく, 従来の物理学と一線を画した存在だったのです.
量子によって意味付けられる世界
量子を忌避し, 従来の物理学的枠組みを延長することで現象を説明しようとする勢力に対し, 量子論陣営は次々にその理論的正しさを証明していきました.
特に蛍光, 比熱, 光化学などに関しては, 光電効果と同じように, 従来無視されていた不可解な現象の説明に量子論が大きな役割を果たしていきます. どうやら, 物理学とは, 不都合なものは極力見ないようにする習わしがあったようです.
量子論は一日にして世界に受け入れられたのではありません. 量子論を用いれば説明できる現象が増えるにつれ, その有用性を認めざるを得なかったというのが本当のところでしょう.
まとめ
最後までご覧いただきありがとうございます.
以下では, 本稿執筆にあたって参考にした書籍を示します.
- 「アインシュタインとヒトラーの科学者: ノーベル賞学者レーナルトはなぜナチスと行動を共にしたのか」Bruce J. Hillman 著, 原書房
- 「量子論の生いたち」 Banesh Hoffmann 著, 河出書房新社
- 「物理の歴史」朝永振一郎著, 筑摩書房

