n端子対回路網の行列表現とZ行列・F行列・S行列の相互変換
入力端子対や出力端子対が複数存在する回路の解析において役立つのが, n端子対回路という考え方です.
本稿では n端子対回路網における Z行列, S行列, F行列の導出と, n端子対回路網における縦続接続の方法について解説していきます.
Table of Contents
n端子対回路とは
n端子対回路とは 2端子対回路という考え方を拡張した概念です.
以下では, 2端子対回路の復習から始めて, n端子対回路を導出していきます.
2端子対回路
2端子対回路について復習していきましょう.
「端子(terminal)」とは回路上のとある 1点のことです. また, 「端子対(port)」とは 「2つの端子のペア」を指しますが, 「流れる電流の大きさが同じで向きが逆」という条件を常に満たします.
電源プラグからは 2本の金属端子が出ていますが, あの金属端子のペアは端子対になっています.
2端子対回路網の例として「扇風機」を考えます. 簡単のために首振り機能やタイマー機能の付いていないものを考えましょう.
扇風機とは電力を運動エネルギーに変換する装置です. 家庭用コンセントから電力を受け取り, モーターで電力を消費します.
このコンセントに挿入されたプラグを「入力端子対」と考え, モーター両端の 2点を「出力端子対」とします. このとき, 入力端子対の各端子には同じ大きさの電流が逆向きに流れていて, これは出力端子対においても同様です.
こうして入力端子対と出力端子対を設定すると, 2つの端子対に囲まれ, 電気的に他と隔絶された領域が出来上がります. この領域が 2端子対回路網です.
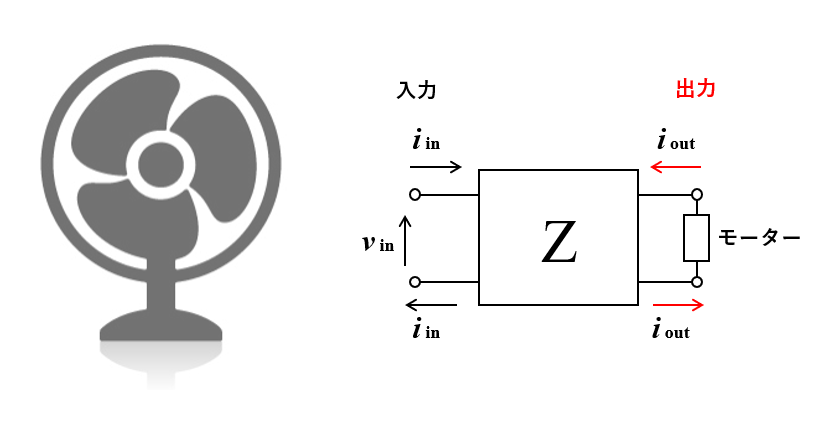
2端子対回路という概念が優れているのは「扇風機を分解せずに, 扇風機の電気的特性を解析できる」という点です.
2端子対回路網に電圧を印加し, 流れる電流を観測すると, 以下のように, 電圧 – 電流の関係を表す式を導出できます.
\begin{eqnarray} \left[ \begin{array}{cc} \, \dot{V}_{in} \\ \, \dot{V}_{out} \end{array} \right] = \left[ \begin{array}{rr} \dot{Z}_{11} & \dot{Z}_{12} \\ \dot{Z}_{21} & \dot{Z}_{22} \end{array} \right] \, \left[ \begin{array}{cc} \, \dot{I}_{in} \\ \, \dot{I}_{out} \end{array} \right] \; \cdots \; (1) \end{eqnarray}
電圧と電流を関係付ける, この \(2 \times 2\) の行列 \(Z = \left[ \begin{array}{rr} \dot{Z}_{11} & \dot{Z}_{12} \\ \dot{Z}_{21} & \dot{Z}_{22} \end{array} \right]\) がインピーダンス行列(Z行列)です.
Z行列が分かっている回路においては, 入力電圧・電流から, 出力電圧・電流を計算できます. 逆もまた然り.
つまり, 回路をばらして, 回路を構成する部品を眺めずとも, その回路の電気的特性全てが既知となるのです.
注意すべき点として, 上記のように 2端子対回路網で全てを記述できるのは「回路網が線形素子のみで構成されている場合」に限定されます. 線形素子とは, 印加される電圧と流れる電流が比例関係になる素子であり, 純抵抗やコイル, キャパシタなどのことです.
2端子対回路について詳しくは以下のリンクをご参照下さい.
n端子回路網への拡張
2端子対回路網では「扇風機」を例に挙げました. 扇風機は「コンセント」から電力を得, 「モーター」で電力を消費します. 入力端子対 1つ, 出力端子対も 1つです.
対して「ドライヤー」という装置は, 電力を「風」に変えるモーターと, 「熱」に変える電熱線という 2つの出力を持ちます.
入力 1つ, 出力 2つの 3端子対を持つわけです. 2端子対回路網のままではドライヤーを扱うことはできません. 2端子対回路網の考え方を拡張し, 3端子対以上の場合を考える必要があります.
3端子対以上の回路網とは, すなわち以下のような回路網です.
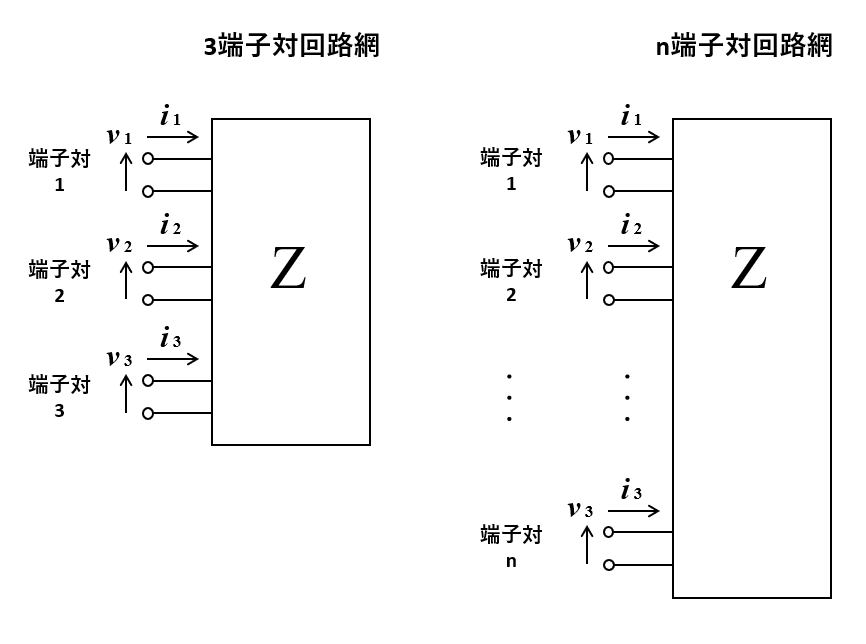
3端子対回路網の場合, 電流, 電圧と Z行列が以下のような関係になります.
\begin{eqnarray} \left[ \begin{array}{cc} \, \dot{V}_{1} \\ \, \dot{V}_{2} \\ \, \dot{V}_{3} \end{array} \right] = \left[ \begin{array}{rrr} \dot{Z}_{11} & \dot{Z}_{12} & \dot{Z}_{13} \\ \dot{Z}_{21} & \dot{Z}_{22} & \dot{Z}_{23} \\ \dot{Z}_{31} & \dot{Z}_{32} & \dot{Z}_{33} \end{array} \right] \, \left[ \begin{array}{cc} \, \dot{I}_{1} \\ \, \dot{I}_{2} \\ \, \dot{I}_{3} \end{array} \right] \; \cdots \; (2) \end{eqnarray}
同様に, n端子対回路網の場合は以下のように定義できます.
\begin{eqnarray} \left[ \begin{array}{cc} \, \dot{V}_{1} \\ \, \dot{V}_{2} \\ \, \vdots \\ \, \dot{V}_{n} \end{array} \right] = \left[ \begin{array}{cccc} \dot{Z}_{11} & \dot{Z}_{12} & \ldots & \dot{Z}_{1n} \\ \dot{Z}_{21} & \dot{Z}_{22} & \ldots & \dot{Z}_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ \dot{Z}_{n1} & \dot{Z}_{n2} & \ldots & \dot{Z}_{mn} \end{array} \right] \, \left[ \begin{array}{cc} \, \dot{I}_{1} \\ \, \dot{I}_{2} \\ \, \vdots \\ \, \dot{I}_{n} \end{array} \right] \; \cdots \; (3) \end{eqnarray}
こうして Z行列が定められるのは, 回路が線形性を持つためです.
n端子対回路網における Z行列の求め方
ここからは n端子対回路網における Z行列の導出方法について解説します.
各端子対には \( m = 1\) ~ \(n \) と番号を付けておき, Z行列の上の行の成分から順に求めていきましょう.
式(3) より, 端子対 \(m=1\) における電圧と, 各端子対を流れる電流とは以下の関係があります.
$$ \dot{V}_{1} \, = \, \dot{Z}_{11} \, \dot{I}_{1} \, + \, \dot{Z}_{12} \, \dot{I}_{2} \, + \, \cdots \, + \, \dot{Z}_{1n} \, \dot{I}_{n} \; \cdots \; (4) $$
n個ある端子対のうちの \(m=2\) ~ \(n\) の端子対を開放(\( \dot{I}_{m \neq 1} = 0 \)), \(m=1\) に一定の電圧 \( \dot{V}_{1a} \) を印加し, そのとき \(m=1\) において流れる電流が \( \dot{I}_{1a} \) だったとすると, 以下の関係が導かれます.
$$ \dot{V}_{1a} \, = \, \dot{Z}_{11} \, \dot{I}_{1a} \; \cdots \; (5) $$
よって,
$$ \dot{Z}_{11} \, = \, \frac{ \dot{V}_{1a} }{ \dot{I}_{1a} } \; \cdots \; (6) $$
\(\dot{Z}_{11}\) が求められました.
式(5) と式(6) における \( \dot{V}_{1a} \), \( \dot{I}_{1a} \) は端子対 \(m=1\) に印加する電圧の大きさで変わってきますが, その比である \( \dot{Z}_{11} \) は一定です.
続いて, \(m=2\) 以外の端子対を開放(\( \dot{I}_{m \neq 2} = 0 \)), 端子対 \(m=1\) に一定の電圧 \( \dot{V}_{1b} \) を印加し, このとき端子対 \(m=2\) に流れる電流が \( \dot{I}_{2b} \) だとすると, 式(4) より, 以下の関係が導かれます.
$$ \dot{V}_{1b} \, = \, \dot{Z}_{12} \, \dot{I}_{2b} \; \cdots \; (7)$$
ここから \( \dot{Z}_{12} \) が分かります. 以下同様です.
これを他の行でも同じようにやっていけば, すべての行列要素を求められます.
S行列, F行列への変換
2端子対回路網において, 回路の行列表現は 1通りではありませんでした. 特に F行列は回路の縦続接続を考えるときに大変便利です.
S行列や F行列は本質的に Z行列と同じものを表しています. Z行列が求められるのならば, S行列や F行列も求められるはずです.
Z行列⇔S行列変換
回路網に対する電力の入射と反射を表現する行列が S行列です. Z行列と違って, 交流信号のみに適用できます(Z行列は直流も交流も扱える).
2端子対回路網における S行列は以下の形で表されるのでした.
\begin{eqnarray} \left[ \begin{array} \, \dot{b}_1 \\ \dot{b}_2 \end{array} \right] \, = \, \left[ \begin{array}{cc} \, \dot{S}_{11} & \dot{S}_{12} \\ \, \dot{S}_{21} & \dot{S}_{22} \end{array} \right] \, \left[ \begin{array} \, \dot{a}_1 \\ \dot{a}_2 \end{array} \right] \; \cdots \; (8) \end{eqnarray}
ここで, \(\dot{a}_{1}\), \(\dot{a}_{2}\) や \(\dot{b}_{1}\), \(\dot{b}_{2}\) は 各端子対における回路網への入射波, または回路網からの反射波を表しています. 入射波と反射波を関係付ける行列 \( S= \, \left[ \begin{array}{cc} \, \dot{S}_{11} & \dot{S}_{12} \\ \, \dot{S}_{21} & \dot{S}_{22} \end{array} \right] \) が S行列です.
S行列について詳しくは以下のリンクをご参照下さい.
S行列と Z行列は以下の関係にあります.
$$ Z = U \, \left( E \, – \, S \right) ^{-1} \, \left( E \, + \, S \right) \, U \; \cdots \; (9) $$
2端子対回路網において, \(E\) は \(2 \times 2\) の単位行列で, \(U= \, \left[ \begin{array}{cc} \, \sqrt{ \dot{z}_1 } & 0 \\ \, 0 & \sqrt{ \dot{z}_2 } \end{array} \right]\), \(\dot{z}_1\) と \(\dot{z}_2\) はそれぞれ端子対 1, 2 における特性インピーダンスです.
この関係は n端子対回路網でも変わりません. 式(9) の関係式に n端子対回路網の Z行列の式を放り込むと, S行列ができます.
ただし, n端子対回路網では \(E\) と \(U\) は \(n \times n\) の対角行列になります.
n端子対回路網 F行列の導出
S行列は容易に導出されましたが, F行列に変換するのは少々大変です.
n端子対回路網における F行列を求めるためには, F行列の役割から考える必要があります.
そもそも F行列とは縦続接続を容易にするためのものでした. 縦続接続とは, 下図のように回路を接続し, 1つの回路網に変換する操作です.
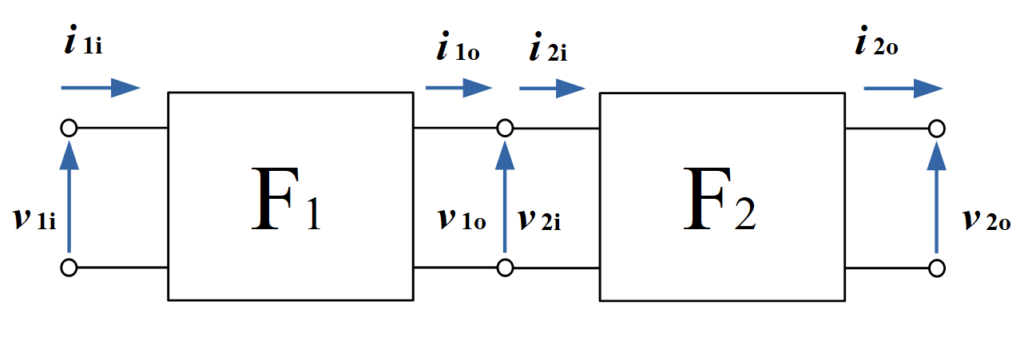
図3 は2端子対回路網同士の縦続接続です. n端子対回路網に拡張するならば, 以下の図4のような縦続接続となるでしょう.
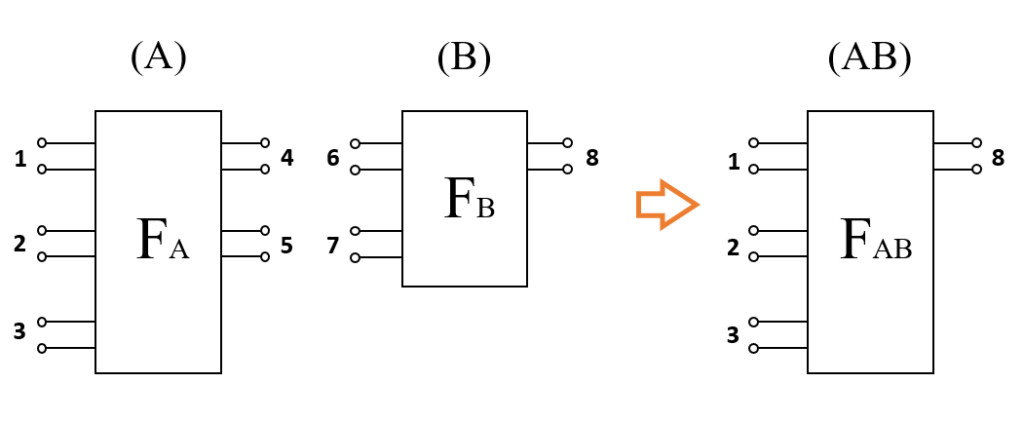
この縦続接続を考えるために必要な行列が F行列です.
F行列には便宜上(定義上), 「入力端子対」と「出力端子対」が必要になります. 「どこを入力端子対と出力端子対にするか」は自分で決めねばなりません.
図4 (A) の 回路網において, 端子対 1, 2, 3 を入力端子対, 端子対 4, 5 を出力端子対とすれば, F行列は
\begin{eqnarray} \left[ \begin{array} \, \dot{V}_{1} \\ \dot{I}_{1} \\ \dot{V}_{2} \\ \dot{I}_{2} \\ \dot{V}_{3} \\ \dot{I}_{3} \end{array} \right] \, = \, \left[ \begin{array}{cccccc} \, \dot{F}_{v1v4} & \dot{F}_{v1i4} & \dot{F}_{v1v5} & \dot{F}_{v1i5} \\ \dot{F}_{i1v4} & \dot{F}_{i11i4} & \dot{F}_{i1v5} & \dot{F}_{i1i5} \\ \dot{F}_{v2v4} & \dot{F}_{v2i4} & \dot{F}_{v2v5} & \dot{F}_{v2i5} \\ \dot{F}_{i2v4} & \dot{F}_{i2i4} & \dot{F}_{i2v5} & \dot{F}_{i2i5} \\ \dot{F}_{v3v4} & \dot{F}_{v3i4} & \dot{F}_{v3v5} & \dot{F}_{v3i5} \\ \dot{F}_{i3v4} & \dot{F}_{i3i4} & \dot{F}_{i3v5} & \dot{F}_{i3i5} \end{array} \right] \, \left[ \begin{array} \, \dot{V}_{4} \\ \dot{I}_{4} \\ \dot{V}_{5} \\ \dot{I}_{5} \end{array} \right] \; \cdots \; (10) \end{eqnarray}
と表せます. 一方で, 同じ図4 (A) の回路網であっても, 端子対 1 を入力端子対, 他を出力端子対とすれば, F行列は以下の形になります.
\begin{eqnarray} \left[ \begin{array} \, \dot{V}_{1} \\ \dot{I}_{1} \end{array} \right] \, = \, \left[ \begin{array}{cccccc} \, \dot{F}_{v1v2} & \dot{F}_{v1i2} & \dot{F}_{v1v3} & \dot{F}_{v1i3} & \dot{F}_{v1v4} & \dot{F}_{v1i4} & \dot{F}_{v1v5} & \dot{F}_{v1i5} \\ \dot{F}_{i1v2} & \dot{F}_{i1i2} & \dot{F}_{i1v3} & \dot{F}_{i1i3} & \dot{F}_{i1v4} & \dot{F}_{i1i4} & \dot{F}_{i1v5} & \dot{F}_{i1i5} \end{array} \right] \, \left[ \begin{array} \, \dot{V}_{2} \\ \dot{I}_{2} \\ \dot{V}_{3} \\ \dot{I}_{3} \\ \dot{V}_{4} \\ \dot{I}_{4} \\ \dot{V}_{5} \\ \dot{I}_{5} \end{array} \right] \; \cdots \; (11) \end{eqnarray}
同じ回路網を扱っていても, 自分で勝手に決めた入力端子対と出力端子対によって F行列の形は変わってしまうのです.
また, 入力端子対と出力端子対で電流の向きが異なることも注意が必要となります. \(\dot{I}_2\) と \(\dot{I}_3\) は 式(10) と 式(11) で電流の向きが反対になっています.
Z行列から任意の F行列を導出する一般的な方法は存在しますが, Z⇔F変換の一般式は煩雑で, 使い勝手が良いとは言い難いかと.
F行列は力技で導出するのが良いでしょう(端子対が増えてきた場合には当然ながらその限りではありません).
一例として, 図4 (A) の5端子対回路網についてF行列を求めてみます.
例:5端子対回路網における F行列
図4 (A) において, 入力端子対に \(m=1, 2, 3\)を取り, 出力端子対に \(m=4, 5\) を取ったとき, 電流・電圧の関係は式(10) に示した通りです.
\begin{eqnarray} \left[ \begin{array} \, \dot{V}_{1} \\ \dot{I}_{1} \\ \dot{V}_{2} \\ \dot{I}_{2} \\ \dot{V}_{3} \\ \dot{I}_{3} \end{array} \right] \, = \, \left[ \begin{array}{cccccc} \, \dot{F}_{v1v4} & \dot{F}_{v1i4} & \dot{F}_{v1v5} & \dot{F}_{v1i5} \\ \dot{F}_{i1v4} & \dot{F}_{i1i4} & \dot{F}_{i1v5} & \dot{F}_{i1i5} \\ \dot{F}_{v2v4} & \dot{F}_{v2i4} & \dot{F}_{v2v5} & \dot{F}_{v2i5} \\ \dot{F}_{i2v4} & \dot{F}_{i2i4} & \dot{F}_{i2v5} & \dot{F}_{i2i5} \\ \dot{F}_{v3v4} & \dot{F}_{v3i4} & \dot{F}_{v3v5} & \dot{F}_{v3i5} \\ \dot{F}_{i3v4} & \dot{F}_{i3i4} & \dot{F}_{i3v5} & \dot{F}_{i3i5} \end{array} \right] \, \left[ \begin{array} \, \dot{V}_{4} \\ \dot{I}_{4} \\ \dot{V}_{5} \\ \dot{I}_{5} \end{array} \right] \; \cdots \; (10) \end{eqnarray}
ここで, 入出力端子対の電流・電圧を関係付ける \(4 \times 6\) の行列が F行列です. F行列の成分を求めていきましょう. やることは, Z行列導出のときにやったことと変わりません.
まず, 式(10) の \( \dot{V}_{1} \) に関する式を取り出して見てみます.
\begin{eqnarray} \dot{V}_{1} \, = \, \dot{F}_{v1v4} \, \dot{V}_{4} \, + \, \dot{F}_{v1i4} \, \dot{I}_{4} \, + \, \dot{F}_{v1v5} \, \dot{V}_{5} \, + \, \dot{F}_{v1i5} \, \dot{I}_{5} \; \cdots \; (12) \end{eqnarray}
ここで, \(m=4, 5\) の端子対を開放, \(m=1\) の端子対に定電圧 \(\dot{V}_{1a}\) を印加して, \(m=4, 5\) の端子対における電圧を測定します. \(m=4, 5\) において, 測定された電圧がそれぞれ \(\dot{V}_{4a}\), \(\dot{V}_{5a}\) だったとすると, 各端子対における電圧の関係は以下のように表されます.
\begin{eqnarray} \dot{V}_{1a} = \dot{F}_{v1v4} \, \dot{V}_{4a} + \dot{F}_{v1v5} \, \dot{V}_{5a} \; \cdots \; (13) \end{eqnarray}
同様に, \(m=4, 5\) の端子対を開放し, 今度は \(m=1\) の端子対に定電圧 \(\dot{V}_{1b}\) を印加して, \(m= 4, 5\) の端子対における電圧を測定します. 測定された電圧がそれぞれ \(\dot{V}_{4b}\), \(\dot{V}_{5b}\) だったとすると,
\begin{eqnarray} \dot{V}_{1b}= \dot{F}_{v1v4} \, \dot{V}_{4b} + \dot{F}_{v1v5} \, \dot{V}_{5b} \; \cdots \; (14) \end{eqnarray}
式(13), (14) は \(\dot{F}_{v1v4}\) と \(\dot{F}_{v1v5}\) についての連立方程式であり, これを解くと, \(\dot{F}_{v1v4}\) と \(\dot{F}_{v1v5}\) が求められます.
端子対 \(m=4, 5\) を短絡させて同様の測定を行えば, \(\dot{F}_{v1i4}\) と \(\dot{F}_{v1i5}\) を算出することが可能です.
また, ここまでの測定では端子対 \(m=1\) に定電圧を印加してきましたが, 端子対 \(m=1\) に定電流を印加して同様の測定をすれば, \(\dot{F}_{i1v4}\), \(\dot{F}_{i11i4}\), \(\dot{F}_{i1v5}\), \(\dot{F}_{i1i5}\) が求めらます.
定電圧を印加する端子対を変え, \(m=2, 3\) の場合も同様に測定を行えば, すべての行列要素を求めることが可能です.
n端子回路網の縦続接続
上述の通り, F行列は回路の縦続接続をサポートするツールです. 実際に以下の図のような縦続接続を考えてみます.
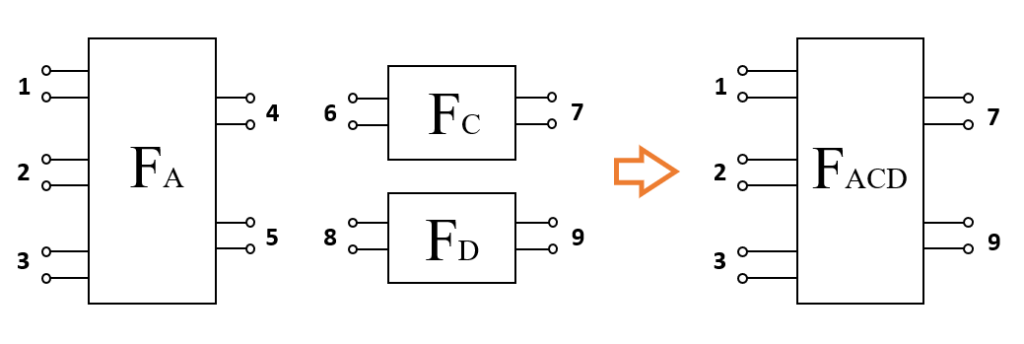
端子対 4 と 6 を接続し, 5 と 8 も接続します.
各F行列は
\(F_{A} = \left[ \begin{array}{cccccc} \, \dot{F}_{v1v4} & \dot{F}_{v1i4} & \dot{F}_{v1v5} & \dot{F}_{v1i5} \\ \dot{F}_{i1v4} & \dot{F}_{i11i4} & \dot{F}_{i1v5} & \dot{F}_{i1i5} \\ \dot{F}_{v2v4} & \dot{F}_{v2i4} & \dot{F}_{v2v5} & \dot{F}_{v2i5} \\ \dot{F}_{i2v4} & \dot{F}_{i2i4} & \dot{F}_{i2v5} & \dot{F}_{i2i5} \\ \dot{F}_{v3v4} & \dot{F}_{v3i4} & \dot{F}_{v3v5} & \dot{F}_{v3i5} \\ \dot{F}_{i3v4} & \dot{F}_{i3i4} & \dot{F}_{i3v5} & \dot{F}_{i3i5} \end{array} \right]\), \(F_{C} = \left[ \begin{array}{cc} \, \dot{F}_{v6v7} & \dot{F}_{v6i7} \\ \dot{F}_{i6v7} & \dot{F}_{i6i7} \end{array} \right] \), \(F_{D} = \left[ \begin{array}{cc} \, \dot{F}_{v8v9} & \dot{F}_{v8i9} \\ \dot{F}_{i8v9} & \dot{F}_{i8i9} \end{array} \right] \)
です.
F行列を使って縦続接続をするためには,
\begin{eqnarray} \left[ \begin{array} \, \dot{V}_{6} \\ \dot{I}_{6} \\ \dot{V}_{8} \\ \dot{I}_{8} \end{array} \right] \, = \, \left[ \begin{array}{cccc} \, \dot{F}_{v6v7} & \dot{F}_{v6i7} & \dot{F}_{v6v9} & \dot{F}_{v6i9} \\ \dot{F}_{i6v7} & \dot{F}_{i6i7} & \dot{F}_{i6v9} & \dot{F}_{i6i9} \\ \dot{F}_{v8v7} & \dot{F}_{v8i7} & \dot{F}_{v8v9} & \dot{F}_{v8i9} \\ \dot{F}_{i8v7} & \dot{F}_{i8i7} & \dot{F}_{i8v9} & \dot{F}_{i8i9} \end{array} \right] \, \left[ \begin{array} \, \dot{V}_{7} \\ \dot{I}_{7} \\ \dot{V}_{9} \\ \dot{I}_{9} \end{array} \right] \; \cdots \; (15) \end{eqnarray}
という行列が必要です.
図5を見ると, 端子対 \(m=6\) と 端子対 \(m=9\) は接続されておらず, 一切の相互作用がありません. つまり, 端子対 \(m=6\) と \(m=9\) の関係を表す成分 \(\dot{F}_{v6v9}\), \(\dot{F}_{v6i9}\), \(\dot{F}_{i6v9}\), \(\dot{F}_{i6i9}\) は \(0\) になります.
端子対 \(m=8\) と \(m=7\) の関係を表す行列成分も同様に \(0\) です.
よって, 式(15) は以下のように書き換えられます.
\begin{eqnarray} \left[ \begin{array} \, \dot{V}_{6} \\ \dot{I}_{6} \\ \dot{V}_{8} \\ \dot{I}_{8} \end{array} \right] \, = \, \left[ \begin{array}{cccc} \, \dot{F}_{v6v7} & \dot{F}_{v6i7} & 0 & 0 \\ \dot{F}_{i6v7} & \dot{F}_{i6i7} & 0 & 0 \\ 0 & 0 & \dot{F}_{v8v9} & \dot{F}_{v8i9} \\ 0 & 0 & \dot{F}_{i8v9} & \dot{F}_{i8i9} \end{array} \right] \, \left[ \begin{array} \, \dot{V}_{7} \\ \dot{I}_{7} \\ \dot{V}_{9} \\ \dot{I}_{9} \end{array} \right] \; \cdots \; (16) \end{eqnarray}
この行列の要素はすべて既知(\(\rm{F}_C\) と \(\rm{F}_D\) の要素)なので, 式(10), (16) より, 端子対 \(m=1, 2, 3\) と 端子対 \(m=7, 9\) における電流・電圧の関係は以下のように表されます.
\begin{eqnarray} \left[ \begin{array} \, \dot{V}_{1} \\ \dot{I}_{1} \\ \dot{V}_{2} \\ \dot{I}_{2} \\ \dot{V}_{3} \\ \dot{I}_{3} \end{array} \right] \, = \, \left[ \begin{array}{cccccc} \, \dot{F}_{v1v4} & \dot{F}_{v1i4} & \dot{F}_{v1v5} & \dot{F}_{v1i5} \\ \dot{F}_{i1v4} & \dot{F}_{i11i4} & \dot{F}_{i1v5} & \dot{F}_{i1i5} \\ \dot{F}_{v2v4} & \dot{F}_{v2i4} & \dot{F}_{v2v5} & \dot{F}_{v2i5} \\ \dot{F}_{i2v4} & \dot{F}_{i2i4} & \dot{F}_{i2v5} & \dot{F}_{i2i5} \\ \dot{F}_{v3v4} & \dot{F}_{v3i4} & \dot{F}_{v3v5} & \dot{F}_{v3i5} \\ \dot{F}_{i3v4} & \dot{F}_{i3i4} & \dot{F}_{i3v5} & \dot{F}_{i3i5} \end{array} \right] \, \left[ \begin{array}{cccc} \, \dot{F}_{v6v7} & \dot{F}_{v6i7} & 0 & 0 \\ \dot{F}_{i6v7} & \dot{F}_{i6i7} & 0 & 0 \\ 0 & 0 & \dot{F}_{v8v9} & \dot{F}_{v8i9} \\ 0 & 0 & \dot{F}_{i8v9} & \dot{F}_{i8i9} \end{array} \right] \, \left[ \begin{array} \, \dot{V}_{7} \\ \dot{I}_{7} \\ \dot{V}_{9} \\ \dot{I}_{9} \end{array} \right] \; \cdots \; (17) \end{eqnarray}
まとめ
以上, n端子対回路網の Z行列, S行列, F行列の導出と縦続接続についてでした.


非常に勉強になりました.
Z行列とF行列の一般的な変換式を探したのですが見つけることができなかったため,参考文献があれば記載していただけると大変助かります.
コメントありがとうございます。昔どこかで一般式を見たような気がするのですが、思い出せませんでした。適当なことを言ってしまい、本当に申し訳ありません。
少し探してみたのですが、以下のリンクでは、4×4のZ行列を4×4のF行列に変換する計算が記載されています。これを一般化すれば良いのだろうと思います。
https://www.jstage.jst.go.jp/article/toyotakosenkiyo/43/0/43_KJ00006748484/_pdf/-char/ja