分布定数回路におけるS行列とは?S⇔Z行列相互変換とS行列の活用
本サイトではこれまで, 「Z行列」や「F行列」など, 回路の接続計算を簡単にする行列について紹介してきました.
今回紹介するのは, 分布定数回路の測定や高周波測定で使われる行列表現, 「S行列(Sパラメータ)」です.
本稿では,
- S行列とは何か?
- S行列を他の行列表現(Z行列や F行列)と相互変換する方法
- S行列はどういう場面で使われるのか?
について解説します.
目次
2端子対回路網と分布定数回路
S行列を理解するには, Z行列などの 2端子対回路網の知識と, 分布定数回路における電信方程式(伝送線路方程式)の知識, 双方が必要です.
まずは, Z行列の復習から始めます.
2端子対回路網
1本の線に見える電源ケーブルの中には「行き」と「帰り」の2本の導線が存在し, 「行き」と「帰り」を流れる電流は, 大きさが同じで向きが反対になっています.
電源ケーブルのプラグのように, 流れる電流の大きさが同じで向きが反対になっている2つの端子の組が「端子対」です. 端子対は電気回路の中に多数散見されます.
電源ケーブルであれば, 片方がコンセントに繋がっている場合, もう片方は負荷(PC 等の電化製品)に繋がっていることが一般的でしょう.
電源に繋がっている端子対は「入力端子対」, 負荷に繋がっている端子対は「出力端子対」と呼ばれます.
電源ケーブルにはこれ以外に端子対はありませんので, 2つの端子対(4つの端子)における電流と電圧の入出力が, 電源ケーブルという回路網における入出力のすべてです.
このように2つの端子対で囲まれた回路網を「2端子対回路網」または「4端子回路網」と呼びます.
Z行列
2端子対回路網の実用上重要な点は, 「2端子対回路網を構成する要素がすべて線形素子であれば, その電気的性質を \( 2 \times 2 \) の行列で表すことができる」ということです.
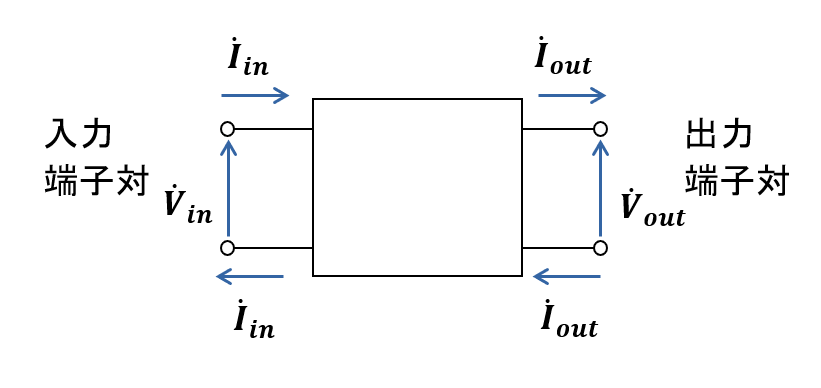
とある 2端子対回路網に対する入出力電圧・電流が 図1 のように与えられている場合, 電流と電圧の関係を表す \( 2 \times 2 \) の行列 Z が 1つに定まります.
\begin{eqnarray} \left[ \begin{array} \, \dot{V}_1 \\ \dot{V}_2 \end{array} \right] \, = \, Z \, \left[ \begin{array} \, \dot{I}_1 \\ \dot{I}_2 \end{array} \right] \end{eqnarray}
この行列 Z の成分は, 全て単位が \( [ \Omega ] \) であるため, インピーダンス行列, または, Z行列と呼ばれます.
詳細は省きますが, 任意の回路網における Z行列を求めるにあたって, 回路の中身を把握する必要はありません. 回路に対する入出力電圧・電流を計測すれば, 回路を構成する要素がどんなものであっても(線形素子で構成されていることさえ既知ならば), Z行列を決定することができます.
つまり, 回路の構成要素が全く分からないブラックボックスであっても, Z行列を求めることができるのです.
また, Z行列が既知の回路網があれば, 入力が分かった段階で, 出力を1つに定めることができます.
2端子対回路網や Z行列について詳しくは以下をご参照ください.
分布定数回路と電信方程式
続きまして, 分布定数回路の話です.
分布定数回路とは高周波を扱うケーブルや, 電線, 海底ケーブルなど, 「『部品サイズ』と『電流(もしくは電圧)の波長』が同程度の大きさ」となる電気部品を扱うための考え方です.
分布定数回路においては, 高校までに習っていた回路(集中定数回路と呼ぶ)と違って, 回路部品は空間に薄く広く分布しています.
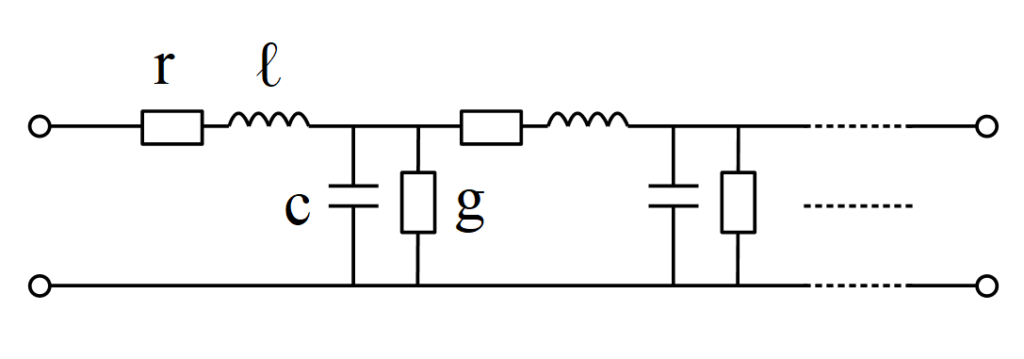
分布定数回路内の電圧 \( \dot{V} (x) \) , 電流 \( \dot{I} (x) \) は以下のように記述されます.
\begin{eqnarray} \left\{ \begin{array} \, \frac{ \mathrm{d} ^2}{ \mathrm{d} x^2} \, \dot{V} (x) = \dot{\gamma} ^2 \, \dot{V} (x) \\ \, \frac{ \mathrm{d} ^2}{ \mathrm{d} x^2} \, \dot{I} (x) = \dot{\gamma} ^2 \, \dot{I} (x) \end{array} \right. \; \cdots \; (2) \\ \rm{ } \\ \rm{ } \, \left( \dot{\gamma} ^2 = \dot{z} \dot{y} \right) \end{eqnarray}
式(2) を電信方程式, または, 伝送線路方程式と呼びます.
ここで, \( \dot{z} =r + j \omega \ell \), \( \dot{y} = g + j \omega c \), \(j\) は虚数単位, \( \omega \) は入力電圧信号の角周波数, \(r, \ell, c, g \) はそれぞれ単位長さあたりの抵抗, インダクタンス, キャパシタンス, コンダクタンスです. 回路要素はすべて単位長さ当たりの値になります.
また, \( \dot{\gamma} \) は減衰定数と呼ばれ, 波が単位長さを進んだときに, どれだけ減衰するかを表します.
導出方法, 意味するところの詳細については以下のリンクをご参照ください.
分布定数回路内の入射波と反射波
電信方程式 (2) の一般解は以下のように表せます.
\begin{eqnarray} \left\{ \begin{array} \, \dot{V} (x) &=& \dot{A} e^{- \dot{\gamma} x} \, + \, \dot{B} e^{ \dot{\gamma} x} \\ \, \dot{I} (x) &=& \dot{z}_0 ^{-1} \; \left( \dot{A} \, e^{- \dot{\gamma} x} \, – \, \dot{B} e^{ \dot{\gamma} x} \right) \end{array} \right. \; \cdots \; (3) \\ \rm{ } \\ \rm{ } \, \left( \dot{z}_0 = \sqrt{ \dot{z} / \dot{y} } \right) \end{eqnarray}
電圧も電流も 2つの項の和で表されていて, \( \dot{A} e^{- \dot{\gamma} x} \) の項を入射波, \( \dot{B} e^{ \dot{\gamma} x} \) の項を反射波と呼びます. また, \( \dot{z}_0 \) は特性インピーダンスと呼ばれます.
入射波と反射波は時刻に対して進む方向が逆向きです. 反射波は分布定数回路の特性や, 回路に接続された負荷とのインピーダンス差によって生じます.
つまり, これを逆に使えば, 反射波を解析することによって, 接続された負荷の特性を調べることができるわけです. これが今回の S行列の話に繋がってきます.
分布定数回路のS行列
ここからやっと S行列の話に移ります.
S行列とは
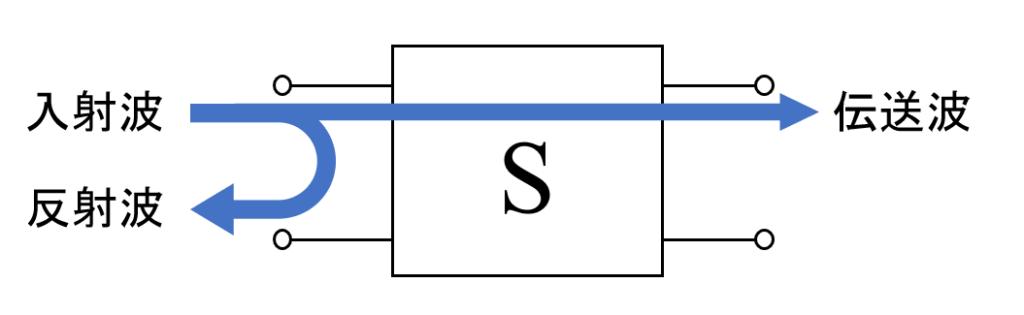
S行列とは回路網(特に分布定数回路)の行列表現です.
回路網をブラックボックスとし, 入出力のみを考えようとする点では, S行列と他の行列表現( Z行列や F行列)は共通しています.
S行列が他の行列表現と異なるのは, 「何を入出力とするのか」という点です.
Z行列や F行列では電流や電圧を入出力として考えましたが, S行列では「入射波と反射波」を入出力とします.

入射波の組 \( \left[ \begin{array}{cc} \; \dot{a}_{1} \\ \; \dot{a}_{2} \end{array} \right] \) と, 反射波の組 \( \left[ \begin{array}{cc} \; \dot{b}_{1} \\ \; \dot{b}_{2} \end{array} \right] \) の関係は
\begin{eqnarray} \left[ \begin{array} \, \dot{b}_1 \\ \dot{b}_2 \end{array} \right] \, = \, \left[ \begin{array}{cc} \, \dot{S}_{11} & \dot{S}_{12} \\ \, \dot{S}_{21} & \dot{S}_{22} \end{array} \right] \, \left[ \begin{array} \, \dot{a}_1 \\ \dot{a}_2 \end{array} \right] \; \cdots \; (4) \end{eqnarray}
のように表すことができ, \( S = \left[ \begin{array}{cc} \, \dot{S}_{11} & \dot{S}_{12} \\ \, \dot{S}_{21} & \dot{S}_{22} \end{array} \right] \) を S行列と呼びます.
式(4) を用いると, S行列の要素はそれぞれ以下のように表されます.
\begin{eqnarray} \left\{ \begin{array} \, \dot{S}_{11} = \frac{\dot{b}_1}{\dot{a}_1} \Big{|} _{\dot{a}_{2} = 0} \\ \, \dot{S}_{12} = \frac{\dot{b}_1}{\dot{a}_2} \Big{|} _{\dot{a}_{1} = 0} \\ \, \dot{S}_{21} = \frac{\dot{b}_2}{\dot{a}_1} \Big{|} _{\dot{a}_{2} = 0} \\ \, \dot{S}_{22} = \frac{\dot{b}_2}{\dot{a}_2} \Big{|} _{\dot{a}_{1} = 0} \end{array} \right. \; \cdots \; (5) \end{eqnarray}
S行列とZ行列の関係
S行列と Z行列は入出力が異なるだけで, 同じ回路網を見ています. F行列と Z行列が相互に変換できたように, S行列と Z行列も相互変換可能です. 実際に変換してみましょう.
準備として, まず, 式(3) を少し変形し, 対称的で見やすい式にします.
\begin{eqnarray} \left\{ \begin{array} \, \dot{V} (x) &=& \dot{z}_0 ^{1/2} \; \left( \dot{A} e^{- \dot{\gamma} x} \, + \, \dot{B} e^{ \dot{\gamma} x} \right) \\ \, \dot{I} (x) &=& \dot{z}_0 ^{-1/2} \; \left( \dot{A} e^{- \dot{\gamma} x} \, – \, \dot{B} e^{ \dot{\gamma} x} \right) \end{array} \right. \; \cdots \; (6) \end{eqnarray}
式(3) と 式(6) は \( \dot{A} \) と \( \dot{B} \) が表すものが違うだけで, 全く同じ意味です.
\( x = x_{1} \) における電圧, 電流, 特性インピーダンスをそれぞれ \( \dot{V}_{1}, \dot{I}_{1}, \dot{z}_{1} \) とします. \( \dot{a}_{1} = \dot{A} e^{- \dot{\gamma} x_{1}}, \dot{b}_{1} = \dot{B} e^{- \dot{\gamma} x_{1}} \) なので,
\begin{eqnarray} \left\{ \begin{array} \, \dot{V}_{1} &=& \dot{z}_1 ^{1/2} \; \left( \dot{a}_{1} + \dot{b}_{1} \right) \\ \, \dot{I}_{1} &=& \dot{z}_1 ^{-1/2} \; \left( \dot{a}_{1} \, – \, \dot{b}_{1} \right) \end{array} \right. \; \cdots \; (7) \end{eqnarray}
と表せます.
式(7) は図3 の左側の各物理量の関係を表しており, 図3 中右側の関係式も同様にして求めることができます.
\begin{eqnarray} \left\{ \begin{array} \, \dot{V}_{2} &=& \dot{z}_2 ^{1/2} \; \left( \dot{a}_{2} \, + \, \dot{b}_{2} \right) \\ \, \dot{I}_{2} &=& \dot{z}_2 ^{-1/2} \; \left( \dot{a}_{2} \, – \, \dot{b}_{2} \right) \end{array} \right. \; \cdots \; (8) \end{eqnarray}
式(7) と式(8) では \(+x\) の方向が逆向きであることにご注意ください.
式(7) と 式(8)から S行列を求めるため, \( \dot{V}, \dot{I}, \dot{a}, \dot{b} \) の関係をまとめます.
\begin{eqnarray} \begin{cases} \left[ \begin{array} \, \dot{V}_1 \\ \dot{V}_2 \end{array} \right] \, = \, \left[ \begin{array}{cc} \, \sqrt{ \dot{z}_1 } & 0 \\ \, 0 & \sqrt{ \dot{z}_2 } \end{array} \right] \, \left( \left[ \begin{array}{cc} \, \dot{a}_1 \\ \, \dot{a}_2 \end{array} \right] \, + \, \left[ \begin{array}{cc} \, \dot{b}_1 \\ \, \dot{b}_2 \end{array} \right] \right) \, \\ \, \rm{ } \\ \left[ \begin{array} \, \dot{I}_1 \\ \dot{I}_2 \end{array} \right] \, = \, \left[ \begin{array}{cc} \, 1/ \sqrt{ \dot{z}_1 } & 0 \\ \, 0 & 1/ \sqrt{ \dot{z}_2 } \end{array} \right] \, \left( \left[ \begin{array}{cc} \, \dot{a}_1 \\ \, \dot{a}_2 \end{array} \right] \, – \, \left[ \begin{array}{cc} \, \dot{b}_1 \\ \, \dot{b}_2 \end{array} \right] \right) \end{cases} \; \cdots \; (9) \end{eqnarray}
\( U= \, \left[ \begin{array}{cc} \, \sqrt{ \dot{z}_1 } & 0 \\ \, 0 & \sqrt{ \dot{z}_2 } \end{array} \right] \), \( V = \, \left[ \begin{array}{cc} \, 1/ \sqrt{ \dot{z}_1 } & 0 \\ \, 0 & 1/ \sqrt{ \dot{z}_2 } \end{array} \right] \) を使って書き換えると,
\begin{eqnarray} \begin{cases} \left[ \begin{array} \, \dot{a}_1 \\ \dot{a}_2 \end{array} \right] \, = \, \frac{1}{2} V \, \left[ \begin{array} \, \dot{V}_1 \\ \dot{V}_2 \end{array} \right] \, + \, \frac{1}{2} U \, \left[ \begin{array} \, \dot{I}_1 \\ \dot{I}_2 \end{array} \right] \\ \rm{ } \\ \, \left[ \begin{array} \, \dot{b}_1 \\ \dot{b}_2 \end{array} \right] \, = \, \frac{1}{2} V \, \left[ \begin{array} \, \dot{V}_1 \\ \dot{V}_2 \end{array} \right] \, – \, \frac{1}{2} U \, \left[ \begin{array} \, \dot{I}_1 \\ \dot{I}_2 \end{array} \right] \end{cases} \; \cdots \; (10) \end{eqnarray}
Z行列を用いれば, \( \left[ \begin{array} \, \dot{V}_1 \\ \dot{V}_2 \end{array} \right] \, = \, Z \, \left[ \begin{array} \, \dot{I}_1 \\ \dot{I}_2 \end{array} \right] \) と表されるため,
\begin{eqnarray} \begin{cases} \left[ \begin{array} \, \dot{a}_1 \\ \dot{a}_2 \end{array} \right] \, = \, \frac{1}{2} \, \left( VZ \, + \, U \right) \, \left[ \begin{array} \, \dot{I}_1 \\ \dot{I}_2 \end{array} \right] \\ \rm{ } \\ \, \left[ \begin{array} \, \dot{b}_1 \\ \dot{b}_2 \end{array} \right] \, = \, \frac{1}{2} \, \left( VZ \, – \, U \right) \, \left[ \begin{array} \, \dot{I}_1 \\ \dot{I}_2 \end{array} \right] \end{cases} \; \cdots \; (11) \end{eqnarray}
式(11) より,
\begin{eqnarray} \, \left[ \begin{array} \, \dot{b}_1 \\ \dot{b}_2 \end{array} \right] \, &=& \, \frac{1}{2} \, \left( VZ \, – \, U \right) \, \left[ \, \frac{1}{2} \, \left( VZ \, + \, U \right) \right] ^{-1} \, \left[ \begin{array} \, \dot{a}_1 \\ \dot{a}_2 \end{array} \right] \\ \rm{ } \\ \, \left[ \begin{array} \, \dot{b}_1 \\ \dot{b}_2 \end{array} \right] \, &=& \, \left( VZ \, – \, U \right) \, \left( VZ \, + \, U \right) ^{-1} \, \left[ \begin{array} \, \dot{a}_1 \\ \dot{a}_2 \end{array} \right] \; \cdots \; (12) \end{eqnarray}
よって, \( S = \left( VZ \, – \, U \right) \, \left( VZ \, + \, U \right) ^{-1} \) のように Z行列を用いて S行列を表すことができました.
S ⇔ Z行列の相互変換
式(12) を用いることで, Z行列を S行列に変換できるわけですが, もちろん逆も可能です. S行列を用いて Z行列を表してみましょう.
まずは S行列を整理します.
\begin{eqnarray} S &=& \left( VZ \, – \, U \right) \, \left( VZ \, + \, U \right) ^{-1} \\ &=& \left( VZ \, – \, U \right) \, V \, V^{-1} \left( VZ \, + \, U \right) ^{-1} \\ &=& \left( VZV \, – \, E \right) \, \left( VZV \, + \, E \right) ^{-1} \; \; \left( E=UV : 単位行列 \right) \; \cdots \; (13) \end{eqnarray}
S行列を更に変形して, \( Z= \cdots \) という形を目指します.
\begin{eqnarray} S \, \left( VZV \, + E \right) &=& VZV \, – \, E \\ SVZV \, + \, S &=& VZV \, -\, E \\ VZV \, – \, SVZV &=& E \, + \, S \\ \left( E \, – \, S \right) \, VZV &=& E \, + \, S \\ VZV &=& \left( E \, – \, S \right) ^{-1} \, \left( E \, + \, S \right) \\ Z &=& U \, \left( E \, – \, S \right) ^{-1} \, \left( E \, + \, S \right) \, U \; \cdots \; (14) \end{eqnarray}
以上より, Z行列を S行列で表すことができました.
S行列の活用
Z行列や F行列と異なり, 入出力が「電流と電圧」でない S行列は普通の回路の計算に使うことを目的としていません.
S行列が活躍するのは「ネットワークアナライザ」という測定機器を用いて, 分布定数回路の解析をする場合です.
ネットワークアナライザは, 高周波特性(10 GHz程度まで)を調べることを目的とした測定機器です.
ネットワークアナライザでは, 測定対象に正弦波を印加し, 各端子対における電圧の振幅と位相を測定します.
\( \dot{a}_{2} = 0 \) として, 振幅と位相を測れば, 反射係数( = 反射波 / 入射波 = \( \dot{b}_{1} / \dot{a}_{1} = \dot{S}_{11} \) )と伝送係数( = 伝送波 / 入射波 = \( \dot{b}_{2} / \dot{a}_{1} = \dot{S}_{21} \) )が求められます. 反対方向にも測定を行えば, \( \dot{S}_{22} \) と \( \dot{S}_{12} \) も求められ, S行列を決定できるという仕組みです.
ネットワークアナライザで測定した結果は S行列のパラメータを使って表示されます.
インピーダンスアナライザとネットワークアナライザの測定原理の違いについては「インピーダンスの計測と計測器 (その2) – 計測器・測定器玉手箱 | ORIX Rentec Corporation(外部リンク)」をご覧ください.
Z行列ではダメなのか?
本稿で述べた通り, S行列と Z行列は相互変換できます.
であれば, 結果を Sパラメータで表示する理由はどこにあるのでしょう?測定した結果をネットワークアナライザが内部的に処理して, Zパラメータに変換すれば済む話です.
しかし, この変換をすると「原因が分からなくなる」という問題が生じます.
例えば, Sパラメータにおいては明確な違いとして認識できる数値の変化であっても, Zパラメータにすると他の要因と混ざり, 信号が埋もれて見えなくなってしまう, ということが有り得ます. 元のデータに計算処理を施すほど, 元データの持つ意味は薄れてしまう(ように見える)のです.
上述の通り, インピーダンスアナライザ(電流と電圧の測定)とネットワークアナライザ(反射波と伝送波の測定)では測定原理が異なります. よって, それぞれが『測定しているもの』をより大きく反映する表示方法を用いるべきでしょう.
その意味では, S行列 ⇔ Z行列の相互変換は, 慎重に行わなければなりません.
まとめ
今回のまとめです.
- S行列は 2端子対回路網における入射波と反射波の関係を表す行列である.
- S行列と Z行列は相互に変換できる.
- S行列はネットワークアナライザで測定した結果を表示する際に用いられる.

