変成器の仕組みと行列表現:理想変成器が生み出す論理の歪み
本稿では, 変成器の構成や仕組みについて解説していきます.
変成器は電力輸送において重要な役割を果たし, 皆様の身近にも存在する電子部品ですが, 高校では中途半端にしか学びません.
それもそのはず. 変成器をきっちり議論するのは大変です. 本稿でも厳密な取り扱いは避け, 概念的な理解に留めつつ, 最終的には変成器の行列表現を目指します.
目次
変成器とは
変成器の機能は「電圧の大きさの変換」です. 回路記号では以下のように表されます。
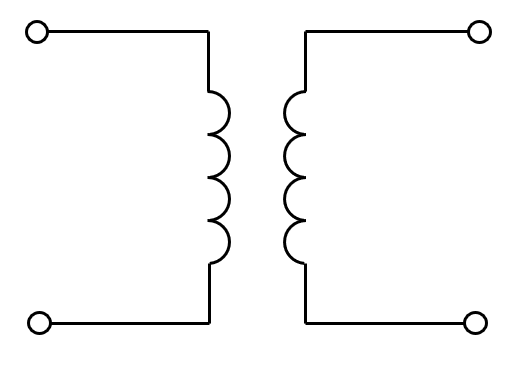
変成器にも様々種類がありますが、私たちが日常生活で最もよく目にする変成器は電柱トランスでしょう.

発電所で作られた電力は高い電圧を有します. 電柱に取り付けられている円柱状の部品(トランス)は, この電圧を下げ, 家庭用電化製品が使用できる電圧に変換します.
変成器の原理・構造
変成器とは「コイルを 2つ並べ, 磁気的に相互作用させる電子部品」です.
コイルの自己誘導と相互誘導
コイルに電流を流すと磁界を生じることは義務教育で学習されたことと思います.
電流が流れているコイルの近くに方位磁針を置くと方位磁針の向きが変わる, という実験をご覧になられたことでしょう.
また, コイルに流れる電流を変化させると, 電磁誘導によって電流の変化を妨げる向きの起電力が生じます.
コイル自身の電流変化によって電磁誘導現象が生じるため, これを「自己誘導」と呼びます.
以上がコイル 1つの場合. 以下はコイル 2つの場合です.
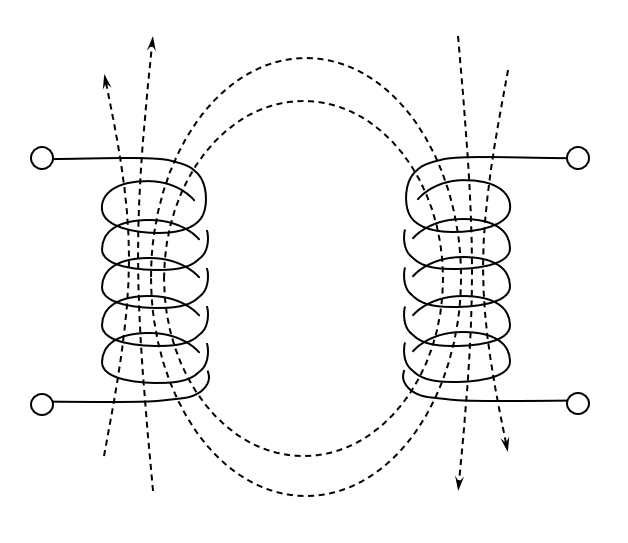
隣接して置かれた 2つのコイルの片方に電流を流す場合を考えます. 電流を直接流す方を 1次コイル, もう片方の電流を流さない方を 2次コイルと呼ぶことにしましょう.
1次コイルで生じた磁束は 2次コイル側をも貫く(鎖交する)ことがあります. このとき, 1次側コイルの電流を変化させて磁束が変化すると, 2次側コイルを鎖交する磁束も変化し, 磁束の変化によって 2次側にも誘導電圧が生じます.
これは 1次側と 2次側を入れ替えても同様です.
2つのコイルが磁界を介して相互に影響し合い, 電圧を誘起するこのような現象を「相互誘導」と呼びます.
「トランス(変成器)」は, この相互誘導を利用した装置です.
自己インダクタンスと相互インダクタンス
上述した自己誘導と相互誘導を数式で眺めてみましょう.
磁気的相互作用が無く, 単独に存在するコイルに電流を流したとき, 流れる電流 \(i\) と磁束 \(\Phi\) は以下の関係で表されます.
\begin{eqnarray} \Phi = \frac{\mu N S }{ \ell } \, i \; \cdots \; (1) \end{eqnarray}
\(\mu\) は透磁率で, \(N, S, \ell \) はそれぞれコイルの巻き数, 断面積, 長さです. なぜこうなるのかは詳しく解説すると長くなります. その辺りは電磁気の教科書をご参照ください.
式(1) の両辺を時刻 \(t\) で微分し, ファラデーの電磁誘導の法則 \(V = N \frac{d \phi}{dt}\) から電圧と電流の関係を導くと,
$$ v = \frac{\mu N^{2} S }{ \ell } \, \frac{d i}{d t} = L \, \frac{d i}{d t} \; \cdots \; (2) $$
ここで \(L\) は電流と電圧の関係を表す比例定数であり, 自己インダクタンスと呼ばれます.
次に, 2つのコイルが磁気的に結合している場合を考えます. 下付き文字はコイルの 1次側, 2次側を表します.
1次側で生じた磁束 \(\phi _1\) のうち, \(k \phi _1\) が 2次側を鎖交する(\(0<k<1\))場合, 2次側の鎖交磁束(\(\phi_2=k\phi_1\))と起電力の関係は,
\begin{eqnarray} v_{2} &=& N_{2} \, \frac{d \phi _{2}}{dt} \\ \rm{ } \\ &=& k N_{2} \, \frac{d \phi _{1}}{dt} \; \cdots \; (3) \end{eqnarray}
式(1), (3) より, 1次側の電流 \(i_1\) と2次側の電圧 \(v_2\) について, 以下の式が導かれます.
\begin{eqnarray} v_{2} \, &=& \, k N_{2} \, \frac{\mu _{1} N_{1} S_{1} }{ \ell _{1} } \, \frac{d i_{1} }{d t} \\ \rm{ } \\ \, &=& \, \frac{ k \mu_{1} N_{1} N_{2} S_{1} }{ \ell _{1} } \, \frac{d i_{1} }{d t} \, = M \, \frac{d i_{1} }{d t} \; \cdots \; (4) \end{eqnarray}
この \(M\) を相互インダクタンスと呼びます.
相互インダクタンスの定義(式(4))を見ると, コイルの長さ, 太さ, 内部の透磁率が同じ場合, 1次コイルと 2次コイルで電流を流すコイルを入れ替えても \(M\) は同じ値になることが分かります.
このとき, 式(2), (4)より
\begin{eqnarray} M= k \sqrt{ L_{1} \, L_{2} } \; \cdots \; (5) \end{eqnarray}
が成り立ちます.
また, \( k \) は 1次側で生じた磁束のうち, 2次側に鎖交する磁束の割合を表したものでした. 1次側で生じた磁束のすべてが 2次側に鎖交する場合は \(k=1\) となり, 1次側と 2次側に磁気的相互作用が全くない場合に \(k=0\) となります.
則ち, \(k\) とは 2つのコイルの磁気的結合度合いを示す定数であり, 結合定数と呼ばれます.
式(2) と 式(4) をまとめると, 長さと太さが同じコイルが 2つ並んでいて, 両者ともに電流が流れているとき, 各電流と電圧の関係は以下のように表されます.
\begin{eqnarray} \left\{ \begin{array} \, v_{1} &=& L_{1} \, \frac{di_{1}}{dt} \, + \, M \, \frac{di_{2}}{dt} \\ \, v_{2} &=& M \, \frac{di_{1}}{dt} \, + \, L_{2} \, \frac{di_{2}}{dt} \end{array} \right. \; \cdots \; (6) \end{eqnarray}
変成器の様々な表示方法
交流回路におけるフェーザ表示
1次側コイルに流れる電流が正弦波交流であれば, 2次側に流れる電流や電圧も正弦波であり, 周波数も同じなので, 複素数表示(フェーザ表示)することができます.
式(6) をフェーザ表示してみましょう.
\begin{eqnarray} \left\{ \begin{array} \, \dot{V}_{1} &=& j \omega L_{1} \, \dot{I}_{1} \, + \, j \omega M \, \dot{I}_{2} \\ \, \dot{V}_{2} &=& j \omega M \, \dot{I}_{1} \, + \, j \omega L_{2} \, \dot{I}_{2} \end{array} \right. \; \cdots \; (7) \end{eqnarray}
ここで, \(j\) は虚数単位, \(\omega\) は角周波数です. フェーザ表示について詳しくは以下の記事をご参照ください.
フェーザ表示の方が計算が簡単なので, 以下ではフェーザ表示で話を進めます.
変成器の等価回路表現
1次側, 2次側に流れる電流と電圧についての一般式(7) は以下のように変形できます.
\begin{eqnarray} \left\{ \begin{array} \, \dot{V}_{1} &=& j \omega \, ( L_{1} \, – \, M ) \, \dot{I}_{1} \, + \, j \omega M \, ( \dot{I}_{1} \, + \, \dot{I}_{2} ) \\ \, \dot{V}_{2} &=& j \omega M \, ( \dot{I}_{1} \, + \, \dot{I}_{2} ) \, + \, j \omega \, ( L_{2} \, – \, M ) \, \dot{I}_{2} \end{array} \right. \; \cdots \; (8) \end{eqnarray}
式(8) が表している電流と電圧の関係は, 下の図の3つのコイルからなる回路と等価です.
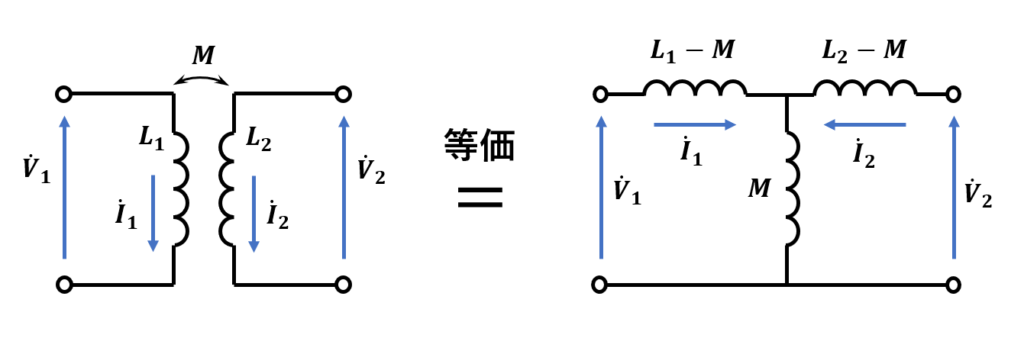
変成器はこのような等価回路で置き換えることができます.
変成器の行列表現
上述の通り, 変成器は 3つのコイルのみからなる回路と等価であり, コイルは線形素子なので, 変成器も線形素子です.
そして, 線形素子であれば, 4端子回路網を用いた行列表現ができます.
行列表現とは何ぞや?という方は以下のリンクをご参照ください.
変成器の Z行列と F行列を求めてみます.
まずは Z行列から求めていきますが, 実は Z行列は既に求めています. 変成器に対する入出力電流・電圧の関係式 (7) は Z行列そのものです.
$$ \left[ \begin{array} \, \dot{V}_{1} \\ \, \dot{V}_{2} \end{array} \right] = \left[ \begin{array}{cc} j \omega L_{1} & j \omega M \\ j \omega M & j \omega L_{2} \end{array} \right] \, \left[ \begin{array} \, \dot{I}_{1} \\ \, \dot{I}_{2} \end{array} \right] \; \cdots \; (9) $$
続いて, Z行列を使って F行列を求めます.
$$ \left[ \begin{array} \, \dot{V}_{1} \\ \, \dot{I}_{1} \end{array} \right] = \left[ \begin{array}{cc} L_{1} \, / \, M & \omega \, \left( L_{1} L_{2} \, – \, M^{2} \right) \, / \, j \omega \\ 1 \, / \, j \omega M & L_{2} \, / \, M \end{array} \right] \, \left[ \begin{array} \, \dot{V}_{2} \\ \, – \dot{I}_{2} \end{array} \right] \; \cdots \; (10) $$
F行列導出完了です. Z行列と F行列を変換するときには \(\dot{I}_{2}\) の向きにご注意下さい.
理想変成器
理想変成器とは
1次側で発生した磁束が 2次側を鎖交せず, どこか別のところに飛んで行ってしまうと, 周囲の電子部品に影響を与えますし, 電力のロスに繋がります.
それを避けるためには, 発生した磁束の全てが 2次側をも鎖交することが「理想」です.
ではどうすれば理想的な変成器を作ることができるでしょうか?
一般的には, 透磁率がとても大きな「鉄心」を両コイル内部に貫通させます. 2つのコイルを鉄心に巻き付けたような構造の変成器を作ると, 互いのコイルで生じた磁束のほとんどは, もう一方のコイルをも鎖交します.
透磁率とは, 磁束の流れやすさとでも言いましょうか. 電気回路の導電率に相当するものが磁気回路における透磁率です. 電子が導電率の高い(抵抗の低い)場所を通りたがるのと同じように, 磁束は透磁率が高い場所を通りたがります.
また, 電力ロスが生じないことが「理想」ですので, コイル自体の抵抗や, 鉄心における損失も可能な限り小さくします.
磁気特有の現象として, 磁気飽和やヒステリシスなどという面倒なものも本来は考えねばなりませんが, この辺りも限りなく小さくすることが可能です.
上記を満たすと, 結合定数は \(k \simeq 1\) となり, このような変成器を「理想変成器」と呼びます.
\(k=1\) のとき, 相互インダクタンスと自己インダクタンスは \(M^{2} = L_{1} \, L_{2} \) の関係を有します.
理想変成器の F行列
理想変成器の F行列を求めてみましょう.
上述した通り, 理想変成器において, 透磁率 \(\mu\) は べらぼうに大きな数( \(= \infty\))で, 結合定数 \(k=1\) です. これを F行列の式に突っ込んでいきます.
まず, \(M^{2} = L_{1} \, L_{2} \) であることから,
$$ n= M \, / \, L_{1} = L_{2} \, / \, M = N_{2} \, / \, N_{1} \; \cdots \; (11) $$
と置くと, 式(10) は, \(n\) を用いて以下のように変形できます.
$$ F = \left[ \begin{array}{cc} 1 \, / \, n & 0 \\ 1 \, / j \omega M & n \end{array} \right] \; \cdots \; (12) $$
また, 透磁率 \(\mu = \infty\) であるため, \(M \, ( \, = \, \frac{k \mu N_{1} N_{2} S}{ \ell } \, )\) はとても大きな数になり, \(\frac{1}{j \omega M} \simeq 0\) です.
以上まとめると, 理想変成器の F行列は
$$ F = \left[ \begin{array}{cc} \, 1 \, / \, n \, & \, 0 \, \\ \, 0 \, & \, n \, \end{array} \right] \; \cdots \; (13) $$
となります.
変成器の場合は, F行列を使って書くよりも, 連立方程式の形にして書く方が分かりやすいでしょう. つまりこういうことです.
\begin{eqnarray} \left\{ \begin{array} \, \dot{V}_{2} \, &=& \, n \, \dot{V}_{1} \, \\ \, \dot{I}_{2} \, &=& \, \frac{1}{n} \, \dot{I}_{1} \, \end{array} \right. \; \cdots \; (14) \end{eqnarray}
理想変成器は, コイルの巻数比 \(n\) に応じて, 電圧や電流を変換する装置であることが分かります.
このとき, \(\dot{V}_{1} \times \dot{I}_{1}\) と \(\dot{V}_{2} \times \dot{I}_{2}\) は等しく, 1次側と2次側で電力は変化しない(変成器は電力を消費しない)ことが分かります.
補足:理想変成器の Z行列
ここからは蛇足として「理想変成器の Z行列」についても考えてみたいと思います.
導出方法は F行列の場合と同じです.
\(\mu = \infty\), \(k=1\) を使って, 一般の変成器の Z行列を書き換えるだけ. だけなのですが. . .
$$ Z = \left[ \begin{array}{cc} \, 0 \, & \, 0 \, \\ \, 0 \, & \, 0 \, \end{array} \right] \; \cdots \; (15) $$
F行列と同じ方法で導出したにも関わらず, おかしなことになってしまいました. 式(15) の Z行列は理想変成器が持つ性質(電圧変換, 電流変換)を正しく表現していません.
また, F行列と Z行列を相互に変換することも不可能です. Z行列は理想変成器を表現する方法として適切ではないことが分かります.
このような「歪み」を生んだのは, 「理想変成器」の「理想」の部分です.
これまで理想変成器を単純化して理解するために, 行列の成分を近似し, \(0\) にしたことが何度もありました. しかし, ここは本来 \(0\) ではなく, 「\(0\) と見做せる微小量」です. ここを \(0\) にせず, 「微小だとしても存在する値」のまま計算を進めれば, F行列と Z行列の変換が正しく実行できます.
「分かりやすさ」を追求し, 微小なものを「些事」として無視することで「厳密性の破綻」という歪みが生じたわけです.
まとめ
以上, 変成器についてでした.
厳密に考え出すと何かと大変ですが, 理想変成器が持つ機能は大変シンプルです.
理想変成器はコイルの巻数に応じて, 電圧を \(n\)倍, 電流を \(1/n\) 倍します.
本稿では行列を使って理想変成器の特徴を述べましたが, 理想変成器を導出する方法は他にもたくさんありますので, 1つの方法程度に捉えて頂ければよいかと.

